Por Wikipedia

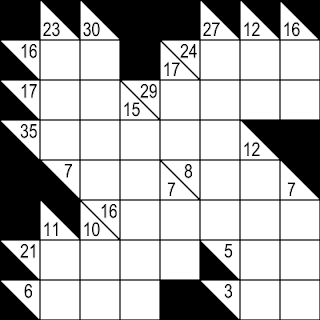
O kakuro é um jogo de raciocínio lógico. A palavra, de origem japonesa, resulta da palavra adição com a palavra inglesa cross, que em português significa cruzar. Este quebra-cabeça é visto como a transliteração matemática das palavras cruzadas, sendo por isso conhecido também pelo nome somas cruzadas.

Regras:

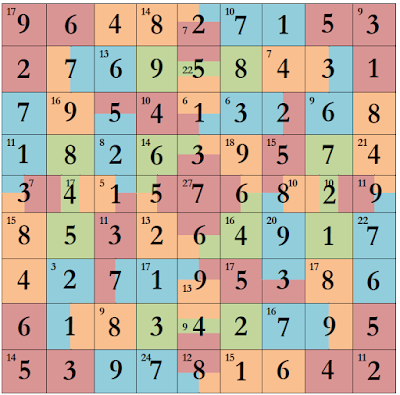
Quebra-cabeça: abaixo, temos um exemplo de um kakuro nível fácil.



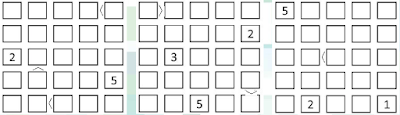
Solução: a solução para este quebra-cabeça está indicado a seguir.



Por Dan Katz

Futoshiki é um quebra-cabeça japonês cujo significado é "desigualdade". É baseado no quadrado latino, contendo restrições do tipo "é-maior-que" entre as células, com seu respectivo símbolo matemático (>). Observe as restrições nos três quadrados; ao contrário de um futoshiki típico (composto por apenas um quadrado latino), nenhum dos três quadrados pode ser resolvido de forma independente. Desde que o sudoku tornou-se popular, matemáticos e jogadores de quebra-cabeças têm se interessado em sudokus com o mínimo de dicas possível. Um estudo semelhante para o futoshiki, onde as dicas podem ser números ou desigualdades, conduziram a muitas questões interessantes em aberto.

Muitos exemplos de futoshiki podem ser encontrados na Internet; na Wikipedia, por exemplo, há um artigo em inglês sobre esse quebra-cabeça (vide aqui). Para uma perspectiva matemática, estão postados aqui alguns slides da minha palestra sobre futoshiki que apresentei no Joint Mathematics Meetings de 2012.

Instruções:

Sobre o autor: Dan Katz é conferencista da Universidade Brown. Este artigo saiu na revista MAA Focus, edição de Jun/Jul - 2012.

Solução deste quebra-cabeça: abaixo temos a solução para o futoshiki triplo proposto.



Por Robert Fuhrer

O quebra-cabeça ken-ken é uma diversão familiar em muitas publicações ao redor do mundo, sítios na web e ainda em aplicações móveis. Também são utilizados por mais de 30.000 professores em suas aulas para ensinar habilidades matemáticas, raciocínio lógico, solução de problemas, pensamento criativo e perseverança. Neste artigo, iremos um passo além para explorar algumas variações interessantes do jogo.

Regras básicas do ken-ken:

Veja o exemplo abaixo:

Quebra-cabeça 1: O quebra-cabeça abaixo é um ken-ken 9 x 9 que segue as regras padrões, mas representa um desafio real!





Por Sonia Brown, Jim Henle, Christine Niccoli e Bayla Weick



Por sudoku "vazio" queremos dizer que não existem dicas com números. Temos muitas variantes deste quebra-cabeça e apresentamos três delas. Em todos os sudokus apresentados aqui, os números 1, 2, 3, 4 e 5 tem que aparecer em cada linha e coluna. No quebra-cabeça à esquerda, a soma dos números em cada uma das regiões em destaque deve ser a mesma.

No quebra-cabeça do meio, a soma dos números em cada uma das regiões em destaque deve ser diferente. Finalmente, no quebra-cabeça à direita, a soma dos números em cada uma das regiões em destaque tem que resultar num número primo. Quebra-cabeças do primeiro tipo foram introduzidos alguns anos atrás no artigo "Creating clueless puzzles", da autoria de Jerry Butters, Fred Henle, Jim Henle e Colleen McGaughey no The Mathematical Intelligencer.



Sobre os autores: Sonia Brown, Jim Henle, Christine Niccoli e Bayla Weick são estudantes universitários na faculdade Smith, Northampton, Massachusetts. Este artigo saiu na MAA Focus, Jun/Jul - 2013.

Solução do quebra-cabeça: abaixo, a solução apresentada pelos autores para este tipo de sudoku.



Há dois desafios neste quebra-cabeça: (1) encontre um caminho que viaje da entrada até a saída; e (2) identifique o matemático utilizado como base para o labirinto.

Por David Shoenthal

Algumas variantes de sudoku negociam os dígitos iniciais no quebra-cabeça por informação alternativa, tal como a soma ou o produto de dígitos em uma região. Nesta variante, temos somas de dígitos em regiões sobrepostas.

Regras:

O teorema das quatro cores estabelece que qualquer mapa plano pode ser colorido usando-se apenas quatro cores, de tal modo que duas regiões não compartilhem nem uma fronteira não-trivial nem a mesma cor. Sua primeira conjectura foi escrita por Arthur Cayley em seu artigo de 1879: "On the colourings of maps", mas a conjectura original foi feita por Francis Guthrie. Ele coloriu um mapa da Inglaterra usando apenas quatro cores e pergunto-se se esse resultado se aplicaria a qualquer mapa. Em 2002 um trabalho conjunto feito por Maria Chudnovsky, Neil Robertson, Paul Seymour e Robin Thomas, que pode ser visto aqui, provam o teorema gráfico perfeito forte, que relaciona os tipos de gráficos para os quais pode-se resolver este tipo de problema de colorização em geral.

Sobre o autor: David Shoenthal é chefe de cadeira e um professor associado da Universidade Longwood. Este artigo saiu na revista MAA Focus, na edição de Dez - 2011/Jan - 2012.

Solução deste quebra-cabeça: abaixo temos a solução deste sudoku a quatro cores.

Por Jérôme Morin-Drouin

Com Alcazar, meu objetivo foi criar um quebra-cabeça que requer menos paciência e mais pensamento criativo que quebra-cabeças com números. Um sudoku sem números, como gosto de dizer. Cada nível apresenta uma sala que você tem que visitar:

Com regras tão simples, qualquer um consegue apreciá-lo. Assim, à medida que a dificuldade aumenta, o jogo revela qualidades que vão além das minhas expectativas iniciais. Após centenas de níveis, nossa pequena comunidade de jogadores sempre encontra meios novos e inesperados de resolver cada quebra-cabeça. Você pode encontrar muitas dessas técnicas no blog do jogo.

Apenas recentemente um talentoso jogador de Alcazar percebeu que muitas das estratégias do jogo podem ser derivadas de uma fórmula simples que eu pomposamente chamo de teorema fundamental do Alcazar: pegue qualquer quebra-cabeça Alcazar e pinte seus quadrados como em um tabuleiro de xadrez. Seja Qp o conjunto de quadrados pretos e Qb o conjunto de quadrados brancos. Escolha qualquer região R ⊆ Qp ∪ Qb. Suponha que a solução para o jogo cruze a fronteira R, np + nb vezes: np é o número de vezes que ele sai de R por um quadrado preto (“saída preta”) e nb o número de vezes que ele sai de R por um quadrado branco (“saída branca”). Temos:

2(| R ∩ Qb |) - (| R ∩ Qp |) = nb - np

Em outras palavras, em qualquer parte do quebra-cabeça Alcazar, o número adicional de saídas pretas é duas vezes o número adicional de quadrados pretos. Por exemplo, qualquer retângulo com um número par de quadrados tem que ter a mesma quantidade de quadrados pretos e brancos. Mas primeiro, a melhor forma de apreciar o jogo é encontrar você mesmo as técnicas de solução, sem fórmulas. Vá em frente e tente! Diga-me o que você acha visitando meu site. Lá, você encontrará muitas formas de continuar jogando em papel, Android, iOS e outros. Divirta-se com mais estes três desafios:

Desafio fácil:

Solução dos quebra-cabeças: abaixo temos a solução para cada Alcazar proposto.

Desafio fácil:

Desafio médio:



Desafio difícil: