|
| O Parthenon, templo grego dedicado à deusa Atenas, construído entre 447 e 438 a.C. na cidade de Atenas, Grécia. |
Euclides afirma, na definição 3 do Livro V do Elementos, que:
Uma razão (logos) é um tipo de relação associado ao tamanho entre duas magnitudes do mesmo tipo.
E na definição 6 introduz uma terminologia alternativa, ao dizer:
Sejam [quatro] magnitudes que tenham a mesma razão às quais denominemos proporcionais (analogon)...
Razão consiste, basicamente, na comparação de tamanhos entre dois termos e proporção é uma combinação de razões. Como todos os conceitos matemáticos, estes dois evoluíram conforme a civilização. Entre os árabes, al-Qalasadi expressava proporção da seguinte forma:
$$ 144\therefore 84\therefore 12\therefore 7 $$
Em 1.631, o matemático inglês William Oughtred usava um ponto para identificar razão e quatro pontos para indicar uma proporção:
$$ 144.84::12.7 $$
Em 1.790, o matemático português José Anastácio da Cunha usava a letra d na horizontal para indicar uma razão, e os quatro pontos para a proporção. Nos dias de hoje, a razão é indicada como:
$$ \frac{144}{84} $$
Que nada mais é que a nossa velha conhecida fração; e a proporção é representada como uma comparação entre duas ou mais frações:
$$ \frac{144}{84}=\frac{12}{7} $$
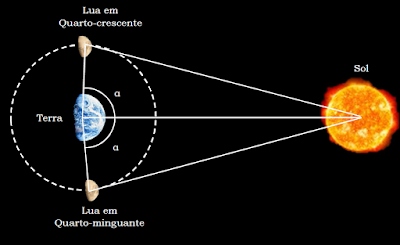
Um das mais antigas e interessantes aplicações da proporção é atribuída ao matemático e astrônomo grego Aristarco de Samos (310 a.C. a 230 a.C.), que através de um método genial foi capaz de calcular qual a proporção existente entre a distância da Terra à Lua em relação à distância da Terra ao Sol. Já foi comentado no segundo volume desta série – no capítulo da potenciação – que Aristarco, ao contrário de Arquimedes, considerava que a Terra girava ao redor do Sol. Ele também considerava que a Lua girava ao redor da Terra. Além disso, este notável sábio constatou que a Lua posicionava-se praticamente acima de sua cabeça, quando ela se encontrava nas fases de quarto-crescente ou quarto-minguante, exatamente ao nascer ou ao pôr-do-sol, conforme o esquema abaixo:
Se nas condições citadas a Lua encontra-se quase
acima de nossas cabeças, então o ângulo α formado pela abertura entre a linha que separa
a Terra do Sol e a linha que separa a Terra da Lua (tanto no quarto-crescente
quanto no quarto-minguante) corresponde a um valor muito próximo a 1/4 do
círculo que a Lua percorre ao redor da Terra, ou seja, 90 graus. Como bons
astrônomos, os antigos gregos eram perspicazes o bastante para saberem o tempo
gasto pela Lua para dar uma volta completa ao redor da Terra, o chamado ciclo lunar, que é de:
$$ 29\frac{1}{2}\mathrm{dias}=\frac{59}{2}\mathrm{dias} $$
E que o tempo consumido para que a Lua mude de fase, passando de quarto-crescente para quarto-minguante é, em média, de:
$$ 14\frac{1}{4}\mathrm{dias}=\frac{49}{4}\mathrm{dias} $$
Este valor tem 1 dia a menos que o tempo que a Lua consome para passar de quarto-minguante para quarto-crescente. A soma do tempo gasto entre as duas mudanças de fase resulta:
$$ 14\frac{1}{4}+15\frac{1}{4}\Rightarrow \frac{57}{4}+\frac{61}{4}=\frac{118}{4}=\frac{59}{2}=29\frac{1}{2}\mathrm{dias} $$
Assim, a proporção utilizada na linha de raciocínio de Aristarco foi esta: se um ciclo lunar (ou seja, se o tempo para a Lua dar uma volta completa, ou percorrer os 360 graus no círculo orbital ao redor da Terra) demora 29½ dias, então a abertura no círculo orbital equivalente a 2α graus corresponderá aos 14¼ dias que a Lua consome entre o quarto-crescente e o quarto-minguante:
$$ \frac{360}{29\frac{1}{2}}=\frac{2\alpha }{14\frac{1}{4}}\Rightarrow \frac{360}{\frac{59}{2}}=\frac{2\alpha }{\frac{57}{4}} $$
Multiplicando ambas as razões por um mesmo número, mantemos a igualdade inalterada. Se esse número for uma multiplicação entre os denominadores das razões, obtemos:
$$ \frac{360}{\frac{59}{2}}\times \left ( \frac{59}{2}\times \frac{57}{4} \right )=\frac{2\alpha }{\frac{57}{4}}\times \left ( \frac{59}{2}\times \frac{57}{4} \right ) $$
Como temos apenas multiplicações e divisões, os 59/2 no numerador da razão à esquerda da igualdade podem ser simplificados com os 59/2 no denominador da mesma razão. Igual procedimento pode ser adotado para os 57/4 da razão à direita da igualdade. Obtém-se:
$$ 360\times \frac{57}{4}=2\alpha \times \frac{59}{2} $$
Efetuando as multiplicações, resulta:
$$ \frac{360\times 57}{4\times 59}=\alpha $$
Onde obtemos:
$$ \frac{20.520}{236}=\alpha $$
Finalmente, simplificando a fração resultante, chega-se a uma abertura angular α no círculo orbital da Lua ao redor da Terra de:
$$ \frac{20.520}{236}=\frac{10.260}{118}=\frac{5.130}{59}\rightarrow \alpha =86\frac{56}{59}\cong 86,95graus $$
De posse do valor da abertura angular é possível estimar a distância relativa da Terra ao Sol, definindo-se uma distância relativa da Terra à Lua; com uma régua, desenhe um segmento de reta de 1 cm de comprimento, saindo do centro da Terra até o centro da Lua. Com a ajuda de um transferidor, ajuste o ângulo de inclinação desse segmento de reta para 87 graus, que é muito próximo dos 86,95 graus calculados. Desenhando segmentos de reta perpendiculares às superfícies da Terra e da Lua que se afastem em direção a um ponto comum distante de ambas, a intersecção dos segmentos será o centro do Sol, conforme se observa na figura abaixo:
Se tudo foi desenhado corretamente, a distância da Terra ao Sol estará situada entre 18 e 20 cm, cujo valor absoluto foi aquele encontrado por Aristarco, ou seja, proporcionalmente o Sol dista 20 vezes mais que a Lua em relação à Terra. Atualmente, sabe-se que a razão entre a distância do Sol à Terra em relação à distância da Terra à Lua é cerca de 400 em valor absoluto, quer dizer:
$$ \frac{Distância-Sol-Terra}{Distância-Terra-Lua}\cong 400 $$
O que faz com que o ângulo de inclinação da Lua em relação a um observador na Terra seja de 89,86 graus e não de 86,95 graus; essa diferença de cálculo, entretanto, não tira o mérito de Aristarco, ao contrário, prova que o astrônomo grego seguiu uma linha de raciocínio corretíssima, um feito notável para alguém que viveu há mais de 2.200 anos atrás! Conhecer as distâncias que separam os astros tinha, e tem até hoje, uma importância maior à nossa sobrevivência que propriamente saciar as curiosidades; o excerto abaixo – tirado do livro Dom Quixote, de Miguel de Cervantes (obra publicada pela primeira vez em 1.605) – demonstra a importância do estudo dos astros para a agricultura:
[...] Pedro (o pastor) respondeu que o que sabia era que o morto era um fidalgo rico, que morava numa aldeia naquelas serras, que tinha sido estudante muitos anos em Salamanca, voltando para casa com fama de muito sábio e muito lido.
– Diziam que sabia principalmente a ciência das estrelas, e do que fazem lá no céu o sol e a lua, porque pontualmente nos dizia as clipes do sol e da lua.
– Eclipse, amigo, não clipes, se chama o obscurecimento desses dois astros maiores – disse dom Quixote.
Mas Pedro, não reparando em ninharias, prosseguiu sua história:
– Também adivinhava quando o ano seria abundante ou estíl.
– Quereis dizer estéril, amigo – disse dom Quixote.
– Estéril ou estíl – respondeu Pedro – sai tudo pelo mesmo lugar. E digo que seu pai e seus amigos, que acreditavam nele, ficaram muito ricos, porque faziam o que ele aconselhava: “Semeai cevada este ano, não trigo; neste podeis semear grãos-de-bico e não cevada; o ano que vem vai abarrotar de azeitona; nos três seguintes não se colherá um fiapo”.
– Essa ciência se chama astrologia – disse dom Quixote. [...]
De fato, desde a pré-história o ser humano olha para o céu, estudando o movimento dos astros e das estrelas, relacionando esses objetos e seus movimentos a fenômenos como a chuva, a seca, as estações do ano e as marés.
Para reduzir a razão 12/15 à unidade, é preciso multiplicá-la por 15/12; mas, para manter a proporção parcial, a razão 31/23 também deve ser multiplicada por 15/12:
Seguiremos o mesmo raciocínio para a fração resultante com a próxima razão à sua direita. Teremos:
Para reduzir à unidade a razão à esquerda, mantendo a proporção parcial entre ambas as frações, procede-se conforme segue:
Repetimos o processo para a próxima dupla de razões:
Novamente, busca-se reduzir à unidade a razão à esquerda, mantendo-se a proporção parcial na razão à direita:
Restam-nos, agora, duas razões e o problema reduz-se a uma regra de três simples:
Desta vez, interessa-nos isolar a quantidade que se deseja descobrir (indicada pelo ponto de interrogação), ou seja, quantos barcelonenses valem 15 imperiais; para isso, é mais fácil multiplicar ambas as razões por 12:
Obtemos, enfim:
Que é o mesmo resultado obtido simplificadamente pela multiplicação em cruz de Fibonacci, ou seja, 15 imperiais valem 20 barcelonenses, mais 1180/3289 centavos de barcelonense. Do exposto, nota-se que as regras de três simples e composta foram uma ferramenta quantitativa de grande importância no século XIII. No comércio de especiarias, por exemplo, fica claro que os mercadores que não fossem capazes de calcular os valores relativos entre os produtos negociados, ou conseguiam fazê-los apenas de modo aproximado ou com dificuldade, estavam em clara desvantagem nas negociações e nas trocas. De modo análogo essas regras mostram sua utilidade e importância no câmbio monetário; ao tempo de Fibonacci, a Itália tinha a maior concentração de moedas, com 28 diferentes cidades-estados cunhando suas moedas – 7 apenas na região da Toscana – todas baseadas no sistema romano de valoração: denari, soldi, lire. Antes do Liber Abaci, o câmbio entre diferentes moedas era feito com o ábaco. Com a introdução do sistema hindu-arábico, as casas de câmbio certamente modificaram e aprimoraram a maneira de modelar e analisar os valores relativos entre múltiplas moedas rapidamente. Não é à toa que, mais de 800 anos após sua introdução na Europa, a regra de três ainda é amplamente utilizada no comércio, feiras livres, quitandas, etc., para calcular o valor de um produto ou mercadoria cujo peso, volume ou metragem seja proporcional (para mais ou para menos) ao valor de um peso, volume ou metragem de referência.
Este valor tem 1 dia a menos que o tempo que a Lua consome para passar de quarto-minguante para quarto-crescente. A soma do tempo gasto entre as duas mudanças de fase resulta:
$$ 14\frac{1}{4}+15\frac{1}{4}\Rightarrow \frac{57}{4}+\frac{61}{4}=\frac{118}{4}=\frac{59}{2}=29\frac{1}{2}\mathrm{dias} $$
Assim, a proporção utilizada na linha de raciocínio de Aristarco foi esta: se um ciclo lunar (ou seja, se o tempo para a Lua dar uma volta completa, ou percorrer os 360 graus no círculo orbital ao redor da Terra) demora 29½ dias, então a abertura no círculo orbital equivalente a 2α graus corresponderá aos 14¼ dias que a Lua consome entre o quarto-crescente e o quarto-minguante:
$$ \frac{360}{29\frac{1}{2}}=\frac{2\alpha }{14\frac{1}{4}}\Rightarrow \frac{360}{\frac{59}{2}}=\frac{2\alpha }{\frac{57}{4}} $$
Multiplicando ambas as razões por um mesmo número, mantemos a igualdade inalterada. Se esse número for uma multiplicação entre os denominadores das razões, obtemos:
$$ \frac{360}{\frac{59}{2}}\times \left ( \frac{59}{2}\times \frac{57}{4} \right )=\frac{2\alpha }{\frac{57}{4}}\times \left ( \frac{59}{2}\times \frac{57}{4} \right ) $$
Como temos apenas multiplicações e divisões, os 59/2 no numerador da razão à esquerda da igualdade podem ser simplificados com os 59/2 no denominador da mesma razão. Igual procedimento pode ser adotado para os 57/4 da razão à direita da igualdade. Obtém-se:
$$ 360\times \frac{57}{4}=2\alpha \times \frac{59}{2} $$
Efetuando as multiplicações, resulta:
$$ \frac{360\times 57}{4\times 59}=\alpha $$
Onde obtemos:
$$ \frac{20.520}{236}=\alpha $$
Finalmente, simplificando a fração resultante, chega-se a uma abertura angular α no círculo orbital da Lua ao redor da Terra de:
$$ \frac{20.520}{236}=\frac{10.260}{118}=\frac{5.130}{59}\rightarrow \alpha =86\frac{56}{59}\cong 86,95graus $$
De posse do valor da abertura angular é possível estimar a distância relativa da Terra ao Sol, definindo-se uma distância relativa da Terra à Lua; com uma régua, desenhe um segmento de reta de 1 cm de comprimento, saindo do centro da Terra até o centro da Lua. Com a ajuda de um transferidor, ajuste o ângulo de inclinação desse segmento de reta para 87 graus, que é muito próximo dos 86,95 graus calculados. Desenhando segmentos de reta perpendiculares às superfícies da Terra e da Lua que se afastem em direção a um ponto comum distante de ambas, a intersecção dos segmentos será o centro do Sol, conforme se observa na figura abaixo:
Se tudo foi desenhado corretamente, a distância da Terra ao Sol estará situada entre 18 e 20 cm, cujo valor absoluto foi aquele encontrado por Aristarco, ou seja, proporcionalmente o Sol dista 20 vezes mais que a Lua em relação à Terra. Atualmente, sabe-se que a razão entre a distância do Sol à Terra em relação à distância da Terra à Lua é cerca de 400 em valor absoluto, quer dizer:
$$ \frac{Distância-Sol-Terra}{Distância-Terra-Lua}\cong 400 $$
O que faz com que o ângulo de inclinação da Lua em relação a um observador na Terra seja de 89,86 graus e não de 86,95 graus; essa diferença de cálculo, entretanto, não tira o mérito de Aristarco, ao contrário, prova que o astrônomo grego seguiu uma linha de raciocínio corretíssima, um feito notável para alguém que viveu há mais de 2.200 anos atrás! Conhecer as distâncias que separam os astros tinha, e tem até hoje, uma importância maior à nossa sobrevivência que propriamente saciar as curiosidades; o excerto abaixo – tirado do livro Dom Quixote, de Miguel de Cervantes (obra publicada pela primeira vez em 1.605) – demonstra a importância do estudo dos astros para a agricultura:
[...] Pedro (o pastor) respondeu que o que sabia era que o morto era um fidalgo rico, que morava numa aldeia naquelas serras, que tinha sido estudante muitos anos em Salamanca, voltando para casa com fama de muito sábio e muito lido.
– Diziam que sabia principalmente a ciência das estrelas, e do que fazem lá no céu o sol e a lua, porque pontualmente nos dizia as clipes do sol e da lua.
– Eclipse, amigo, não clipes, se chama o obscurecimento desses dois astros maiores – disse dom Quixote.
Mas Pedro, não reparando em ninharias, prosseguiu sua história:
– Também adivinhava quando o ano seria abundante ou estíl.
– Quereis dizer estéril, amigo – disse dom Quixote.
– Estéril ou estíl – respondeu Pedro – sai tudo pelo mesmo lugar. E digo que seu pai e seus amigos, que acreditavam nele, ficaram muito ricos, porque faziam o que ele aconselhava: “Semeai cevada este ano, não trigo; neste podeis semear grãos-de-bico e não cevada; o ano que vem vai abarrotar de azeitona; nos três seguintes não se colherá um fiapo”.
– Essa ciência se chama astrologia – disse dom Quixote. [...]
De fato, desde a pré-história o ser humano olha para o céu, estudando o movimento dos astros e das estrelas, relacionando esses objetos e seus movimentos a fenômenos como a chuva, a seca, as estações do ano e as marés.
 |
| O Newgrange, monumento pré-histórico localizado na Irlanda, construído em torno de 3.200 a.C., durante o período Neolítico. O monumento está alinhado com o sol nascente do solstício de inverno. |
Entre os romanos, o uso de proporções pode ser devidamente apreciado no trabalho de Marcos Vitrúvio Polião (no latim: Marcus Vitruvius Pollio), arquiteto que viveu no século 1 a.C. e que deixou como legado a obra De Architectura ("Os dez livros de arquitetura"), único tratado do período greco-romano que chegou aos nossos dias e que influenciou no Renascimento diversos textos sobre arquitetura, urbanismo, hidráulica e engenharia. No livro III, capítulo I – Do projeto e simetria de templos – Vitrúvio comenta:
"O projeto de templos depende da simetria, as regras nas quais os arquitetos deveriam mais cuidadosamente observar. Simetria deriva de proporção, que os gregos denominam 'analogia'. Proporção é uma função de ajuste entre os ta-manhos das diferentes partes, umas em relação às outras e em relação ao todo; deste ajuste apropriado depende a simetria. Por isso, nenhuma construção poderá ser considerada como bem construída sem que se queira simetria e proporção. Em verdade, elas são tão necessárias à beleza de uma construção como o são em uma figura humana bem formada, que a Natureza tenha tão bem modelado, que a face, do queixo ao topo da testa, ou às raízes do cabelo, equivalha à décima parte da altura do corpo inteiro. Do queixo ao topo da cabeça, à oitava parte do corpo inteiro, e da nuca ao topo da cabeça, o mesmo. Da parte superior do peito às raízes do cabelo, um sexto; ao topo da cabeça, um quarto. Uma terça parte da altura do rosto é igual àquela do queixo à parte inferior das narinas, e daí ao meio das sobrancelhas o mesmo; a partir do último para as raízes do cabelo, onde termina o topo da cabeça, a restante terça parte. O comprimento do pé é a sexta parte da altura do corpo. O antebraço, uma quarta parte. A largura do peito, uma quarta parte. Similarmente têm os outros membros suas devidas proporções, em atenção às quais os antigos pintores e escultores obtiveram tanta reputação. Assim também as partes dos templos deveriam corresponder umas às outras e com o todo. O umbigo é naturalmente posicionado no centro do corpo humano, e, se a um homem deitado com o rosto para cima, com suas mãos e pés esticados, tendo seu umbigo como centro, for desenhado um círculo, este tocará os dedos das mãos e dos pés. Não é somente por um círculo que o corpo humano está circunscrito, já que ele pode ser posicionado dentro de um quadrado. Ao medir-se dos pés ao topo da cabeça, e depois ao longo dos braços totalmente estendidos, encontramos a última medida igual à anterior; de modo que linhas em ângulos retos umas às outras, fechando a figura, formarão um quadrado. Se a Natureza, portanto, fez o corpo humano de tal sorte que seus diferentes membros são as medidas do todo, então os antigos, com grande propriedade, determinaram-nas em todos os trabalhos perfeitos, em que cada parte seria uma alíquota do todo; e uma vez que eles estabelecem que isto seja observado em todas as obras, mais estritamente devem ser observados nos templos dos deuses, em que as falhas, bem como as belezas, perduram até ao fim dos tempos.”
As especificações do corpo humano estabelecidas por Vitrúvio, comparando as diferentes partes proporcionalmente em relação ao todo, permitiu a Da Vinci elaborar o seu famoso "Homem Vitruviano", obra que abre o capítulo da divisão, no primeiro volume desta série:
Veja que na base do desenho existe uma marcação, como uma régua, utilizada por da Vinci para respeitar as medidas das proporções defendidas por Vitrúvio para aquilo que o arquiteto romano concebia como um corpo humano perfeito. Observe, por exemplo:
"... a face, do queixo ao topo da testa, ou às raízes do cabelo, equivale à décima parte da altura do corpo inteiro."
Neste caso, temos:
$$ Altura-queixo-cabelo=\frac{Altura-do-corpo}{10} $$
Isto não quer dizer que outras proporções encontradas nos corpos humanos, próximas (ou não tão próximas) daquelas apontadas por Vitrúvio deixem de apresentar a beleza e a harmonia das partes em relação ao todo, mas as observações do arquiteto demonstram o conceito de beleza que os romanos herdaram dos gregos e do uso que efetivamente faziam dele nas artes e na arquitetura das construções. Muito antes dos gregos e dos romanos, os egípcios já trabalhavam com razões e proporções. O papiro de Ahmes apresenta o seguinte problema relacionado ao tema:
“Tijoleiro, tenho pressa em erguer esta casa. Hoje não há nuvens e não preciso de muito mais tijolos, para a qual tenho todos de que necessito, exceto 300. Tu sozinho em um dia os produziria todos, mas vosso filho pára de trabalhar quando chega aos 200 e teu genro quando chega aos 250. Trabalhando juntos, em quantos dias conseguis produzí-los?”
Para resolvê-lo, primeiro os egípcios davam um "chute" para a quantidade necessária de dias para produzir os 300 tijolos, por exemplo, 1 dia. Em seguida, somavam a quantidade de tijolos que cada tijoleiro produziria em 1 dia: 300 do pai, mais 200 do filho e outros 250 do genro, totalizando 750 tijolos. Como o chute inicial está acima da quantidade necessária de tijolos, os egípcios lançavam mão de um artifício geométrico denominado "falsa posição" (cujo nome em latim é regula falsa, que traduzido para o português resulta em: falsa regra) que aplica semelhança de triângulos e que utiliza dois triângulos retângulos para chegar à resposta, como ilustrado abaixo:
Neste esquema, as bases AC e AE dos triângulos ABC e ADE correspondem às quantidades de tijolos e as alturas BC e DE correspondem às quantidades de dias para produzí-los. Como o chute inicial de 1 dia está acima do tempo necessário para fabricar os 300 tijolos, então a altura DE (que é maior) representará esse 1 dia e a altura BC (que é menor) representará o tempo necessário para a produção dos 300 tijolos. Por outro lado, a base AE (maior) representa o total de tijolos produzidos em um dia (750) e a base AC (menor) a quantidade desejada (300). Assim, por semelhança de triângulos, a razão entre as bases é proporcional à razão entre as alturas, ou seja:
$$ \frac{750}{300}tijolos=\frac{1}{?}dias $$
Lê-se: 750 tijolos estão para 300 tijolos (razão) assim como (proporção) 1 dia está para a quantidade de dias que se quer descobrir (razão). A igualdade indica que as frações resultam em um mesmo número racional. Agora, para simplificarmos as razões desta proporção, multiplicamos ambas as frações pelo produto dos denominadores, um procedimento que já conhecemos:
$$ \frac{750\times \left ( 300\times ? \right )}{300}=\frac{1\times \left ( 300\times ? \right )}{?} $$
Simplificando:
$$ 750\times ?=1\times 300 $$
Dividindo ambos as razões da proporção por 750 tijolos, vem:
$$ \frac{750\times ?}{750}=\frac{1\times 300}{750} $$
Simplificando os termos, tem-se:
$$ ?=\frac{300}{750}dias $$
Simplificando a fração por 30:
Simplificando a fração por 30:
$$ ?=\frac{10}{25}dias $$
Simplificando novamente a fração por 5, chega-se a:
Simplificando novamente a fração por 5, chega-se a:
$$ ?=\frac{2}{5}dia $$
Ou seja, em 2/5 de um dia os três tijoleiros, juntos, produzem os 300 tijolos que faltam para construir a casa. O nome falsa posição se deve ao 'chute' inicial que é dado como resposta preliminar ao problema. A resposta correta é obtida ajustando-se, através da proporcionalidade, o resultado esperado com aquele obtido através do chute inicial. A regra da falsa posição pode ser considerada um caso particular da regra de três simples; de fato, o mesmo problema poderia ser apresentado da seguinte forma:
“Se três tijoleiros juntos produzem 750 tijolos em um dia, quantos dias serão necessários para produzirem 300 tijolos?”
E a regra de três simples seria colocada desta forma:
Ou seja, em 2/5 de um dia os três tijoleiros, juntos, produzem os 300 tijolos que faltam para construir a casa. O nome falsa posição se deve ao 'chute' inicial que é dado como resposta preliminar ao problema. A resposta correta é obtida ajustando-se, através da proporcionalidade, o resultado esperado com aquele obtido através do chute inicial. A regra da falsa posição pode ser considerada um caso particular da regra de três simples; de fato, o mesmo problema poderia ser apresentado da seguinte forma:
“Se três tijoleiros juntos produzem 750 tijolos em um dia, quantos dias serão necessários para produzirem 300 tijolos?”
E a regra de três simples seria colocada desta forma:
$$ 750\left ( tijolos \right )\rightarrow 1\left ( dia \right ) $$
$$ 300\left ( tijolos \right )\rightarrow ?\left ( dia \right ) $$
A solução do problema é obtida multiplicando-se os termos em cruz:
$$ 300\left ( tijolos \right )\rightarrow ?\left ( dia \right ) $$
A solução do problema é obtida multiplicando-se os termos em cruz:
Em seguida, isolamos a quantidade necessária de dias para pro-duzir os tijolos, que é a informação que queremos obter, "passando" os 750 tijolos para o outro lado da igualdade; como os 750 estão multiplicando, "passam" para o outro lado dividindo:
$$ ?\left ( dia \right )=\frac{300\left ( tijolos \right )\times 1\left ( dia \right )}{750\left ( tijolos \right )}=\frac{300}{750}dia=\frac{2}{5}dia $$
Chegamos, é claro, ao mesmo resultado obtido anteriormente. Note que a maneira como calculamos em cruz e "passamos" um número de um lado para o outro da igualdade são simplificações. De fato, queimam-se algumas etapas em nome da praticidade, mas sacrifica-se o verdadeiro cálculo matemático por trás da regra de três, que é aquele apresentado na solução egípcia, onde se comparam razões proporcionais entre si. A regra de três também foi amplamente discutida e apresentada na forma de diversos problemas envolvendo transações comerciais, equivalência entre bens de consumo e câmbio monetário no Liber Abaci, de Fibonacci, como no problema proposto a seguir:
Sabendo-se que 7 rolos de pimenta valem 4 berzi e que 9 libras de açafrão valem 11 berzi, pergunta-se: quanto açafrão será adquirido com 23 rolos de pimenta?
Observe que se busca obter uma proporcionalidade, ou equivalência, entre quantidades de açafrão e pimenta em uma base monetária usada como referência, o berzi. Para chegar ao resultado, Fibonacci lança mão de um esquema, semelhante ao apresentado a seguir:
Pimenta
|
berzi
|
Açafrão
|
De início, indicamos que 7 rolos de pimenta valem 4 berzi:
Pimenta
|
berzi
|
Açafrão
|
7
|
4
|
|
Em seguida, na linha abaixo, indicamos que 9 libras de
açafrão equivalem a 11 berzi:
Pimenta
|
berzi
|
Açafrão
|
7
|
4
|
|
11
|
9
|
Por fim, queremos saber a proporção em libras de açafrão para 23 rolos de pimenta:
Pimenta
|
berzi
|
Açafrão
|
7
|
4
|
?
|
23
|
11
|
9
|
Fibonacci indica a multiplicação em cruz entre os valores da
tabela, na forma de números azuis e vermelhos, conforme segue:
Pimenta
|
berzi
|
Açafrão
|
?
|
||
23
|
11
|
9
|
Os termos azuis são multiplicados entre
si; do mesmo modo, multiplicam-se os termos vermelhos, e as
multiplicações são igualadas entre si:
$$ 7\times 11\times ?=23\times 4\times 9 $$
Executando as multiplicações em cada lado da igualdade, vem:
$$ 77\times ?=828 $$
Dividindo ambos os lados da igualdade por 77, temos:
$$ \frac{77\times ?}{77}=\frac{828}{77} $$
Chegando a:
$$ ?=\frac{828}{77} $$
Procedendo à divisão de 828/77, obtemos a fração
mista:
$$ ?=10\frac{58}{77} $$
Gerando frações unitárias a partir da fração 58/77, obtemos o equivalente em libras de açafrão para os 23 rolos de pimenta:
$$ ?=10+\frac{1}{2}+\frac{1}{4}+\frac{1}{308} $$
No caso de câmbio monetário, a proporcionalidade entre os valores de diversas moedas é ainda mais notória, como mostra o problema a seguir:
Doze imperais valem 31 pisaninos e 12 ianuínos valem 23 pisaninos e 12 turinenses valem 13 ianuínos e 12 barcelonenses valem 11 turinenses. Deseja-se saber quantos barcelonenses valem 15 imperiais.
Utilizando um esquema semelhante ao anterior para o cálculo:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
Começa-se a preencher a tabela com as associações de equivalência
entre as moedas, começando pela proporção
entre imperiais e pisaninos:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
|||
Seguindo com a proporção
entre ianuínos e pisaninos:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
|||
23
|
12
|
Preenchendo com a proporção
entre turinenses e ianuínos:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
13
|
12
|
|
23
|
12
|
Informando a proporção
entre barcelonenses e turinenses:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
13
|
12
|
|
23
|
12
|
11
|
12
|
Finalmente, posicionam-se na tabela os 15 imperiais e a
respectiva proporção que se deseja
encontrar em barcelonenses:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
13
|
12
|
?
|
15
|
23
|
12
|
11
|
12
|
Como no exemplo anterior, multiplicam-se em cruz os diversos
valores da tabela:
Imperial
|
Pisanino
|
Ianuíno
|
Turinense
|
Barcelon.
|
12
|
31
|
13
|
12
|
?
|
15
|
23
|
12
|
11
|
12
|
Os
termos azuis são multiplicados entre si; do mesmo modo, multiplicam-se
os termos vermelhos, e as multiplicações são igualadas
entre si:
$$ 12\times 23\times 13\times 11\times ?=15\times 31\times 12\times 12\times 12 $$
Dividindo-se os termos da igualdade por 12 × 23
× 13 × 11, vem:
$$ \frac{12\times 23\times 13\times 11\times ?}{12\times 23\times 13\times 11}=\frac{15\times 31\times 12\times 12\times 12}{12\times 23\times 13\times 11} $$
Fazendo as devidas simplificações, resulta:
$$ ?=\frac{15\times 31\times 12\times 12}{23\times 13\times 11}=\frac{66.960}{3.289}=20\frac{1.180}{3.289} $$
A conta de Fibonacci sem simplificação começaria assim:
$$ \frac{12}{15}=\frac{31}{23}=\frac{13}{12}=\frac{12}{11}=\frac{?}{12} $$
O objetivo aqui é reduzir a regra de três composta acima em uma regra de três simples. Para isso, reduzimos cada razão à unidade, começando da razão mais à esquerda e comparando-a com a razão à sua direita. Ao fazermos isso, vamos acumulando as proporções parciais na fração que não sofre redução à unidade. Assim, com o primeiro par de frações:
$$ \frac{12}{15}=\frac{31}{23} $$
$$ \frac{12}{15}\times \frac{15}{12}=\frac{31}{23}\times \frac{15}{12}\Rightarrow 1=\frac{31\times 15}{23\times 12} $$
$$ \frac{31\times 15}{23\times 12}=\frac{13}{12} $$
$$ \frac{31\times 15\times 23\times 12}{23\times 12\times 31\times 15}=\frac{13\times 23\times 12}{12\times 31\times 15}\Rightarrow 1=\frac{13\times 23\times 12}{12\times 31\times 15} $$
$$ \frac{13\times 23\times 12}{12\times 31\times 15}=\frac{12}{11} $$
$$ \frac{13\times 23\times 12\times 12\times 31\times 15}{12\times 31\times 15\times 13\times 23\times 12}=\frac{12\times 12\times 31\times 15}{11\times 13\times 23\times 12} $$
Simplificando, obtém-se:
$$ 1=\frac{12\times 31\times 15}{11\times 13\times 23} $$
$$ \frac{12\times 31\times 15}{11\times 13\times 23}=\frac{?}{12} $$
$$ \frac{12\times 31\times 15\times 12}{11\times 13\times 23}=\frac{?\times 12}{12} $$
$$ \frac{12\times 31\times 15\times 12}{11\times 13\times 23}=? $$