Por David Nacin

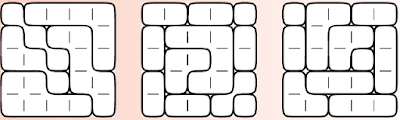
Preencha as células de modo que cada linha, coluna e caixa gradeada três-por-três contenha, exatamente e sem repetições, os números de 1 até 9. Uma linha pontilhada aparece na fronteira entre duas células se, e somente se, o número escolhido numa célula dividir sem resto o número da outra célula. Abaixo, temos uma caixa gradeada de amostra, com essa situação.

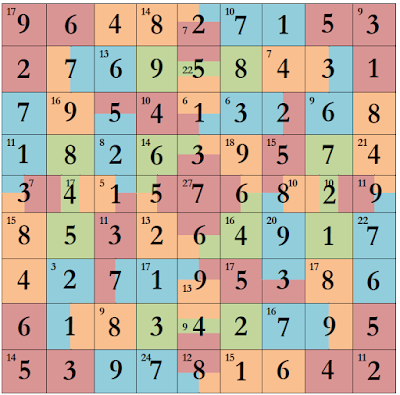
Abaixo, temos um quebra-cabeça fácil para você começar a brincar.

Uma vez que você já esteja aquecido com o jogo, tente resolver o quebra-cabeça a seguir. Divirta-se!

Sobre o autor: David Nacin é um professor na Universidade William Paterson. Este quebra-cabeça saiu na revista MAA Focus, edição de Out-2017/Nov-2017. Há outro quebra-cabeça baseado em sudoku de sua autoria divulgado neste blog. Clique aqui para conhecer.

Por David Nacin

Preencha as células de modo que cada linha, coluna e caixa gradeada três-por-três contenha, exatamente e sem repetições, cada um dos números de 1 até 9. Um quadrado indica que a média dos números contidos entre duas células adjacentes é igual a 5. Um trapézio com a base maior virada para cima indica que a média é maior que 5, e um trapézio com a base maior virada para baixo indica que a média é menor que 5.

Sobre o autor: David Nacin é um professor associado na Universidade William Paterson em Nova Jersey. Este artigo saiu na revista MAA Focus, na edição de Abr - 2017/Mai - 2017.


Solução do Média-sudoku: Da esquerda para a direita, de cima para baixo, o valor de cada célula (para cada uma das caixas gradeadas três-por-três) que fornece o correto preenchimento deste quebra-cabeça está indicado abaixo.

7-5-4-2-9-8-3-6-1
1-3-6-4-5-7-8-9-2
8-2-9-3-6-1-4-5-7
5-9-1-7-2-3-6-4-8
4-8-2-9-1-6-7-3-5
3-6-7-8-4-5-2-1-9
9-4-8-1-3-2-5-7-6
2-1-5-6-7-4-9-8-3
6-7-3-5-8-9-1-2-4

Por Lai Van Du Thinh

Posicione uma barra vertical (|), duas barras (||) ou três barras (|||) em cada uma das células vazias do tabuleiro, de modo que o número contido em uma célula iguale-se à quantidade de barras verticais nas células que circundam esse número. Além disso, a soma de barras na horizontal, na vertical ou na diagonal do tabuleiro deve ser sempre igual a 10. Não pode haver barras verticais em nenhuma célula que já contenha um número.

Sobre o autor: Lai Van Du Thinh trabalha na Munigeni Studio Game, Nha Trang, Khanh Hoa, Vietnã. Este quebra-cabeça saiu na revista Mathematics Magazine, Volume 90, No. 1, Fev-2017.

Solução do barradoku: a solução deste quebra-cabeça está indicada na figura abaixo.

Já se discutiu anteriormente sobre quebra-cabeças sudoku com um mínimo de dicas. Em 2011-2012, Gary McGuire utilizou 7 milhões de horas do tempo de supercomputação para provar por busca exaustiva que o menor número de dicas que um sudoku válido (solução única) deveria ter é 17. Para quebra-cabeças com pistas rotacionalmente simétricas, o menor número de dicas de um sudoku válido é considerado como sendo 18. Mas não estamos aqui para falar deles; hoje, daremos uma olhada nos quebra-cabeças sem nenhuma dica: o sudoku desnudo. Cada um destes quebra-cabeças veio do livro Naked Sudoku (Philip Riley/Laura Taalman), publicado pela Puzzle Wright Press. Você pode obter mais informações sobre a matemática por trás e relacionada a sudoku no livro Taking Sudoku Seriously, de Jason Rosenhouse/Laura Taalman e publicado pela Oxford University Press. Para saber mais sobre o trabalho de Gary McGuire acerca do problema do número mínimo de dicas, veja o "Sudoku Checker" no site dele. Para dar uma olhada em algumas matemáticas relativas a sudoku sendo investigadas sem computadores, tente o artigo de Elizabeth Arnold, Rebecca Field, Stephen Lucas e eu mesma, chamado: "Minimal Complete Shidoku Symmetry Groups" publicado no Journal of Combinatorial Mathematics and Combinatorial Computing (Novembro de 2013).

Quebra-cabeça 1: Sudoku-produto

Adicionando estruturas à própria grade do quebra-cabeça, pode-se fornecer informação suficiente para que não seja necessária nenhuma dica ao jogo. No sudoku-produto, as regras são as mesmas do sudoku regular (números de 1 a 9 em cada linha e coluna e blocos 3x3), mas além disso não há números repetidos em nenhuma região colorida, e os pequenos números posicionados no topo de cada região indicam qual deve ser o produto resultante dos números escolhidos para aquela região. Dica para começar: 5s e 7s são mais fáceis de poscionar na grade que outros números. Use os fatores de divisibilidade a seu favor.

Quebra-cabeça 2: Sudoku-maior-que

Neste quebra-cabeça mais uma vez damos importância efetiva à posição dos valores numéricos, mas adicionamos uma estrutura de uma maneira diferente: desta vez, indicando quais células são maiores ou menores que suas vizinhas. No sudoku-maior-que aplicam-se as regras usuais do sudoku, mas além disso os sinais de "maior que" indicam qual entre dois números vizinhos é o maior, e os símbolos triangulares "maior que" indicam que um número é mais de uma unidade maior que seu vizinho. Dicas para começar: as células rosas e azuis podem ajudá-lo a posicionar alguns 1s e 9s; a seguir, tente posicionar 2s e 8s e assim por diante.

Quebra-cabeça 3: Sudoku-divisão

Como se fosse um híbrido entre os dois quebra-cabeças anteriores, o sudoku-divisão usa símbolos para indicar quando uma célula é um divisor de seu vizinho, onde A ⊂ B siginfica que "A divide B". Algumas células também estão separadas por um sinal "maior que" para indicar que uma célula é maior que a outra. Uma pergunta de bônus: Este tipo de quebra-cabeça sempre precisará de, ao menos, um sinal "maior que". Porque isso?

Sobre a autora: Laura Taalman é editora da coluna Puzzle Page. Este artigo saiu na revista MAA Focus, na edição de Ago - 2015/Set - 2015.

Solução do Sudoku-produto: abaixo, temos a solução do primeiro quebra-cabeça proposto.

Por Sonia Brown, Jim Henle, Christine Niccoli e Bayla Weick



Por sudoku "vazio" queremos dizer que não existem dicas com números. Temos muitas variantes deste quebra-cabeça e apresentamos três delas. Em todos os sudokus apresentados aqui, os números 1, 2, 3, 4 e 5 tem que aparecer em cada linha e coluna. No quebra-cabeça à esquerda, a soma dos números em cada uma das regiões em destaque deve ser a mesma.

No quebra-cabeça do meio, a soma dos números em cada uma das regiões em destaque deve ser diferente. Finalmente, no quebra-cabeça à direita, a soma dos números em cada uma das regiões em destaque tem que resultar num número primo. Quebra-cabeças do primeiro tipo foram introduzidos alguns anos atrás no artigo "Creating clueless puzzles", da autoria de Jerry Butters, Fred Henle, Jim Henle e Colleen McGaughey no The Mathematical Intelligencer.



Sobre os autores: Sonia Brown, Jim Henle, Christine Niccoli e Bayla Weick são estudantes universitários na faculdade Smith, Northampton, Massachusetts. Este artigo saiu na MAA Focus, Jun/Jul - 2013.

Solução do quebra-cabeça: abaixo, a solução apresentada pelos autores para este tipo de sudoku.



Por David Shoenthal

Algumas variantes de sudoku negociam os dígitos iniciais no quebra-cabeça por informação alternativa, tal como a soma ou o produto de dígitos em uma região. Nesta variante, temos somas de dígitos em regiões sobrepostas.

Regras:

O teorema das quatro cores estabelece que qualquer mapa plano pode ser colorido usando-se apenas quatro cores, de tal modo que duas regiões não compartilhem nem uma fronteira não-trivial nem a mesma cor. Sua primeira conjectura foi escrita por Arthur Cayley em seu artigo de 1879: "On the colourings of maps", mas a conjectura original foi feita por Francis Guthrie. Ele coloriu um mapa da Inglaterra usando apenas quatro cores e pergunto-se se esse resultado se aplicaria a qualquer mapa. Em 2002 um trabalho conjunto feito por Maria Chudnovsky, Neil Robertson, Paul Seymour e Robin Thomas, que pode ser visto aqui, provam o teorema gráfico perfeito forte, que relaciona os tipos de gráficos para os quais pode-se resolver este tipo de problema de colorização em geral.

Sobre o autor: David Shoenthal é chefe de cadeira e um professor associado da Universidade Longwood. Este artigo saiu na revista MAA Focus, na edição de Dez - 2011/Jan - 2012.

Solução deste quebra-cabeça: abaixo temos a solução deste sudoku a quatro cores.

Por Serge C. Ballif

Um quadrado latino de ordem n é um arranjo n x n onde cada um dos n símbolos ocorre exatamente uma vez em cada linha ou coluna. Sudoku é um exemplo de quadrado latino. Dois quadrados latinos de ordem n são ditos ortogonais se cada par ordenado de símbolos ocorrer exatamente uma vez quando os quadrados forem sobrepostos. Apresentamos a seguir três sudokus que devem ser completados, sujeitos à restrição de que os quadrados de cada sudoku devem estar ortogonalmente emparelhados.

Desafio 1: Complete os dois sudokus abaixo, de tal modo que formem quadrados latinos ortogonais (Tempo limite: 6 minutos).

Desafio 2: Complete as células do pseudo-sudoku 5 x 5 abaixo, de tal modo que os dois quadrados fiquem ortogonais. Estes quadrados são denominados desenhos gerechte (Tempo limite: 10 minutos).

Desafio 3: Complete os três sudokus abaixo, de tal modo que quaisquer dois deles sejam ortogonais entre si (Tempo limite: 2 horas).

É sabido que existem no máximo seis sudokus de ordem 9 emparelhados ortogonalmente e, em geral, no máximo:

sudokus de ordem n emparelhados ortogonalmente. O leitor interessado nestes limites ou na construção de sudokus ortogonais é encorajado a ler o artigo: "Sudoku, Gerechte Designs, Resolutions, Affine Space, Spreads, Reguli and Hamming Codes", dos autores R. A. Bailey, Peter J. Cameron e Robert Connelly, que apareceu no American Mathematical Monthly 115, no. 5 (2008): 383-404.

Sobre o autor: Serge C. Ballif é um estudante graduado no departamento de matemática da Universidade estadual da Pensilvânia. Este artigo saiu na revista MAA Focus, edição de Fev/Mar - 2012.

Solução dos quebra-cabeças: abaixo temos uma solução para cada um dos desafios apresentados.

Desafio 1:

Desafio 2:

Desafio 3: