Ciência de Garagem: álgebra árabe

Pagode Ulun Danu do lago Bratan no Bali, Indonésia.

O estudo das seções cônicas auxiliaram em grande medida os primeiros estudos das equações algébricas do terceiro grau entre os árabes, pelas mãos do matemático, astrônomo e poeta persa Omar Khayyam (1.048 d.C. a 1.131 d.C.).

Um rubi acende na videira – Ilustração de 1.905 elaborada por Adelaide Hanscom Leesom para a tradução de Edward Fitzgerald do Rubayat de Omar Khayyam.

Khayyam em persa significa 'fabricante de tendas' e Omar teria adotado esse nome em memória de seu pai, que exercia esse ofício. Este brilhante matemático também é muito conhecido por sua famosa obra poética: Rubayat, que é o plural da palavra persa rubai, que significa quadras ou quartetos. Sendo um poema, o rubai consiste de quatro versos, dos quais o primeiro, o segundo e o quarto são rimados (no original) e o terceiro é branco. A poesia de Rubayat canta a existência humana, a brevidade da vida, o êxtase e o amor. Omar Khayyam desenvolveu em sua obra poética a concepção do êxtase do vinho como transcendência do homem, como se pode observar abaixo:

Rubai 5

Busca a felicidade agora, não sabes de amanhã.

Apanha um grande copo cheio de vinho,

Senta-te ao luar, e pensa:

Talvez amanhã a Lua me procure em vão.

Rubai 6

Não procures muitos amigos, nem busques prolongar

A simpatia que alguém te inspirou;

Antes de apertares a mão que te estendem,

Considera se um dia ela não se erguerá contra ti.

Rubai 7

Alcorão, o livro supremo, pode ser lido às vezes,

Mas ninguém se deleita sempre em suas páginas.

No copo de vinho está gravado um texto de adorável

Sabedoria que a boca lê, a cada vez com mais delícia.

Rubai 9

Que pobre o coração que não sabe amar

E não conhece o delírio da paixão.

Se não amas, que Sol pode te aquecer,

Ou que Lua te consolar?

Porém, Omar Khayyam foi famoso durante sua vida como matemático. Dos tratados que escreveu e que chegaram aos nossos dias temos Um comentário das dificuldades relativas aos postulados dos Elementos de Euclides, finalizado em 1.077 d.C., Da divisão de um quadrante de um círculo, sem data definida e por fim aquele que interessa a este capítulo: Das provas para problemas relativos a álgebra, este finalizado em 1.079 d.C[1]. Ele foi o primeiro a resolver geometricamente todo tipo de equação cúbica no que se refere às raízes positivas (nessa época os números negativos não eram aceitos). É no tratado de álgebra que encontraremos seus estudos sobre equações cúbicas, dividido em três partes: (i) equações que podem ser resolvidas com régua e compasso, (ii) equações que podem ser resolvidas por meio de seções cônicas e (iii) equações que envolvem o inverso da incógnita.

[1] Omar escreveu posteriormente um tratado sobre a extração da n-ésima raiz de números naturais, que infelizmente se perdeu.

Equações cúbicas e intersecção de seções cônicas – a primeira página de um manuscrito em dois capítulos, mantido na Universidade de Teerã – Irã.

Khayyam foi o primeiro matemático a classificar equações de um modo compreensivo, ainda que em termos modernos ele estivesse apenas verificando o grau de uma equação. O primeiro conjunto de equações com dois termos, ou binômios, ele as denominava equações simples, indicadas abaixo:

Binômios lineares, quadráticos e cúbicos
1.	$$ a=x $$
2.	$$ a=x^{2} $$
3.	$$ a=x^{3} $$
4.	$$ bx=x^{2} $$
5.	$$ cx^{2}=x^{3} $$
6.	$$ bx=x^{3} $$

O segundo conjunto era o que Omar denominava equações compostas, divididas em trinômios (equações com três termos) ou quadrinômios (equações com quatro termos), descritas abaixo:

Trinômios quadráticos
7.	$$ x^{2}+bx=a $$
8.	$$ x^{2}+a=bx $$
9.	$$ bx+a=x^{2} $$
Trinômios cúbicos redutíveis a equações quadráticas
10.	$$ x^{3}+cx^{2}=bx $$
11.	$$ x^{3}+bx=cx^{2} $$
12.	$$ cx^{2}+bx=x^{3} $$
Trinômios cúbicos
13.	$$ x^{3}+bx=a $$
14.	$$ x^{3}+a=bx $$
15.	$$ bx+a=x^{3} $$
16.	$$ x^{3}+cx^{2}=a $$
17.	$$ x^{3}+a=cx^{2} $$
18.	$$ cx^{2}+a=x^{3} $$
Quadrinômios em que a soma dos 3 termos é igual ao quarto termo
19.	$$ x^{3}+cx^{2}+bx=a $$
20.	$$ x^{3}+cx^{2}+a=bx $$
21.	$$ x^3+bx+a=cx^{2} $$
22.	$$ cx^{2}+bx+a=x^{3} $$
Quadrinômios em que os termos somados dois a dois igualam-se
23.	$$ x^{3}+cx^{2}=bx+a $$
24.	$$ x^{3}+bx=cx^{2}+a $$
25.	$$ x^{3}+a=cx^{2}+bx $$

Omar comenta em seu manuscrito quais equações já haviam sido anteriormente solucionadas, bem como descreve o seu método de solução de acordo com cada uma das 25 categorias de equações. Algebricamente falando, algumas destas categorias são idênticas, mas suas construções geométricas podem diferir. Em um excerto traduzido da obra de Khayyam, ele estabelece que um 'quadrado quadrado' – em linguagem moderna, o termo x⁴, é algo que “não existe na realidade de modo algum, mas sim no domínio da filosofia”. Ele continua sua explanação afirmando que “o que quer que seja obtido pela álgebra é obtido através de quatro termos: número, coisa ou raiz (x), quadrado (x²) e cubo (x³)”. A dimensionalidade fornecia a justificativa para isso, ao especificar que “número é um estado da mente independente de todas as magnitudes, não existindo na realidade”. Khayyam ia além, afirmando que “número somente vem à existência quando manifestado em alguma causa material”. Para o matemático, uma linha reta exprimia o objeto familiar aos leitores modernos como x. O quadrado, que expressamos por x², para Khayyam é “simbolizado por um quadrilátero de lados iguais e ângulos retos, cujo lado é igual à linha reta”. Finalmente, ele descrevia o cubo, que para nós seria o x³, como “um sólido limitado por seis superfícies iguais de quatro lados cada, todos os lados iguais, e com ângulos retos”. Estes quatro lados eram todos objetos do tipo linha reta (para nós, o x) e cada superfície era um quadrado (em nossa notação, o x²). Khayyam faz referência ao Elementos, de Euclides, para a construção de um cubo e afirma que “um objeto com mais de três dimensões é impossível”. De modo geral, as obras matemáticas árabes foram fortemente influenciadas pelos textos geométricos gregos, como os de Euclides, Arquimedes e Apolônio e, de modo mais específico, pela idéia de que um problema matemático não estaria totalmente solucionado sem uma prova, e estas provas eram geométricas. Por esse motivo, parte do projeto da matemática islâmica medieval foi justificar regras algébricas através da geometria, como o são as obras de Khayyam e outros matemáticos árabes, que resolveram algumas equações cúbicas propostas por Arquimedes através da intersecção de seções cônicas. Vejamos como se davam essas provas através de um dos problemas propostos por Omar Khayyam para um quadrinômio do tipo “um cubo, um quadrado e lados são iguais a um número”, ou seja:

$$ x^{3}+cx^{2}+b^{2}x=a^{3} $$

Em termos geométricos, pode-se afirmar que, dadas três quantidades substituídas por três segmentos de reta: verde, azul e vermelho, tais que possam ser representados conforme abaixo:

Todos com magnitudes conhecidas, construir um quarto segmento de reta laranja:

Cuja magnitude se deseja descobrir, tal que:

Um cubo perfeito construído com segmentos de reta laranja, somado a outro sólido cuja base é uma área com lados constituídos de segmentos de reta laranja e altura igual ao segmento de reta verde, somados a um terceiro sólido cuja base é uma área com lados constituídos de segmentos de reta azuis e altura igual ao segmento de reta laranja, forneçam uma magnitude igual ao volume do cubo cuja base é uma área com lados construídos de segmentos de reta azul e altura igual ao segmento de reta vermelho. Em termos algébricos, o somatório desses volumes é:

$$ x^{3}+cx^{2}+b^{2}x=a^{3} $$

O termo x³ (cubo para Khayyam) é o sólido laranja, o primeiro da esquerda para a direita na figura acima. A constante c corresponde à magnitude conhecida do segmento verde e o termo x² (quadrado para Khayyam) corresponde à área laranja do segundo sólido. A constante b² corresponde à área azul de magnitude conhecida do terceiro sólido e o termo x (raiz ou coisa para Khayyam) corresponde à magnitude do segmento laranja. Finalmente, a constante a³ corresponde ao sólido vermelho e azul de magnitudes conhecidas. Como a prática matemática daquele tempo insistia na manutenção da dimensionalidade, cada termo da equação polinomial era visto essencialmente como uma caixa retangular tridimensional. Assim, para Khayyam, encontrar a solução da equação cúbica reduzia-se à questão geométrica de encontrar um segmento de linha (no exemplo, o segmento laranja) a partir do qual três caixas pudessem ser construídas de tal modo que seus volumes combinados se igualassem a um volume conhecido. 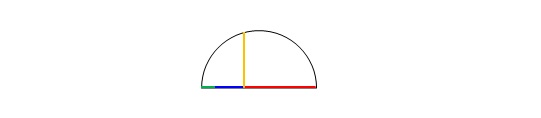A solução do matemático para este problema depende do resultado de um par de áreas iguais, uma baseada na proposição 13 do Livro VI do Elementos de Euclides, que afirma que, dados três segmentos de reta com diferentes magnitudes:

Que unidos formam o diâmetro de um semi-círculo:

E sendo esse diâmetro perpendicular a outro segmento cuja altura toca a circunferência e divide o diâmetro conforme segue:

Então, a área de um quadrilátero formado pelo segmento laranja é igual à área de outro quadrilátero formado pelos segmentos do diâmetro dispostos da seguinte forma:

O outro resultado fornecendo um par de áreas iguais vem da proposição 12 do Livro II do Cônicas de Apolônio, que estabelece uma propriedade das hipérboles, afirmando que o produto das distâncias de um ponto qualquer sobre a curva em relação às assíntotas é uma constante. Assim, dados dois pontos quaisquer A e B sobre uma hipérbole retangular, cujas assíntotas[2] estão indicadas por retas tracejadas, abaixo:

[2] Assíntota é toda reta que é tangente a uma curva no infinito. Neste caso, a curva em questão é a hipérbole. Quando as assíntotas dessa hipérbole são perpendiculares entre si, diz-se que a hipérbole é retangular.

Os quadriláteros formados pelas distâncias destes pontos às assíntotas, assim definidos:

Guardam entre si a seguinte relação de igualdade em termos de área:

Para obter essas duas áreas iguais, Khayyam arranja os segmentos verde, azul e vermelho (todos com magnitudes conhecidas) da seguinte forma:

Em seguida, o matemático desenha um semi-círculo cujo diâmetro é a soma dos segmentos verde e vermelho:

A partir do segmento azul, duas retas perpendiculares entre si são traçadas, conforme indicado abaixo:

Em seguida, uma hipérbole é construída a partir do ponto localizado na extremidade esquerda do segmento de reta vermelho. Para desenhar essa hipérbole, o segmento vermelho foi dividido em quatro partes iguais; da intersecção das retas perpendiculares, quatro linhas auxiliares são traçadas, cada uma cruzando uma divisão do segmento vermelho. Por fim, são definidos pontos de cruzamento entre essas linhas auxiliares com outras quatro linhas auxiliares horizontais, cada uma das quais é traçada a partir do encontro das linhas auxiliares que saem da interseção das retas perpendiculares com a última divisão da linha vermelha (à esquerda), conforme abaixo:

Unindo adequadamente estes cruzamentos com segmentos de reta, obtém-se uma hipérbole retangular, onde as retas perpendiculares entre si são suas assíntotas, conforme a seguir:

Para atender à proposição 12 do Livro II de Cônicas o primeiro ponto sobre a hipérbole encontra-se na extremidade esquerda do segmento de reta verde; o segundo ponto é obtido do cruzamento da hipérbole com o semi-círculo; ligando-o à assíntota vertical, obtém-se o segmento de reta laranja:

Construindo os retângulos e nomeando seus vértices, temos:

Omar Khayyam apresenta sua solução em cinco etapas, sendo que a primeira consiste em mostrar que as áreas dos retângulos DFGH e ABCD são iguais. Como comentado antes, Apolônio estabeleceu uma propriedade das hipérboles definindo que o produto das distâncias às assíntotas entre dois pontos quaisquer sobre a curva é uma constante. Uma vez que os pontos H e A estão ambos na mesma hipérbole, com assíntotas FG e BC, conclui-se que os retângulos ABEF e CEGH possuem a mesma área. Como estes dois retângulos compartilham a área CEFD, significa que os retângulos subtraídos de CEFD – ou seja, DFGH e ABCD – também possuem a mesma área.

O segundo passo consiste em desenvolver a proporção:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{\left ( EC \right )^{2}}{\left ( CD \right )^{2}} $$

Uma vez que as áreas dos retângulos DFGH e ABCD são iguais, significa que:

$$ DA\times CD=HD\times FD $$

Ou ainda, na forma de uma proporção:

$$ \frac{DA}{HD}=\frac{FD}{CD} $$

Como EC é igual a FD, então podemos alterar a proporção anterior para:

$$ \frac{DA}{HD}=\frac{EC}{CD} $$

Se as razões acima são proporcionais, então seus quadrados também o são. Assim:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{\left ( EC \right )^{2}}{\left ( CD \right )^{2}} $$

[1]

No terceiro passo, Omar faz uso do semi-círculo para obter a seginte proporção:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{DJ}{HD} $$

Como o triângulo JAH está inscrito no diâmetro de um semi-círculo, pelo teorema de Tales ele é um triângulo retângulo. Então, os triângulos DHA e DJA também são retângulos e, de fato, são semelhantes. Sendo semelhantes, vale a proporção:

$$ \frac{HD}{DA}=\frac{DA}{DJ} $$

E, portanto:

$$ \left ( DA \right )^{2}=HD\times DJ $$

Dividindo ambos os termos por (HD)², vem:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{HD\times DJ}{\left ( HD \right )^{2}} $$

Finalmente:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{DJ}{HD} $$

[2]

No quarto passo, Khayyam demonstra a seguinte relação:

$$ \left ( EC \right )^{2}\times HD=DJ\times \left ( DC \right )^{2} $$

Para chegar a esse resultado, ele combina os resultados obtidos previamente no segundo passo pela equação [1]:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{\left ( EC \right )^{2}}{\left ( CD \right )^{2}} $$

E no terceiro passo pela equação [2]:

$$ \frac{\left ( DA \right )^{2}}{\left ( HD \right )^{2}}=\frac{DJ}{HD} $$

Igualando as duas equações pelo termo comum [(DA)²/(HD)²]:

$$ \frac{\left ( EC \right )^{2}}{\left ( CD \right )^{2}}=\frac{DJ}{HD} $$

Basta multiplicar em cruz para chegar à relação desejada:

$$ \left ( EC \right )^{2}\times HD=DJ\times \left ( DC \right )^{2} $$

[3]

Khayyam interpretou este resultado como um fato geométrico em termos de sólidos geométricos, afirmando que um sólido cuja base é um quadrado com lados de magnitudes iguais a EC e altura HD terá um volume igual a outro sólido cuja base seja um quadrado com lados de magnitudes iguais a DC e altura DJ. Finalmente, no quinto e último passo, Omar verifica que a magnitude do segmento construído e denominado DC satisfaz a equação cúbica. Para chegar a essa conclusão, ele afirma que uma vez que o ponto C está entre D e J, então vale a igualdade:

$$ DC+CJ=DJ $$

[4]

Isto significa que é possível dividir uma caixa cuja base tenha uma área igual a (DC)² e altura DJ em duas caixas menores: um cubo com volume (DC)³ mais uma caixa cuja base tenha uma área igual a (DC)² e altura CJ, que combinados com a equação [3] do quarto passo fornecem:

$$ \left ( EC \right )^{2}\times HD=DJ\times \left ( DC \right )^{2} $$

$$ \left ( EC \right )^{2}\times HD=\left [ DC+CJ \right ]\times \left ( DC \right )^{2} $$

$$ \left ( EC \right )^{2}\times HD=\left ( DC \right )^{3}+CJ\times \left ( DC \right )^{2} $$

Somando agora cada lado da equação resultante com o volume:

$$ \left ( EC \right )^{2}\times DC $$

Obtemos:

$$ \left ( EC \right )^{2}\times HD+\left ( EC \right )^{2}\times DC=\left ( DC \right )^{3}+CJ\times \left ( DC \right )^{2}+\left ( EC \right )^{2}\times DC $$

$$ \left ( EC \right )^{2}\times \left [HD+DC \right ]=\left ( DC \right )^{3}+CJ\times \left ( DC \right )^{2}+\left ( EC \right )^{2}\times DC $$

Como:

$$ HD+DC=HC $$

Então:

$$ \left ( EC \right )^{2}\times HC=\left ( DC \right )^{3}+CJ\times \left ( DC \right )^{2}+\left ( EC \right )^{2}\times DC $$

[5]

Observe: EC corresponde ao segmento azul, de magnitude conhecida; HC corresponde ao segmento vermelho, cuja magnitude também é conhecida; e finalmente o segmento CJ corresponde ao segmento verde, cuja magnitude também se conhece. Logo, o segmento DC, à direita da equação [5] é o valor da incógnita e, portanto, a solução da equação de terceiro grau, correspondendo ao segmento laranja.

Se a equação de Khayyam tivesse os seguintes valores para as constantes a (segmento verde), b (segmento azul) e c (segmento vermelho) e fosse representada desta maneira:

$$ y=x^{3}+7,9x^{2}+1,3x-2,1^{3} $$

E, a partir daqui, construíssemos uma tabela de pares ordenados, escolhendo uma faixa de valores para x, tal que:

$$ x=-8, -7, ..., -1, 0, +1, ..., +10, +11 $$
e obtivéssemos os correspondentes valores para y, facilmente montaríamos um gráfico para encontrar a curva correspondente a esse polinômio, semelhante ao indicado abaixo:

A distância entre a origem do gráfico até o ponto em que a curva corta a abcissa (indicado pela seta amarela) corresponde, na prova geométrica do matemático persa, ao segmento laranja, ou incógnita, com uma magnitude tal que permite construir as caixas cujos volumes combinados se igualam. É preciso observar que essa prova geométrica valeria para qualquer outra combinação dos segmentos. Por exemplo, se permutássemos as posições dos segmentos vermelho e azul da configuração original, obteríamos um semi-círculo cujo diâmetro seria a soma das magnitudes dos segmentos verde e azul, ao invés da soma dos segmentos verde e vermelho. Como resultado uma nova hipérbole regular e um novo segmento laranja, com magnitudes diferentes da solução anterior, seriam obtidos a partir desta construção; ainda assim, a prova geométrica permaneceria válida nos termos em que foi apresentada, pois não estariam sendo violadas nem a proposição de Apolônio, nem a de Euclides, nem o teorema de Tales, mas os volumes combinados das caixas obtidas com estes novos segmentos não se igualariam. Significa dizer que apenas uma das possíveis combinações geométricas entre os segmentos verde, azul e vermelho resulta em um segmento laranja cuja magnitude é a solução da equação cúbica. Uma das equações cúbicas apresentada na obra Das provas para problemas relativos a álgebra, de Omar Khayyam, foi parar na corte de Frederico II, do Sacro Império Romano, e envolveu nosso velho conhecido Fibonacci. Depois de sua viagem de estudos à Argélia – iniciada em 1.192 – onde seu pai mantinha um entreposto comercial e diplomático na cidade de Bugia, Fibonacci publica em seu retorno a Pisa o seu monumental Liber Abacci em 1.202. Porém, em 1.225, já amplamente reputado como um grande professor de matemática e escritor, lhe é concedida uma audiência formal com o imperador Frederico II, então um patrono do saber que desejava um encontro com esse expoente em matemática da Europa. Um dos membros dessa audiência, o matemático da côrte João de Palermo, propôs três problemas para Fibonacci resolver:

1. Três homens compartilhavam libras esterlinas, não sei quantas, das quais a metade pertencia ao primeiro, um terço ao segundo e um sexto ao terceiro; como eles queriam mantê-las em um lugar seguro, cada um deles tomou das libras alguma quantia, até que nada tenha restado. O primeiro devolveu metade do que tomou, o segundo devolveu um terço e o terceiro devolveu um sexto. Quando o total devolvido foi dividido igualmente entre os três homens, percebeu-se que cada um havia recebido o que lhe era por direito. Quantas libras esterlinas havia inicialmente e quanto cada homem tomou desse montante?

2. Encontre o número racional r tal que tanto r² + 5 quanto r² – 5 sejam quadrados racionais.

3. Encontre uma raiz da equação cúbica x³ + 2x² + 10x = 20.

O primeiro problema já foi abordado anteriormente no capítulo Os números negativos, no terceiro volume desta série, e envolve uma equação linear. O segundo problema foi explicado por Fibonacci em um tratado publicado naquele mesmo ano, chamado Liber Quadratorum (Livro dos Quadrados) e envolve uma equação quadrática.

Iluminura do livro “De arte venandi cum avibus”, tratado em latim sobre ornitologia e falcoaria escrito por Frederico II em 1.240 e dedicado a seu filho Manfred. Na imagem, o imperador com um falcão.

A solução para o terceiro problema é apresentado por Fibonacci em seu manuscrito Flos (Flor, também publicado em 1.225), bem como os dois problemas anteriores, e detalha como obter a raiz da equação cúbica, que ele denomina por μ, provando que esta raiz não é um inteiro, nem um racional, nem nenhuma das outras formas apresentadas no Livro X do Elementos, de Euclides. Ou seja, trata-se de um número irracional. Nesse estudo, Fibonacci afirma: “E porque não é possível resolver esta equação por nenhum dos métodos acima, trabalhei para reduzir a solução a uma aproximação”, e por fim ele estabelece que a raiz dessa equação é, aproximadamente:
$$ \mu \cong 1; 22, 07, 42, 33, 04, 40 $$
Cuja notação sexagesimal traduzida para uma soma de frações fica:
$$ \mu \cong \frac{1}{60^{0}}+\frac{22}{60^{1}}+\frac{07}{60^{2}}+\frac{42}{60^{3}}+\frac{33}{60^{4}}+\frac{04}{60^{5}}+\frac{40}{60^{6}} $$
Em notação decimal, esta soma de frações corresponde a:
$$ \mu \cong 1,368808107\overline{85}... $$
Uma aproximação correta até a nona casa decimal! É possível que, para resolver essa equação cúbica, Leonardo de Pisa dispusesse de algum método numérico com o qual estava familiarizado. Um desses possíveis métodos é conhecido por Ruffini-Horner. Apesar do nome dado a dois matemáticos europeus que viveram entre os séculos XVIII e XIX – o italiano Paolo Ruffini (1.765 a 1.822) e o inglês William Horner (1786 – 1837), este método foi descrito pela primeira vez, ao que se sabe, no século XI pelo matemático chinês Jia Xian (~1.010 a ~1.070) em seu manuscrito Shi Suo Suan Shu (A chave para a matemática), obra esta que se perdeu. A primeira coisa a se fazer para utilizar este método é modificar a equação cúbica original, deixando-a como abaixo:
$$ f\left ( x \right )=x^{3}+2x^{2}+10x-20 $$
Em seguida, adotamos diferentes valores para x no intuito de zerar, ou encontrar a raiz, de f(x). Definindo para x o valor zero, temos:
$$ f\left ( 0 \right )=0^{3}+2.0^{2}+10.0-20 $$
$$ f\left ( 0 \right )=-20 $$
Como f(x) está longe de ser zero, escolhemos um novo valor para x, por exemplo, 1. Como resultado, temos:
$$ f\left ( 1 \right )=1^{3}+2.1^{2}+10.1-20 $$
$$ f\left ( 1 \right )=1+2+10-20 $$
$$ f\left ( 1 \right )=-7 $$
Ainda não foi desta vez que f(x) zerou, pois continua negativo. Então, adotando para x o valor 2, vem:
$$ f\left ( 2 \right )=2^{3}+2.2^{2}+10.2-20 $$
$$ f\left ( 2 \right )=8+8+20-20=36-20 $$
$$ f\left ( 2 \right )=16 $$
Observa-se que, além de f(x) não ter zerado, ele agora é positivo. Então o valor correto para x encontra-se entre 1 e 2, ou seja:
$$ 1< x< 2 $$
Com essa informação em mãos, podemos iniciar a aplicação do método Ruffini-Horner. Monte o esquema abaixo, posicionando à direita as constantes da equação cúbica:
$$ f\left ( x \right )=x^{3}+2x^{2}+10x-20 $$

Em seguida, à esquerda, colocamos a primeira estimativa para o valor da nossa raiz. Como a raiz é maior que 1 e menor que 2, então ela vale 1 vírgula alguma coisa. Nossa primeira estimativa, portanto, será 1:

Agora, aplica-se o algoritmo que caracteriza o método: multiplica-se o valor estimado da raiz (1) pela primeira constante (1), somado ao valor abaixo da primeira constante (que não há). O resultado é 1, que posicionamos abaixo da segunda constante (2):

Repete-se o algoritmo: multiplica-se a raiz (1) pela segunda constante (2), cujo resultado (2) é somado ao valor abaixo da segunda constante (1). O resultado é 3, que posicionamos abaixo da terceira constante (10):

Mais uma vez: multiplica-se a raiz (1) pela terceira constante (10), cujo resultado (10) é somado ao valor abaixo da terceira constante (3). O resultado é 13, que posicionamos abaixo da quarta constante (-20):

Feito isso, agora somamos os resultados parciais das colunas à direita, conforme abaixo:

Repete-se o procedimento anterior para a linha das somas parciais (números vermelhos), exceto para a última coluna à direita (-7 em cinza), que compõe o primeiro resultado da rodada. Executando o algoritmo, multiplica-se a raiz (1) pela primeira constante vermelha (1), cujo resultado (1) é somado ao valor abaixo da primeira constante vermelha (que não há). O resultado é 1, que posicionamos abaixo da segunda constante vermelha (3):

Mais uma vez: multiplica-se a raiz (1) pela segunda constante vermelha (3), cujo resultado (3) é somado ao valor abaixo da segunda constante vermelha (1). O resultado é 4, que posicionamos abaixo da terceira constante (13):

Agora, somam-se os resultados parciais das colunas à direita, conforme abaixo:

Repete-se o procedimento anterior para a nova linha de somas parciais (números azuis), exceto para a última coluna à direita (17 em cinza), que compõe o segundo resultado da rodada. Executando o algoritmo, multiplica-se a raiz (1) pela primeira constante azul (1), cujo resultado (1) é somado ao valor abaixo da primeira constante azul (que não há). O resultado é 1, que posicionamos abaixo da segunda constante azul (4):

Como não há mais números a serem multiplicados (pois o próximo já está destacado em cinza), resta-nos somar os resultados parciais das colunas à direita, conforme abaixo:

Esta rodada está completa, e os números em cinza formam a nova equação cúbica após a aplicação do algoritmo:
$$ f\left ( x \right )=x^{3}+5x^{2}+17x-7 $$
O próximo passo consiste em dilatar esse polinômio, multiplicando cada termo por um fator de dez, conforme abaixo:
$$ f\left ( x \right )=x^{3}\times \left ( 10^{0} \right )+5x^{2}\times \left ( 10^{1} \right )+17x\times \left ( 10^{2} \right )-7\times \left ( 10^{3} \right ) $$
$$ f\left ( x \right )=x^{3}\times 1+5x^{2}\times 10+17x\times 100-7\times 1000 $$
$$ f\left ( x \right )=x^{3}+50x^{2}+1700x-7000 $$
Com o polinômio dilatado, estimamos mais uma vez o valor de x de modo a zerar f(x). Fazendo x = 2, temos:
$$ f\left ( 2 \right )=2^{3}+50\times 2^{2}+1700\times 2-7000 $$
$$ f\left ( 2 \right )=8+200+3400-7000 $$
$$ f\left ( 2 \right )=-3392 $$
Como f(x) resultou negativo, aumentamos o valor de x para 3, resultando:
$$ f\left ( 3 \right )=3^{3}+50\times 3^{2}+1700\times 3-7000 $$
$$ f\left ( 3 \right )=27+450+5100-7000 $$
$$ f\left ( 3 \right )=-1423 $$
Como f(x) ainda é negativo, aumentamos o valor de x para 4, obtendo:
$$ f\left ( 4 \right )=4^{3}+50\times 4^{2}+1700\times 4-7000 $$
$$ f\left ( 4 \right )=64+800+6800-7000 $$
$$ f\left ( 4 \right )=664 $$
Como agora f(x) é positivo, então o número que compõe a raiz fica entre 3 e 4, ou seja:
$$ 3< x< 4 $$
O valor de x é 3 vírgula alguma coisa. Então nossa nova estimativa é 3. Aplicando o algoritmo como descrito nos passos anteriores, o resultado já consolidado será:

Esta rodada está completa, e os números em cinza formam a nova equação cúbica após a aplicação do algoritmo:
$$ f\left ( x \right )=x^{3}+59x^{2}+2015x-1747 $$
Ao dilatarmos esse polinômio, multiplicando cada termo por um fator de dez, temos:
$$ f\left ( x \right )=x^{3}\times \left ( 10^{0} \right )+59x^{2}\times \left ( 10^{1} \right )+2015x\times \left ( 10^{2} \right )-1747\times \left ( 10^{3} \right ) $$
$$ f\left ( x \right )=x^{3}+590x^{2}+201.500x-1.747.000 $$
A nova estimativa para x na tentativa de zerar o f(x), seguindo o procedimento anterior, será 6 vírgula alguma coisa. Então nossa nova estimativa é 6. Aplicando o algoritmo como descrito nos passos anteriores o resultado, já consolidado, será:

E assim sucessivamente vamos gerando o número irracional procurado. A raiz obtida até aqui é:
$$ \mu \cong 1,36... $$
Condizente com o resultado fornecido por Fibonacci. Havia, porém, um segundo método que ele poderia ter utilizado para resolver a equação cúbica, apresentado no capítulo 13 do Liber Abaci, intitulado Aqui começa o capítulo treze sobre o método Elchataym e como com ele quase todos os problemas de matemática são resolvidos. Leonardo explica que o método árabe al-khata’ayn (literalmente: “os dois erros”) pode ser traduzido como o método da posição falsa dupla, e que hoje conhecemos como interpolação linear. No início do capítulo 14 do Liber Abaci, Fibonacci usa uma modificação desta técnica para aproximar raízes cúbicas; portanto, esta técnica poderia ter sido utilizada para encontrar a resposta do terceiro problema proposto por João de Palermo. Esta técnica é semelhante àquela apresentada no capítulo Os números irracionais, no terceiro volume desta série. Para aplicar o método elchataym, adotamos o procedimento inicial apresentado no método Ruffini-Horner, em que estimamos o valor de x, de modo a zerar o valor de f(x). Nessa abordagem, para x igual a 1, f(x) vale -7; e para x igual a 2, f(x) vale 16. Para que f(x) seja igual a zero, x deve estar entre 1 e 2. Colocando em um gráfico (sem escala), temos:

Ligando os pares ordenados (x, f(x)) obtidos com as estimativas iniciais através de uma reta (vermelha, acima) interpolamos linearmente o eixo x de modo que o ponto em que este eixo é cortado corresponderá, aproximadamente, à raiz da equação cúbica. Deste modo, por semelhança de triângulos (respectivamente verde e azul), temos a seguinte proporção:
$$ \frac{16-\left ( -7 \right )}{2-1}=\frac{-7-0}{1-x} $$
Resolvendo, obtém-se:
$$ \frac{16+7}{1}=\frac{-7}{1-x} $$
$$ \frac{23}{1}=\frac{-7}{1-x} $$
$$ 23\left ( 1-x \right )=-7 $$
$$ 23-23x=-7 $$
$$ 23+7=23x $$
$$ x=\frac{30}{23}\cong 1,30434782... $$
A reta corta o eixo x no ponto 30/23. Apesar de aproximada, esta fração, ou número racional, não representa adequadamente a raiz da equação cúbica, pois a raiz é um número irracional. Assim, se substituirmos, na equação cúbica, o valor de x pelo valor decimal (aproximado) de 30/23, obteremos:
$$ f\left ( 1,3 \right )=\left ( 1,3 \right )^{3}+2\times \left ( 1,3 \right )^{2}+10\times \left ( 1,3 \right )-20 $$
$$ f\left ( 1,3 \right )=2,197+3,38+13-20 $$
$$ f\left ( 1,3 \right )=18,577-20 $$
$$ f\left ( 1,3 \right )=-1,423 $$
Nota-se que f(30/23) gera um racional negativo, ou seja, a interpolação está subestimada. Como o número irracional procurado está entre 1 e 2, outra estimativa válida seria calcular a média entre estes dois números, ou seja:
$$ x=\frac{1+2}{2}=\frac{3}{2}=1,5 $$
Substituindo, na equação cúbica, o valor de x pelo valor decimal de 3/2, obtém-se:
$$ f\left ( 1,5 \right )=\left ( 1,5 \right )^{3}+2\times \left ( 1,5 \right )^{2}+10\times \left ( 1,5 \right )-20 $$
$$ f\left ( 1,5 \right )=3,375+4,5+15-20 $$
$$ f\left ( 1,5 \right )=22,875-20 $$
$$ f\left ( 1,5 \right )=2,875 $$
Observe: f(3/2) agora gera um racional positivo, ou seja, a média entre 1 e 2 gera um resultado superestimado. Se dispuséssemos estas frações em uma régua, a razão 30/23 seria posicionada proporcionalmente entre o número 1 e a fração 3/2:

Se 30/23 é menor que o número procurado e 3/2 é maior, então este número irracional encontra-se entre estes limites fracionários. Obtendo-se a média entre estas razões:

$$ x=\frac{\frac{30}{23}+\frac{3}{2}}{2}=\frac{\frac{60+69}{46}}{2}=\frac{129}{92}\cong 1,40217391... $$
Numa régua, a razão 129/92 será posicionada bem no meio entre as frações 30/23 e 3/2:

Substituindo, na equação cúbica, o valor de x pelo resultado decimal (aproximado) da fração 129/92, obtém-se:
$$ f\left ( 1,4 \right )=\left ( 1,4 \right )^{3}+2\times \left ( 1,4 \right )^{2}+10\times \left ( 1,4 \right )-20 $$
$$ f\left ( 1,4 \right )=2,744+3,92+14-20 $$
$$ f\left ( 1,4 \right )=20,664-20 $$
$$ f\left ( 1,4 \right )=0,664 $$
Observa-se que a fração 129/92 é maior que o número irracional procurado, pois a equação cúbica resultou positiva. Se 30/23 é menor que o número procurado e 129/92 é maior, então este número irracional encontra-se entre estes dois novos limites. Obtendo-se a média entre estas frações:
$$ x=\frac{\frac{30}{23}+\frac{129}{92}}{2}=\frac{\frac{120+129}{92}}{2}=\frac{249}{89}\cong 1,35326086... $$
Numa régua, a razão 249/184 será posicionada bem no meio entre as frações 30/23 e 129/92:

Substituindo, na equação cúbica, o valor de x pelo resultado decimal (aproximado) da fração 249/184, obtém-se:
$$ f\left ( 1,35 \right )=\left ( 1,35 \right )^{3}+2\times \left ( 1,35 \right )^{2}+10\times \left ( 1,35 \right )-20 $$
$$ f\left ( 1,35 \right )=2,460375+3,645+13,5-20 $$
$$ f\left ( 1,4 \right )=19,605375-20 $$
$$ f\left ( 1,4 \right )=-0,394625 $$
Observa-se que a fração 249/184 agora é menor que o número irracional procurado, pois a equação cúbica resultou menor que zero. Seguindo este procedimento de médias e cálculos da equação cúbica com as frações resultantes, aproximamo-nos, a cada rodada, do número irracional procurado. As frações obtidas nas próximas nove sequências, seguindo este método, são:
$$ \frac{507}{368}\cong 1,37771739... $$
$$ \frac{1.005}{736}\cong 1,36548913... $$
$$ \frac{2.019}{1.472}\cong 1,37160326... $$
$$ \frac{4.029}{2.944}\cong 1,36854619... $$
$$ \frac{8.067}{5.888}\cong 1,37007472... $$
$$ \frac{16.125}{11.776}\cong 1,36931046... $$
$$ \frac{32.241}{23.552}\cong 1,36892832... $$
$$ \frac{64.473}{47.104}\cong 1,36873726... $$
$$ \frac{128.995}{94.208}\cong 1,36883279... $$
Com mais algumas iterações, é possível alcançar a mesma precisão de nove casas decimais obtida por Fibonacci e até mais. Entretanto, a resposta ao problema está incorreta na última representação fracionária dada pelo matemático, cujo original é:
$$ 1;22,07,42,33,04,40 $$
Esta representação sexagesimal da raiz cúbica é um fato curioso, uma vez que toda a matemática apresentada em Liber Abaci está desenvolvida em base decimal. De todo modo, a expansão correta da raiz cúbica real tem continuidade com os termos a seguir:
$$ 1;22,07,42,33,04,38,30,50 $$

É possível que Fibonacci tenha cometido esse erro deliberadamente, pelo mesmo motivo que ocultou o seu método de solução: para que ninguém mais pudesse duplicar os seus resultados. Na época de Leonardo, os métodos de um estudioso eram valiosas moedas de troca para obter posições remuneradas com a nobreza, a realeza ou a igreja. Como tal, os estudiosos mantinham seus métodos em segredo de rivais e concorrentes. A audiência de Fibonacci com o imperador Frederico II foi uma excelente oportunidade para mostrar suas habilidades sem revelar seus métodos; para ele, o matemático João de Palermo representaria uma real ameaça ao segredo dos cálculos de que fazia uso, tendo sido uma razão mais que suficiente para que escondesse seus métodos, ao cobrir suas pegadas com um erro premeditado em sua resposta. Por fim, sabe-se que Fibonacci estudara os textos de Khayyam, de quem João de Palermo tomara emprestado o polinômio cúbico de seu terceiro enigma. As equações cúbicas voltariam a ser abordadas, porém sem uma solução geral, por algebristas italianos da região de Florença: em 1.463, Benedetto de Florença, ou Maestro Benedetto, conclui seu trabalho intitulado Trattato di praticha d'arismetica, um volume de 500 páginas dos quais os capítulos 13, 14 e 15 tratam especificamente de equações algébricas, começando com a reghola de algebra amuchable, que trata da solução de seis tipos de equações lineares e quadráticas, cujo texto é considerado uma tradução literal para o italiano de uma tradução latina da álgebra de al-Khwarizmi, seguido das bem conhecidas nomenclaturas para as potências de uma incógnita, tais como segue:

$$ \left\{\begin{matrix}x^{2}=censo=c\\ x^{3}=cubo=b\\ x^{4}=censo\,\, di\,\, censo=cc\end{matrix}\right. $$

O livro 14 deste tratado apresenta uma sequência de 140 problemas numéricos derivados de um manuscrito perdido denominado Trattato di Praticha, escrito pelo mestre florentino Biaggio, falecido por volta de 1.340. Vinte e oito destes problemas são mercantis. Os demais são teóricos, todos conduzindo a equações algébricas pertencentes a tipos solucionados por Benedetto no livro 13. Um destes problemas conduz à equação:

$$ \frac{1}{12}x^{2}+\left ( 2+\frac{1}{12} \right )x+12=x $$

Que, de acordo com Benedetto e Biaggio, non può essere (não pode ser) pois, de fato, essa equação não possui raízes reais. Já no livro 15 deste tratado, Maestro Benedetto inclui uma pequena biografia sobre Maestro Antonio Mazzinghi, que possuía um ateliê em Santa Trinità em Florença e que se tornou famoso não apenas com aritmética e geometria, como também com astrologia e música, tendo falecido por volta de 1.390. Deste outro algebrista, Benedetto cita vários problemas mais complexos, tal como este:

Encontrar três números em proporção contínua tais que sua soma seja igual a 19 e a soma de seus quadrados seja igual a 40.

Em notação moderna, teríamos:

$$ \left\{\begin{matrix}x+y+z=19\\ \frac{x}{y}=\frac{y}{z}\\ x^{2}+y^{2}+z^{2}=40\end{matrix}\right. $$

Porém, em nenhum destes trabalhos encontra-se uma solução geral para as equações cúbicas, de modo que na primeira obra publicada pelo frade e matemático italiano Luca Pacioli em 1.494 (o influente Summa de arithmetica...) ele conclui que para equações cúbicas e quárticas não foi possível até agora formar regras gerais, chegando a afirmar que a resolução das cúbicas era tão impossível quanto a quadratura do círculo! Interessante observar que a postura adotada pelos matemáticos medievais e renascentistas de guardar segredo de seus métodos de cálculo serviu de estopim para descobrir-se enfim a fórmula geral para encontrar as raízes de equações cúbicas e descortina uma história, no mínimo, rocambolesca, que começa por um lado com o matemático italiano Nicolau Fontana Tartaglia (1.499 /1.500 a 1.557).

O matemático italiano Nicolau Fontana Tartaglia.

Além de matemático, foi engenheiro (projetava fortificações), topógrafo (estudava o relevo na busca dos melhores pontos de defesa ou ataque), e um guarda-livros da então República de Veneza. Publicou muitos livros, entre os quais a primeira tradução para o italiano das obras de Arquimedes e de Euclides bem como uma aclamada compilação de matemática. Tartaglia também foi o primeiro a aplicar matemática na investigação da trajetória de projéteis, ou balística, em sua obra Nova Scientia (Nova Ciência); tempos depois, esse trabalho foi parcialmente validado e parcialmente superado pelos estudos de Galileu sobre as quedas de corpos livres.

Trajetória de uma bala de canhão, segundo a concepção de Tartaglia em seu Nova Scientia. Observa-se claramente pela ilustração que a trajetória da bala não é parabólica, um dos aspectos incorretos e posteriormente superados pelos estudos de Galileu Galilei.

Nicolau também chegou a publicar um tratado sobre a recuperação de navios afundados e ainda desenvolveu uma fórmula para calcular o volume de tetraedros (inclusive irregulares), conhecida por fórmula de Tartaglia. Nascido em Brescia e filho de Michele Fontana, um despachante que trabalhava na entrega de correspondências em cidades vizinhas, levava uma existência humilde, porém honesta, com seus pais e suas duas irmãs, tendo começado a frequentar a escola aos quatro anos de idade. A vida poderia ter sido muito diferente para Nicolau não fosse uma tragédia envolvendo sua família quando, em 1.506, então com seis anos de idade, Nicolau viu-se, junto com sua mãe e irmãs, entregues à pobreza após o assassinato de seu pai por assaltantes. Outra tragédia em 1.512 veio somar-se à anterior quando o rei francês Luis XII invadiu Brescia com suas tropas durante a guerra da Liga de Cambrai contra Veneza. As forças militares de Brescia defenderam a cidade por sete dias, sendo enfim derrotadas pelas tropas de Luis XII que, por vingança, mataram mais de 45.000 habitantes de Brescia ao final da batalha. Nicolau, então com doze anos, e sua família refugiaram-se no santuário da catedral da cidade durante a matança, mas o menino foi encontrado por um soldado francês, que com uma espada cortou sua mandíbula e seu pálato, sendo deixado para morrer. Sua mãe, sem dinheiro para pagar um médico, conseguiu salvar o filho lambendo-lhe as feridas; apesar dos desvelos de sua mãe, Nicolau nunca mais recuperaria sua fala normal e, já adulto, usava uma espessa barba para cobrir as fundas cicatrizes que carregava no rosto. Por conta das dificuldades na fala, Nicolau ganhou o apelido de Tartaglia, que significa “gago”. Há uma história que conta que sua mãe, com muito sacrifício, conseguiu juntar dinheiro suficiente para lhe pagar um tutor; os recursos – escassos – acabaram e com eles as aulas, quando Nicolau estava ainda na metade do alfabeto, valendo-se de seu próprio esforço para aprender o restante das letras e alfabetizar-se sozinho. Como auto-didata, possuía uma capacidade extraordinária para a matemática. Entretanto, todas as suas tentativas para aprender o latim fracassaram, motivo que o levou a escrever seus livros apenas em italiano, o que não era muito bem visto naquela época: ser erudito exigia o latim como pré-requisito. Fato é que ele e seus contemporâneos, trabalhando fora das universidades e academias, foram os grandes responsáveis pela difusão das obras clássicas em línguas modernas entre a então emergente classe burguesa letrada. O primeiro contato de Tartaglia com as equações cúbicas deu-se em 1.530, contando então com apenas 24 anos, mas um já respeitado matemático, quando um tal Zuanne de Tonini da Coi – um professor de matemática em Brescia de pouca relevância – mais por ousadia que por prudência, propôs a Tartaglia que solucionasse as duas equações cúbicas abaixo:

$$ \left\{\begin{matrix}x^{3}+3x^{2}=5\\ x^{3}+6x^{2}+8x=1000\end{matrix}\right. $$

Este evento é narrado por Tartaglia em sua obra Quesiti, notadamente no quesito XIV, nestes termos:

QUESITO XIV, proposto a mim em Verona por um Mestre Zuanne de Tonini da Coi, que possui uma escola em Brescia, e trazido a mim por Messer Antonio da Cellatico no ano de 1.530.

Mestre Zuanne – Encontre um número que multiplicado por sua raiz, incrementado de três, seja igual a cinco. De modo análogo, encontre três números tais que o segundo seja maior por dois que o primeiro e o terceiro seja maior por dois que o segundo e onde o produto dos três seja mil.

Nicolau – M. Zuanne: enviaste-me estas suas duas questões como algo impossível de resolver ou, ao menos, como não conhecidas por mim; porém, desenvolvendo-as pela álgebra, a primeira leva à equação de um cubo e 3 censos igual a 5, e a segunda conduz a um cubo e 6 censos e 8 coisas igual a 1.000. De acordo com Fra Luca e outros estas equações tem sido, até agora, consideradas de solução impossível por meio de uma regra geral. Acreditas que com tais questões, possas te colocar acima de mim, tentando aparentar-se um grande matemático. Ouvi dizer que fazes isto com todos os professores desta ciência em Brescia para que eles, por medo dessas perguntas, não se atrevam a conversar contigo; e talvez eles conheçam mais desta ciência que tu mesmo.

Mestre Zuanne – Entendo tanto quanto o que me escrevestes, e que consideras que tais casos são impossíveis.

Nicolau – Eu não disse que tais casos são impossíveis. De fato, para o primeiro caso, em que o cubo e o censo igualam-se a um número, estou convencido de ter encontrado a regra geral, mas no momento quero mantê-la em segredo por diversas razões. Para o segundo caso, em que o cubo e o censo e a coisa igualam-se a um número, confesso não ter sido capaz até o momento de encontrar uma regra geral. Entretanto, estou disposto a apostar contigo 10 ducados contra 5 de que não és capaz de resolver por uma regra geral as duas questões que me propusestes. E isto é algo pelo qual deverias corar, ao propor para outros aquilo que tu mesmo não compreendes, mas finges compreender, buscando alcançar a reputação de ser alguém grande.

O segundo capítulo desta curiosa história descerra-se com o matemático italiano Scipione Del Ferro (1.465 a 1.526). Nascido em Bolonha e professor de matemática na universidade desta mesma cidade, credita-se a ele a primazia pela descoberta de um método de solução de equações cúbicas reduzidas. Nos tempos de Del Ferro, sabia-se que a equação cúbica geral podia ser simplificada para um dos dois casos denominados equações cúbicas reduzidas, para quaisquer números positivos p, q e x. Por exemplo, considere a equação cúbica geral abaixo:
$$ ax^{3}+bx^{2}+cx+d=0 $$
Onde a, b, c e d são reais e a é diferente de zero. Fazendo:
$$ x=y+z $$
Com z a ser determinado, substituindo na cúbica geral, vem:
$$ a\left ( y+z \right )^{3}+b\left ( y+z \right )^{2}+c\left ( y+z \right )+d=0 $$
Expandindo o polinômio:
$$ a\left ( y^{3}+3y^{2}z+3yz^{2}+z^{3} \right )+b\left ( y^{2}2yz+z^{2} \right )+c\left ( y+z \right )+d=0 $$
$$ \left ( ay^{3}+3ay^{2}z+3ayz^{2}+az^{3} \right )+\left ( by^{2}2byz+bz^{2} \right )+\left ( cy+cz \right )+d=0 $$
Agrupando os termos comuns:
$$ ay^{3}+\left ( 3az+b \right )y^{2}+\left ( 3az^{2}+2bz+c \right )y+\left ( az^{3}+bz^2+cz+d \right )=0 $$
Impondo que:
$$ 3az+b=0 $$
Isolando z desta equação resulta:
$$ z=-\frac{b}{3a} $$
O primeiro par de parênteses do polinômio expandido (que está sendo multiplicado por y²) é nulo. A substituição do valor de z no segundo par de parênteses da equação com os termos comuns agrupados fornece:
$$ \left ( 3az^{2}+2bz+c \right ) $$
$$ \left ( 3a\left ( \frac{-b}{3a} \right )^{2}+2b\left ( \frac{-b}{3a} \right )+c \right ) $$
$$ \left ( 3a\frac{b^{2}}{9a^{2}}-\frac{2b^{2}}{3a}+c \right ) $$
$$ \left ( \frac{b^{2}}{3a}-\frac{2b^{2}}{3a}+c \right ) $$
$$ \left ( -\frac{b^{2}}{3a}+c \right ) $$
E a substituição do valor de z no terceiro par de parênteses da equação com os termos comuns agrupados fornece:
$$ \left ( az^{3}+bz^{2}+cz+d \right ) $$
$$ \left ( a\left ( \frac{-b}{3a} \right )^{3}+b\left ( \frac{-b}{3a} \right )^{2}+c\left ( \frac{-b}{3a} \right )+d \right ) $$
$$ \left ( \left ( \frac{-b^{3}}{27a^{2}} \right )+\left ( \frac{b^{3}}{9a^{2}} \right )+c\left ( \frac{-b}{3a} \right )+d \right ) $$
$$ \left ( \left ( \frac{-b^{3}+3b^{3}}{27a^{2}} \right )+c\left ( \frac{-b}{3a} \right )+d \right ) $$
$$ \left ( \frac{2b^{3}}{27a^{2}}-\frac{cb}{3a}+d \right ) $$
Assim, a equação cúbica:
$$ ay^{3}+\left ( 3az+b \right )y^{2}+\left ( 3az^{2}+2bz+c \right )y+\left ( az^{3}+bz^2+cz+d \right )=0 $$
Fica modificada conforme abaixo:
$$ ay^{3}+\left ( -\frac{b^{2}}{3a}+c \right )y+\left ( \frac{2b^{3}}{27a^{2}}-\frac{cb}{3a}+d \right )=0 $$
Por fim, multiplicando toda a equação por 1/a resulta:
$$ \frac{1}{a}\left [ ay^{3}+\left ( -\frac{b^{2}}{3a}+c \right )y+\left ( \frac{2b^{3}}{27a^{2}}-\frac{cb}{3a}+d \right ) \right ]=0 $$
$$ a\frac{1}{a}y^{3}+\frac{1}{a}\left ( -\frac{b^{2}}{3a}+c \right )y+\frac{1}{a}\left ( \frac{2b^{3}}{27a^{2}}-\frac{cb}{3a}+d \right )=0 $$
$$ y^{3}+\left ( -\frac{b^{2}}{3a^{2}}+\frac{1}{ca} \right )y+\left ( \frac{2b^{3}}{27a^{3}}-\frac{cb}{3a^{2}}+\frac{d}{a} \right )=0 $$
Renomeando o segundo termo para:
$$ \left ( -\frac{b^{2}}{3a^{2}}+\frac{1}{ca} \right )=p $$
E renomeando o terceiro termo para:
$$ \left ( \frac{2b^{3}}{27a^{3}}-\frac{cb}{3a^{2}}+\frac{d}{a} \right )=q $$
A equação cúbica geral fica reduzida a:
$$ y^{3}+py+q=0 $$
O que os matemáticos daquela época consideravam como os dois casos para equações cúbicas reduzidas seriam:
$$ \left\{\begin{matrix}y^{3}+py=q\\ y^{3}=py+q\end{matrix}\right. $$
Como os valores de a, b, c e d são conhecidos e como:
$$ \left\{\begin{matrix}x=y+z\\ z=-\frac{b}{3a}\end{matrix}\right. $$
Encontrando-se o valor de y facilmente chega-se ao valor de x, que é a raiz da equação cúbica original. Entretanto, nenhum manuscrito de Del Ferro sobreviveu, em grande parte devido à sua resistência em comunicar os resultados de seus trabalhos, prática comum naquela época. Ao invés de publicar suas idéias, ele as teria mostrado somente a um pequeno e seleto grupo de amigos e estudantes. Como visto no desafio de João de Palermo contra Fibonacci, era costume entre os matemáticos desafiarem-se uns aos outros. Quando um matemático aceitava o desafio de outro, geralmente cada matemático tinha que solucionar um conjunto de problemas propostos pelo seu oponente, dentro de um prazo fixado, numa quantidade previamente acordada e cujo conteúdo era mantido em segredo até a data da troca das listas contendo os problemas. Curiosamente, esses eventos atraíam grandes multidões, entre estudiosos das universidades, partidários dos desafiantes, membros da nobreza, da burguesia e a população em geral. Muitas vezes o perdedor era abandonado por seu patrono (que o financiava) ou era obrigado a deixar a posição que ocupava na universidade em que lecionasse. Ao vencedor desses confrontos a recompensa se traduzia essencialmente em estabilidade no emprego, novas ofertas de trabalho e até um reforço no aporte monetário oferecido por seu patrono, a quem era prestada assessoria matemática para assuntos, em geral, financeiros. É possível que Del Ferro temesse ser desafiado, daí porque mantivesse seu maior segredo profissional a salvo da concorrência, para que pudesse ser utilizado nessas situações. Especula-se que Scipione tenha trabalhado na busca dessa solução como consequência da breve passagem do prestigiado Luca Pacioli pela Universidade de Bolonha, entre 1.501 e 1.502, para proferir algumas palestras. Acredita-se que Pacioli tenha incentivado Del Ferro a tentar resolver esse problema, dada sua manifesta destreza em manipulações algébricas com radicais. Posteriormente, em 1.509, Pacioli publicaria sua tradução para o italiano do Elementos de Euclides, que acabou por se tornar uma fonte de conhecimento matemático para os seus conterrâneos não versados em latim. Os estudiosos italianos, dando continuidade ao trabalho desenvolvido por Euclides em seu livro X, aprofundaram-se no estudo das somas e diferenças de raízes quadradas, tais como:
$$ \left\{\begin{matrix}a+\sqrt{b}\\ \sqrt{a}+\sqrt{b}\\ \sqrt{a}-\sqrt{b}\end{matrix}\right. $$
Estas somas eram denominadas binomiais (binomiums em latim) e as diferenças, restos (no latim, apotemes).

O frade franciscano Luca Bartolomeo de Pacioli, com um estudante à sua direita (talvez Guidobaldo da Montefeltro). Pintura atribuída a Jacopo de Barbari, de 1.495. Observe um sólido platônico no canto inferior direito da tela.

Ao longo dessas pesquisas, os estudiosos perceberam que a diferença de raízes quadradas representada por:
$$ x=\sqrt{a+\sqrt{b}}-\sqrt{a-\sqrt{b}} $$
Ao ser elevada ao quadrado:
$$ x^{2}=\left ( \sqrt{a+\sqrt{b}}-\sqrt{a-\sqrt{b}} \right )^{2} $$
E desenvolvido o lado direito da igualdade:
$$ \left ( \sqrt{a+\sqrt{b}}-\sqrt{a-\sqrt{b}} \right )\times \left ( \sqrt{a+\sqrt{b}}-\sqrt{a-\sqrt{b}} \right ) $$
$$ \left ( \sqrt{a+\sqrt{b}} \right )^{2}-\sqrt{\left ( a+\sqrt{b} \right )\left ( a-\sqrt{b} \right )}-\sqrt{\left ( a-\sqrt{b} \right )\left ( a+\sqrt{b} \right )}+\left ( \sqrt{a-\sqrt{b}} \right )^{2} $$
$$ a+\sqrt{b}-\sqrt{a^{2}-a\sqrt{b}+a\sqrt{b}-\left ( \sqrt{b} \right )^{2}}-\sqrt{a^{2}+a\sqrt{b}-a\sqrt{b}-\left ( \sqrt{b} \right )^{2}}+a-\sqrt{b} $$
$$ 2a-\sqrt{a^{2}-b}-\sqrt{a^{2}-b} $$
Resultava em:
$$ x^{2}=2a-2\sqrt{a^{2}-b} $$
Ou seja, obtemos uma equação quadrática que perdeu o termo linear x. Não se sabe qual a abordagem utilizada por Del Ferro para gerar a sua fórmula, porém, do mesmo modo que os estudiosos faziam uso da soma e diferença de raízes quadradas para produzir equações quadráticas reduzidas (sem o termo x), procedimento similar teria sido utilizado por Del Ferro, somando e subtraindo raízes cúbicas para se chegar a uma equação cúbica reduzida (sem o termo quadrático: x²). Supondo que sua linha de raciocínio tenha seguido algo como a diferença entre raízes cúbicas, conforme abaixo:
$$ x=\sqrt[3]{a+\sqrt{b}}-\sqrt[3]{a-\sqrt{b}} $$
Fazendo-se, por simplificação, as seguintes substituições:
$$ \left\{\begin{matrix}\alpha =\sqrt[3]{a+\sqrt{b}}\\ \beta =\sqrt[3]{a-\sqrt{b}}\end{matrix}\right. $$
Resulta:
$$ x=\alpha -\beta $$
Elevando ao cubo:
$$ x^{3}=\left ( \alpha -\beta \right )^{3} $$
Expandindo o binômio:
$$ x^{3}=\left ( \alpha -\beta \right )\times \left ( \alpha -\beta \right )\times \left ( \alpha -\beta \right ) $$
$$ x^{3}=\left ( \alpha ^{2}-2\alpha \beta +\beta ^{2} \right )\times \left ( \alpha -\beta \right ) $$
$$ x^{3}=\alpha ^{3}-3\alpha ^{2}\beta +3\alpha \beta ^{2}-\beta ^{3} $$
Colocando 3αβ em evidência:
$$ x^{3}=\alpha ^{3}-3\alpha \beta \left ( \alpha -\beta \right )-\beta ^{3} $$
Mas x = (α – β), o que nos conduz à cúbica reduzida:
$$ x^{3}=\alpha ^{3}-\beta ^{3}-3\alpha \beta x $$
Restituindo a α e a β seus valores originais, temos:
$$ x^{3}=\left ( \sqrt[3]{a+\sqrt{b}} \right )^{3}-\left ( \sqrt[3]{a-\sqrt{b}} \right )^{3}-3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right )x $$
Desenvolvendo o lado direito desta igualdade:
$$ x^{3}=a+\sqrt{b}-a+\sqrt{b}-3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right )x $$
$$ x^{3}=2\sqrt{b}-3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right )x $$
Rearranjando os termos:
$$ x^{3}+3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right )x=2\sqrt{b} $$
O que equivale a:
$$ x^{3}+px=q $$
Onde:
$$ p=3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right ) $$
E:
$$ q=2\sqrt{b} $$
Isolando a constante b da equação acima, temos:
$$ \frac{q}{2}=\sqrt{b} $$
$$ \left (\frac{q}{2} \right )^{2}=\left (\sqrt{b} \right )^{2} $$
$$ \left (\frac{q}{2} \right )^{2}=b $$
Seguindo o mesmo procedimento para isolar a constante a, vem:
$$ p=3\left ( \sqrt[3]{a+\sqrt{b}} \right )\left ( \sqrt[3]{a-\sqrt{b}} \right ) $$
$$ \frac{p}{3}=\sqrt[3]{\left (a+\sqrt{b} \right )\times \left (a-\sqrt{b} \right )} $$
$$ \left (\frac{p}{3} \right )^{3}=\left (\sqrt[3]{\left (a+\sqrt{b} \right )\times \left (a-\sqrt{b} \right )} \right )^{3} $$
$$ \left (\frac{p}{3} \right )^{3}=\left (a+\sqrt{b} \right )\times \left (a-\sqrt{b} \right ) $$
$$ \left (\frac{p}{3} \right )^{3}=a^{2}-a\sqrt{b}+a\sqrt{b}-b $$
$$ \left (\frac{p}{3} \right )^{3}=a^{2}-b $$
Como o valor de b já foi estabelecido temos que:
$$ \left (\frac{p}{3} \right )^{3}=a^{2}-\left ( \frac{q}{2} \right )^{2} $$
$$ a^{2}=\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3} $$
$$ a=\sqrt{\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3}} $$
Substituindo a e b na equação original:
$$ x=\sqrt[3]{a+\sqrt{b}}-\sqrt[3]{a-\sqrt{b}} $$
Resulta:
$$ x=\sqrt[3]{\sqrt{\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3}}+\sqrt{\left ( \frac{q}{2} \right )^{2}}}-\sqrt[3]{\sqrt{\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3}}-\sqrt{\left ( \frac{q}{2} \right )^{2}}} $$
$$ x=\sqrt[3]{\sqrt{\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3}}+\left ( \frac{q}{2} \right )}-\sqrt[3]{\sqrt{\left ( \frac{q}{2} \right )^{2}+\left (\frac{p}{3} \right )^{3}}-\left ( \frac{q}{2} \right )} $$
$$ x=\sqrt[3]{\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}-\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} $$
Finalmente, a fórmula tão zelosamente guardada por Del Ferro e descoberta por volta de 1.515, fica:
$$ x=\sqrt[3]{\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} $$
Apesar da diligência de manter em sigilo a fórmula de solução da cúbica reduzida, Scipione possuía um caderno de anotações onde apontava todas as suas descobertas. Após sua morte em 1.526, esse caderno de anotações foi herdado pelo seu genro Aníbal della Nave, casado com a filha de Del Ferro, Filipa. Nave também foi um matemático formado por Scipione e, com a morte do sogro, acabou por substituí-lo na Universidade de Bolonha. Outro aluno de Scipione que teve acesso à solução da equação cúbica reduzida foi Antônio Maria del Fiore, que, ademais, não passava de um matemático irrelevante. Tal como seu mestre, não publicou a fórmula de que detinha a posse, mas resolveu usar este conhecimento secreto em um momento apropriado. De algum modo a notícia de que Tartaglia encontrara uma solução para a provocação de Zuanne da Coi com suas equações cúbicas chegou aos ouvidos de Del Fiore e este, desejoso de obter fama e prestígio entre os matemáticos, e acreditando no potencial de seu segredo, em 1.535 desafia publicamente o consagrado Tartaglia para uma disputa, que prontamente a aceita – acostumado que estava a estes embates matemáticos – principalmente porque nunca ouvira falar de Del Fiore. Os termos do desafio foram estabelecidos: cada um deveria propor a seu oponente uma lista de 30 problemas a serem encaminhados em um envelope, lacrado, a um tabelião. Uma vez de posse do envelope que lhe cabia, a cada desafiante seria dado um prazo de até 50 dias para solucionar sua lista, saindo vencedor aquele que resolvesse corretamente o maior número de problemas. Segundo certos historiadores, ao perdedor caberia pagar a conta de um banquete, a ser oferecido ao vencedor e a mais 30 de seus amigos. Por conta de sua experiência neste tipo de contenda, Tartaglia desconfiava que Del Fiore tivesse algum trunfo poderoso guardado na manga, do contrário não o teria desafiado, suspeita essa confirmada quando Tartaglia obteve a informação de que Del Fiore de fato conhecia um método de resolução para as equações cúbicas. Pressentindo que esta seria a tônica da lista de problemas de seu oponente, Tartaglia mergulhou de cabeça na tentativa de resolução das cúbicas do tipo:
$$ \left\{\begin{matrix}ax^{3}+bx=c\\ ax+b=x^{3}\end{matrix}\right. $$
no que foi plenamente coroado de êxito apenas uma semana antes da retirada dos envelopes; como já soubesse resolver as cúbicas do tipo:
$$ x^{3}+ax^{2}=b $$
aquando do desafio proposto por Zuanne da Coi, Tartaglia finalmente supunha-se bem municiado para enfrentar Del Fiore com segurança. Chega o dia 23 de Fevereiro de 1.535, data do confronto. Contando com uma grande platéia reunida para assistir à disputa, os envelopes são abertos e as suspeitas de Tartaglia ratificadas: a lista de seu oponente continha apenas problemas envolvendo equações cúbicas do tipo solucionado por seu mestre Del Ferro, do tipo:
$$ ax^{3}+bx=c $$
Já a lista de Tartaglia abordava diversos temas matemáticos e, entre as equações cúbicas, todas as formas por ele estudadas e solucionadas, para mostrar que eu tinha pouca consideração por Del Fiore e não tinha motivos para temê-lo, segundo suas próprias palavras. O resultado foi que em pouco mais de duas horas Tartaglia resolveu por completo a lista proposta por Del Fiore! Este, por sua vez, no mesmo intervalo de tempo não conseguiu resolver sequer um único problema da lista que tinha em mãos. Tartaglia completou a humilhação imposta a Del Fiore ao não aceitar deste o custeio do banquete a que tinha direito, desejando nada receber de um tão mau jogador. Depois deste triste episódio, ao pobre Del Fiore restou a obscuridade completa, e até hoje é lembrado apenas por ter pretendido obter fama e fortuna desafiando alguém muito mais competente que ele próprio... O último desdobramento desta história peculiar tem como personagem principal o matemático italiano Girolamo Cardano (1.501 – 1.576), também conhecido por sua alcunha latina Hieronymus Cardanus ou ainda Jérôme Cardan, em francês.

O matemático italiano Gerolamo Cardano.

Cardano foi um polímata (quem estuda ou domina muitas ciências), cujos interesses e proficiências abrangiam áreas tão díspares quanto matemática, medicina, biologia, física, química, astronomia, astrologia, filosofia, literatura e jogos. Atribui-se a ele a invenção parcial e a descrição de diversos dispositivos mecânicos, incluindo: o cadeado de combinação e o eixo cardan com juntas universais.

À esquerda: cadeado de combinação.À direita: o eixo cardan com juntas universais.

Acima: eixo cardan com juntas universais conectado entre o motor e o eixo traseiro do carro.

Filho ilegítimo do advogado Fazio Cardano – que por sua vez era amigo de Leonardo Da Vinci e a quem chegou a prestar auxílio em questões sobre geometria, tal era a sua experiência em matemática – com a jovem viúva Chiara Micheria. Além de sua prática jurídica, Fazio lecionava geometria, tanto na Universidade da Pávia quanto, por um período mais prolongado, na fundação Piatti em Milão. Com cerca de cinquenta anos, Fazio veio a conhecer Chiara Micheria, que era uma jovem viúva na faixa dos trinta, lutando para criar seus três filhos. Deste relacionamento, Chiara fica grávida de Girolamo, mas, antes de dar à luz, a peste bubônica atinge Milão e Chiara é persuadida a deixar a cidade para a segurança relativa da vizinha Pávia, junto aos ricos amigos de Fazio, onde Girolamo viria a nascer. Entretanto, a alegria de sua mãe dura pouco, quando pouco depois recebe a notícia de que seus três primeiros filhos haviam morrido em Milão, atingidos pela peste. Chiara morou afastada de Fazio por longos anos, porém, mais tarde na vida, vieram a se casar. Depois de uma infância deprimente, adoecendo com frequência e enfrentando a áspera educação de seu pai dominador, finalmente em 1.520 Cardano entra para a Universidade de Pávia atraído pela filosofia e ciências, contra o desejo de seu pai, que o queria estudando direito. No entanto, durante a guerra italiana de 1.521-1.526, as autoridades de Pávia foram obrigadas a fechar a universidade em 1.524. Cardano retomou seus estudos na Universidade de Pádua, formando-se em medicina em 1.525. Pouco tempo depois de sua mudança para Pádua seu pai falece, mas nesse interregno estava em plena campanha para o cargo de reitor. Apesar de aluno brilhante, era franco e deveras crítico, chegando ele mesmo a afirmar:

Isto reconheço eu como único e notável entre as minhas falhas: o hábito, no qual persisto, de preferir dizer, acima de tudo, o que sei que desagradará aos ouvidos dos meus ouvintes. Estou ciente disso, contudo mantenho-o deliberadamente, de modo algum ignorante de quantos inimigos faço para mim.

Todavia, sua campanha para reitor foi bem sucedida, superando o seu rival por um único voto. Por outro lado, Cardano desperdiçou a pequena herança que recebeu de seu pai ao transformá-la em apostas para aumentar suas finanças: jogos de cartas, dados e xadrez foram as ferramentas utilizadas para ganhar a vida. O jogo tornou-se-lhe um vício que por anos o consumiu, roubando-lhe valioso tempo, dinheiro e reputação. Sua facilidade em calcular probabilidades nos jogos que disputava (onde mais ganhava que perdia, apesar de tudo) fez com que escrevesse, em 1.526, o Liber de ludo aleae (Livro dos jogos de azar), antecipando-se em quase um século aos trabalhos que viriam a ser desenvolvidos nessa área por Blaise Pascal e Pierre de Fermat. Já formado em medicina, Cardano busca unir-se ao Colégio de Médicos em Milão, onde sua mãe ainda vivia, lançando sua candidatura. O Colégio, porém, recusa-se em admití-lo, apesar do respeito que ganhara como estudante excepcional, dada sua reputação de homem de difícil trato; além disso, a descoberta do nascimento ilegítimo de Cardano ofereceu à junta do Colégio um motivo a mais para rejeitar seu pedido.

Batalha de Pávia, parte das guerras italianas – artista flamengo desconhecido (posterior a 1.525). Esta guerra colocou o rei Francis I da França e a República de Veneza contra o sacro imperador romano Carlos V, o rei Henrique III da Inglaterra e os estados Papais.

Nestas circunstâncias, e a conselho de um amigo, dirige-se a Sacco, uma pequena aldeia a 15 km de Pádua, iniciando uma não muito bem sucedida carreira médica. No final de 1.531 Cardano casa-se com Lucia Bandarini, filha de seu vizinho Aldobello Bandarini, um capitão da milícia local. Antes da morte da esposa, em 1.546, ganham três filhos: Giovanni Battista (1.534), Chiara (1.537) e Aldo (1.543); Cardano posteriormente escreveu que estes foram os anos mais felizes de sua vida. O ofício de médico em Sacco, todavia, não lhe proporcionava renda suficiente para sustentar uma esposa, de modo que, em abril de 1.532, mudam-se para Gallarate, perto de Milão. Novamente candidata-se ao Colégio de Médicos, e novamente tem seu pleito rejeitado. Incapaz de praticar a medicina em Gallarate, Cardano volta a jogar numa tentativa de ganhar dinheiro para pagar suas contas, mas as coisas correm tão mal que se vê forçado a penhorar as jóias de sua esposa e até mesmo parte da mobília. Buscando desesperadamente uma mudança de rumo, os Cardano mudam-se para Milão em 1.533, mas uma vez aqui a situação piora ainda mais, forçando-os a entrar ignominiosamente na pobreza. Mas então a sorte decide enfim sorrir ao desafortunado matemático quando lhe é oferecido o antigo posto de professor de matemática que pertencia a seu pai, Fazio, na fundação Piatti em Milão, dando-lhe tempo livre que foi logo aproveitado para tratar de alguns pacientes, apesar de não ser um membro do Colégio dos Médicos. Quis o destino que Cardano alcançasse algumas curas quase milagrosas e sua crescente reputação como médico o levou a ser consultado às ocultas até mesmo por membros do Colégio dos Médicos. Seus pacientes, curados e agradecidos, bem como seus familiares, tornaram-se seus adeptos fervorosos e, desta forma, Cardano constrói uma base influente de patrocinadores. Apesar do êxito logrado, ele ainda estava furioso com a sua contínua exclusão do Colégio e, em 1.536, publica de forma precipitada um livro atacando não só a habilidade médica, mas o caráter dos membros dessa instituição:

As coisas que mais reputação imprimem a um médico hoje em dia são os seus modos, serviçais, carruagens, roupas, esperteza e perspicácia, todos exibidos de uma maneira artificial e insípida...

Como o leitor poderá imaginar, definitivamente esta não é a melhor maneira de tratar um grupo de pessoas de quem se espera obter um favor; portanto, é óbvio que o novo pedido de Cardano, feito em 1.537 pleiteando uma vez mais o seu ingresso no Colégio de Médicos de Milão, foi uma vez mais rejeitado. No entanto, dois anos depois, após muita pressão de seus admiradores, o Colégio modificou a cláusula relativa a nascimentos legítimos, admitindo Cardano em seu quadro de associados. Ainda nesse mesmo ano (1.539), ele viria a publicar seus dois primeiros livros sobre matemática, sendo que o Pratica Arithmeticæ et mensurandi singularis (Prática da aritmética e medição simples) indica que feitos maiores estavam por vir. Este foi o início da prolífica carreira literária de Cardano em uma diversidade de temas: medicina, filosofia, astronomia e teologia, além de matemática. Foi ainda em 1.536, após os ataques de Girolamo contra a liga médica de Milão que entra em cena o último personagem desta trama: Ludovico Ferrari. Seu avô, Bartolomeu Ferrari, viu-se forçado a deixar o seu lar em Milão para instalar-se em Bolonha devido às guerras italianas – em que não somente as famílias poderosas do norte da Itália lutavam pelo controle das cidades dessa região, expandindo suas áreas de influência pela força, como também a França, o sacro imperador romano e o Papa tentavam abocanhar esses territórios com seus exércitos. Bartolomeu tinha dois filhos: Vicente e Alexandre, este último pai de Ludovico. Inicialmente criado na casa de seu pai, Ludovico passa a viver com seu tio Vicente depois que seu pai foi morto. Vicente tinha um filho, Luca, rapaz difícil, que um belo dia decide sair de casa e procurar emprego; viajando para Milão, descobre que Cardano está à procura de um criado. Conseguindo a vaga, porém, não se adapta ao trabalho e percebe algum tempo depois que sua situação era bem melhor na casa paterna, para onde volta sem dar satisfação alguma ao patrão.

Vista moderna da Galeria Vittorio Emanuele II, tradicional ponto turístico de Milão.

Mas Cardano entra em contato com Vicente Ferrari solicitando que lhe mande de volta o rebento para retomar o emprego como criado. Vicente, entretanto, vê neste retorno do filho rebelde uma oportunidade de mantê-lo por perto, e joga a responsabilidade do emprego nas costas do sobrinho. Assim, em 30 de Novembro de 1.536, contando apenas catorze anos, Ludovico chega à casa de Cardano para substituir o primo como criado da casa. O patrão, depois de descobrir que o menino sabia ler e escrever, escusa-o do serviço de criadagem para torná-lo seu secretário. Em pouco tempo constata que o jovem rapaz tem uma mente excepcional e decide ensinar-lhe matemática. Ferrari recompensou o seu mestre auxiliando-o em seus manuscritos e, quando contava apenas 18 anos, começou a lecionar. Em 1.541 Cardano declina gentilmente de sua posição na fundação Piatti de Milão, recomendando em seu lugar o jovem pupilo, que facilmente derrota em um debate o único rival para o posto, ninguém menos que o nosso já conhecido Zuanne da Coi! Deste modo, contando apenas vinte anos, Ferrari torna-se um conferencista público em geometria pela fundação. Um dos livros em que Ferrari prestou auxílio ao patrão e tutor foi o Pratica Arithmeticæ et mensurandi singularis, de 1.539. Durante a elaboração desta obra, Cardano estudou o Summa de arithmetica e leu os comentários de Luca Pacioli quanto à impossibilidade de solução das cúbicas; também, por muitos anos, tentou descobrir uma fórmula geral que as solucionasse, sem sucesso. Porém, no mesmo ano da publicação desta obra, Cardano tomou conhecimento da vitória retumbante na contenda de Tartaglia sobre Del Fiore envolvendo a resolução de equações cúbicas, ocorrida quatro anos antes, e ensaia uma aproximação com o matemático gago ao enviar o livreiro Zuan Antonio de Bassaro, seu preposto, para solicitar a Tartaglia que fornecesse o seu método de solução, pois que as fórmulas poderiam ser incluídas em um livro que estava para ser publicado em breve. Tartaglia recusou a proposta, informando que publicaria suas fórmulas em um livro de sua própria autoria. Cardano não desiste e escreve muitas e muitas vezes a Tartaglia, implorando para que revele seu segredo e, em todas, seu pedido é recusado. Mudando de estratégia, Cardano convida Tartaglia à sua residência com a promessa de apresentá-lo ao vice-rei e comandante-em-chefe espanhol em Milão, Alfonso D’Avalos, ciente que estava dos recentes progressos de Tartaglia nos estudos de balística com a publicação de seu livro Nova Scientia. Este contato soava tentador, pois poderia fornecer uma boa renda caso o vice-rei contratasse Tartaglia para prestar serviços relacionados à artilharia. O ardil funcionou e após aceitar o convite, em 25 de Março de 1.539 Tartaglia chega em Milão para hospedar-se na residência de Cardano, cuja promessa de apresentar o vice-rei mostra-se falaciosa. Para compensar o embuste, Cardano recebe Tartaglia com toda a hospitalidade e fidalguia possíveis, sem desistir de seu intento, solicitando ainda uma vez mais que o segredo de solução das cúbicas fosse revelado. Tartaglia, talvez lisonjeado com o tratamento recebido, enfim cede e aceita revelar sua fórmula, porém apenas mediante solene juramento, exigindo que Cardano jamais revelasse o método a ninguém, nem o publicasse. Girolamo assente a contragosto, proferindo o seguinte juramento:

Juro a você, pelas Sagradas Escrituras de Deus, e como verdadeiro homem honrado, não apenas jamais publicar suas descobertas se você me ensiná-las, como também prometo, e empenho minha fé como verdadeiro cristão, anotá-las em código, de forma que, após a minha morte, ninguém será capaz de entendê-las.

Não obstante, Tartaglia envia a resposta encriptada na forma de um poema, cujos versos (no original, em italiano) são os seguintes:

Quando che'l cubo con le cose appresso

se agguaglia a qualche numero discreto

trovan dui altri differenti in esso.

Da poi terrai questo per consueto

che il loro prodotto sempre sia eguale

al terzo cubo delle cose netto,

El residuo poi suo generale

delli lor lati cubi ben sottratti

varrà la tua cosa principale.

In el secondo dei codesti atti

quando che'l cubo restasse lui solo

tu osserverai quant'altri contratti.

Del numero farai due tal partà volo

che l'una in l'altra si produca schietto

el terzo cubo delle cose in stolo.

Dalla quale poi, per commun precetto

torra li lati cubi insieme gionti

et cotal somma sarà il tuo concetto.

El terzo poi de questi nostri conti

se solve col secondo se ben guardi

che per natura son quasi congianti.

Questi trovai, et non con passi tardi

nel mille cinqucente, quatro e trenta

con fondamenti ben saldi e gagliardi

Nella città dal mare intorno centa.

A tradução do poema para o português e sua equivalência matemática estão indicados abaixo:

Quando o cubo e a coisa juntos
correspondem a algum número discreto,	$$ x^{3}+px=q $$
encontre outros dois números subtraídos dele.	$$ u-v=q $$

Desde então, tenho mantido este costume
que o seu produto sempre deve ser igual
exatamente ao cubo de um terço da coisa.	$$ uv=\left ( \frac{p}{q} \right )^{3} $$

O resto, assim, como regra geral
de suas raízes cúbicas subtraídas
será igual à coisa principal.	$$ x=\sqrt[3]{u}-\sqrt[3]{v} $$

No segundo destes atos,
quando o cubo permanece sozinho	$$ x^{3}=px+q $$
observarás estes outros contratos:

Dividirás a um só tempo o número em duas partes	$$ q=u+v $$
de modo que um vezes o outro produza claramente
o cubo de um terço da coisa exatamente.	$$ uv=\frac{p^{3}}{3} $$

Então, destas duas partes, como regra habitual
tomarás as raízes cúbicas somadas entre si
e esta soma será sua reflexão.	$$ x=\sqrt[3]{u}+\sqrt[3]{v} $$

O terceiro destes cálculos	$$ x^{3}+q=px $$
é solucionado como no segundo se tomares bom cuidado,
pois em suas essências, estão quase equiparados.

Estas coisas encontrei, e não com passos vagarosos
no ano de mil quinhentos e trinta e quatro
com fundações fortes e resistentes
na cidade cercada pelo mar.	[Veneza]

Nas primeiras sete estrofes do poema, Tartaglia apresenta as soluções codificadas para as cúbicas do tipo:
$$ \left\{\begin{matrix}x^{3}+px=q\\ x^{3}=px+q\\ x^{3}+q=px\end{matrix}\right. $$
Fato é que Cardano consegue decifrar o poema de Tartaglia, ainda que tenha implorado, através de uma carta, que Tartaglia lhe explicasse como montar a equação com base no sexto e no décimo quinto versos que contêm, ambos, instruções dúbias. A solução encontrada por Cardano inicia-se com a equação cúbica geral abaixo:
$$ x^{3}+ax^{2}+bx+c=0 $$
Novamente, a, b e c são reais. A seguir, ele efetua a seguinte substituição:
$$ x=y-\frac{a}{3} $$
Com y a ser determinado, resultando na expressão abaixo:
$$ \left (y-\frac{a}{3} \right )^{3}+a\left (y-\frac{a}{3} \right )^{2}+b\left (y-\frac{a}{3} \right )+c=0 $$
Expandindo o polinômio:
$$ \left ( y^{3}-3y^{2}\frac{a}{3}+3y\frac{a^{2}}{9}-\frac{a^{3}}{27} \right )+a\left ( y^{2}-2y\frac{a}{3}+\frac{a^{2}}{9} \right )+b\left ( y-\frac{a}{3} \right )+c=0 $$
$$ \left ( y^{3}-y^{2}a+y\frac{a^{2}}{3}-\frac{a^{3}}{27} \right )+\left ( y^{2}a-2y\frac{a^{2}}{3}+\frac{a^{3}}{9} \right )+\left ( yb-b\frac{a}{3} \right )+c=0 $$
Agrupando os termos comuns:
$$ y^{3}+\left ( a-a \right )y^{2}+\left ( \frac{a^{2}}{3}-\frac{2a^{2}}{3}+b \right )y+\left ( \frac{a^{3}}{9}-\frac{a^{3}}{27}-\frac{ba}{3}+c \right )=0 $$
$$ y^{3}+\left ( -\frac{a^{2}}{3}+b \right )y=\left ( -\frac{2a^{3}}{27}+\frac{ba}{3}-c \right ) $$
Renomeando o segundo termo para:
$$ \left ( -\frac{a^{2}}{3}+b \right )=p $$
E renomeando o terceiro termo para:
$$ \left ( -\frac{2a^{3}}{27}+\frac{ba}{3}-c \right )=q $$
A equação cúbica geral fica reduzida a:
$$ y^{3}+py=q $$
Com a cúbica reduzida em mãos, Cardano lança mão de um cálculo volumétrico, agrupando cubos e paralelepípedos reais, certamente guiado pela prática árabe da “completude do quadrado” de Khwarizmi e pela “completude do cubo” de Khayyam; neste caso, u e v compõem os lados de um cubo completo:

Observe:

·	Volume do cubo rosa:	$$ v^{3} $$
·	Volume do cubo verde:	$$ \left ( u-v \right )^{3} $$
·	Volume do paralelepípedo incolor:	$$ uv\left ( u-v \right ) $$
·	Volume do paralelepípedo azul:	$$ uv\left ( u-v \right ) $$
·	Volume do paralelepípedo amarelo:	$$ v^{2}\left ( u-v \right ) $$
·	Volume do paralelepípedo vermelho:	$$ v\left ( u-v \right )^{2} $$

O volume total será igual à soma dos volumes parciais:

$$ u^{3}=v^{3}+\left ( u-v \right )^{3}+uv\left ( u-v \right )+uv\left ( u-v \right )+v^{2}\left ( u-v \right )+v\left ( u-v \right )^{2} $$

Resolvendo:
$$ u^{3}-v^{3}=\left ( u-v \right )^{3}+2uv\left ( u-v \right )+uv^{2}-v^{3}+v\left ( u^{2}-2uv+v^{2} \right ) $$
$$ u^{3}-v^{3}=\left ( u-v \right )^{3}+2u^{2}v-2uv^{2}+uv^{2}-v^{3}+u^{2}v-2uv^{2}+v^{3} $$
$$ u^{3}-v^{3}=\left ( u-v \right )^{3}+3u^{2}v-3uv^{2} $$
$$ u^{3}-v^{3}+3uv\left ( u-v \right )-\left ( u^{3}-v^{3} \right )=0 $$
Fazendo:
$$ y=u-v $$
A expressão cúbica anterior transforma-se em:
$$ y^{3}+3uvy-\left ( u^{3}-v^{3} \right )=0 $$
Novamente temos uma cúbica reduzida, ou seja, u – v é uma solução para:
$$ y^{3}+py+q=0 $$
Assim, fazendo:
$$ p=3uv $$
E:
$$ q=-\left ( u^{3}-v^{3} \right ) $$
Isolando-se v de p, vem:
$$ v=\frac{p}{3u} $$
Substituindo-se v em p na expressão com q:
$$ q=-u^{3}+\frac{p^{3}}{27u^{3}} $$
Multiplicando-se esta expressão por u³, vem:
$$ u^{3}q=-u^{6}+\frac{p^{3}}{27} $$
$$ u^{6}+u^{3}q-\frac{p^{3}}{27}=0 $$
Podendo ser reescrita como:
$$ \left ( u^{3} \right )^{2}+\left ( u^{3} \right )q-\frac{p^{3}}{27}=0 $$
Que é quadrática em u³, cuja solução é conhecida:
$$ u^{3}=\frac{q\pm \sqrt{q^{2}-4\times 1\times -\frac{p^{3}}{27}}}{2} $$
Simplificando a expressão acima, obtemos duas raízes:
$$ u_{1}^{3}=\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{2}} $$
$$ u_{2}^{3}=\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{2}} $$
Extraindo-se as raízes cúbicas:
$$ u_{1}=\sqrt[3]{\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{2}}} $$
$$ u_{2}=\sqrt[3]{\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{2}}} $$
Para encontrar o valor de v³, temos:
$$ q=\left ( u^{3}-v^{3} \right ) $$
$$ v^{3}=u^{3}-q $$
Encontrando-se, também, duas soluções:
$$ v_{1}^{3}=\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}-\left ( \frac{p}{3} \right )^{2}}-q=-\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}-\left ( \frac{p}{3} \right )^{2}} $$
$$ v_{2}^{3}=\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}-q=-\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}} $$
Extraindo-se as raízes cúbicas:
$$ v_{1}=\sqrt[3]{-\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}} $$
$$ v_{2}=\sqrt[3]{-\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}} $$
Assim, as soluções da cúbica reduzida serão:
$$ y=u_{1}-v_{1} $$
$$ v_{2}=\sqrt[3]{\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}}-\sqrt[3]{-\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}} $$
Ou ainda:
$$ y=u_{2}-v_{2} $$
$$ v_{2}=\sqrt[3]{\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}}-\sqrt[3]{-\frac{q}{2}-\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}} $$
A segunda solução gera números negativos, de modo que Cardano aceitava apenas a primeira solução como resposta de uma cúbica. Vejamos um exemplo de como utilizar esta fórmula, baseada nos versos de Tartaglia, através da equação cúbica abaixo:
$$ x^{3}+6x=20 $$
Como esta expressão já é uma cúbica reduzida, onde p = 6 e q = 20, bastará aplicar a primeira solução da cúbica, ou fórmula de Cardano para encontrar a raiz cúbica da equação:
$$ x=\sqrt[3]{\frac{20}{2}+\sqrt{\left ( \frac{20}{2} \right )^{2}+\left ( \frac{6}{3} \right )^{3}}}-\sqrt[3]{-\frac{20}{2}+\sqrt{\left ( \frac{20}{2} \right )^{2}+\left ( \frac{6}{3} \right )^{3}}} $$
$$ x=\sqrt[3]{10+\sqrt{\left ( 10 \right )^{2}+\left ( 2 \right )^{3}}}-\sqrt[3]{-10+\sqrt{\left ( 10 \right )^{2}+\left ( 2 \right )^{3}}} $$
$$ x=\sqrt[3]{10+\sqrt{108}}-\sqrt[3]{-10+\sqrt{108}} $$
Finalmente, chega-se ao resultado:
$$ x=\sqrt[3]{10+6\sqrt{3}}-\sqrt[3]{-10+6\sqrt{3}} $$
Se calcularmos as raízes quadradas e cúbicas da resposta acima, chegaremos à conclusão de que x vale rigorosamente 2, algo que Cardano também observou, mas não foi capaz de provar. Outra situação com que ele se defronta é que sua fórmula às vezes gerava raízes quadradas de números negativos, algo insolúvel e sem significado naquela época. Uma das equações estudadas pelo matemático que conduz a esse resultado está indicada abaixo:
$$ x^{3}-15x=4 $$
Onde p = –15 e q = 4. Aplicando a fórmula, obtemos:
$$ x=\sqrt[3]{\frac{4}{2}+\sqrt{\left ( \frac{4}{2} \right )^{2}+\left ( \frac{-15}{3} \right )^{3}}}-\sqrt[3]{-\frac{4}{2}+\sqrt{\left ( \frac{4}{2} \right )^{2}+\left ( \frac{-15}{3} \right )^{3}}} $$
$$ x=\sqrt[3]{2+\sqrt{\left ( 2 \right )^{2}+\left ( -5 \right )^{3}}}-\sqrt[3]{-2+\sqrt{\left ( 2 \right )^{2}+\left ( -5 \right )^{3}}} $$
$$ x=\sqrt[3]{2+\sqrt{-121}}-\sqrt[3]{-2+\sqrt{-121}} $$

Por conta destes resultados com raízes quadradas negativas, em 4 de Agosto de 1.539 Cardano escreve outra carta a Tartaglia que começa com o seguinte teor:

Venho por meio desta questioná-lo, após a solução de vários problemas para os quais não me destes nenhuma resposta, um dos quais diz respeito ao cubo igual a uma incógnita mais um número. Tenho a certeza de que compreendi esta regra, mas quando o cubo de um terço da incógnita é maior em valor que o quadrado da metade do número, então, ao que parece, não consigo ajustá-los à fórmula.

Tartaglia tampouco conhecia os números complexos e a esta altura encontrava-se já muito arrependido por ter ensinado sua fórmula a Cardano, de modo que tentou confundí-lo nestes termos:

... e por isso digo-te em resposta que ainda não dominastes o verdadeiro método para solucionar problemas deste tipo, e de fato diria que teus métodos são totalmente falsos.

Mesmo com as tentativas de Tartaglia de confundir Cardano e Ferrari, a verdade é que essa dupla fez progressos notáveis e tiveram até uma ajudinha do pertinaz Zuanne Tonini da Coi quando este, em 1.540, importuna Cardano propondo-lhe o seguinte problema (que até então ninguém havia solucionado, e do qual – julgavam os matemáticos – fosse insolúvel):

Encontre-me três números, em proporção contínua, dos quais a soma seja dez e o produto do segundo pelo terceiro seja seis.

Este problema colocado em termos matemáticos:

$$ \left\{\begin{matrix}\frac{x}{z}=\frac{z}{y}\\ x+y+z=10\\ y\times z=6\end{matrix}\right. $$

E desenvolvido, conduz à problemática equação quártica:

$$ y^{4}+6y^{2}+36=60y $$

Depois de desistir de encontrar uma solução, Cardano entrega o problema a Ferrari, que em 1.540, de forma brilhante, com um belo argumento algébrico e utilizando radicais, descobre a solução geral das equações quárticas. A abordagem utilizada por Ferrari é indicada a seguir. Do mesmo modo que para equações quadráticas e cúbicas, uma equação quártica geral qualquer:

$$ ax^{4}+bx^{3}+cx^{2}+dx+e=0 $$

Poderá ser simplificada, de modo a eliminar o seu termo cúbico (ou seja, o x³), gerando uma nova equação quártica reduzida. Sendo a, b, c, d e e reais, com a diferente de zero e fazendo:

$$ x=y+z $$

Com z a ser determinado, substituindo na quártica geral, vem:

$$ a\left ( y+z \right )^{4}+b\left ( y+z \right )^{3}+c\left ( y+z \right )^{2}+d\left ( y+z \right )+e=0 $$

Expandindo os polinômios, temos:

$$ \left ( y+z \right )^{4}=\left ( y^{4}+4y^{3}z+6y^{2}z^{2}+4yz^{3}+z^{4} \right ) $$

$$ \left ( y+z \right )^{3}=\left ( y^{3}+3y^{2}z+3yz^{2}+z^{3} \right ) $$

$$ \left ( y+z \right )^{2}=\left ( y^{2}+2yz+z^{2} \right ) $$

Multiplicando pelas respectivas constantes:

$$ a\left ( y^{4}+4y^{3}z+6y^{2}z^{2}+4yz^{3}+z^{4} \right )=ay^{4}+4ay^{3}z+6ay^{2}z^{2}+4ayz^{3}+az^{4} $$

$$ b\left ( y^{3}+3y^{2}z+3yz^{2}+z^{3} \right )=by^{3}+3by^{2}z+3byz^{2}+bz^{3} $$

$$ c\left ( y^{2}+2yz+z^{2} \right )=cy^{2}+2cyz+cz^{2} $$

$$ d\left ( x+y \right )=dx+dy $$

Agrupando os termos comuns:

$$ ay^{4} $$

$$ \left ( 4az+b \right )y^{3} $$

$$ \left ( 6az^{2}+3bz+c \right )y^{2} $$

$$ \left ( 4az^{3}+3bz^{2}+2cz+d \right )y $$

$$ \left ( az^{4}+bz^{3}+cz^{2}+dz+e \right ) $$

Impondo que:

$$ \left ( 4az+b \right )=0 $$

Isolando z desta equação resulta:

$$ z=\frac{-b}{4a} $$

O primeiro par de parênteses do polinômio expandido (que está sendo multiplicado por y³) é nulo. A substituição do valor de z no segundo par de parênteses da equação com os termos comuns agrupados fornece:

$$ \left ( 6az^{2}+3bz+c \right ) $$

$$ \left ( 6a\left ( \frac{-b}{4a} \right )^{2}+3b\left ( \frac{-b}{4a} \right )+c \right ) $$

$$ \left ( 6a\frac{b^{2}}{16a^{2}}-\frac{3b^{2}}{4a}+c \right ) $$

$$ \left ( \frac{3b^{2}}{8a}-\frac{3b^{2}}{4a}+c \right ) $$

$$ \left ( \frac{-3b^{2}}{8a}+c \right ) $$

E a substituição do valor de z no terceiro par de parênteses da equação com os termos comuns agrupados fornece:

$$ \left ( 4az^{3}+3bz^{2}+2cz+d \right ) $$

$$ 4a\left ( \frac{-b}{4a} \right )^{3}+3b\left ( \frac{-b}{4a} \right )^{2}+2c\left ( \frac{-b}{4a} \right )+d $$

$$ 4a\left ( \frac{-b^{3}}{64a^{3}} \right )+3b\left ( \frac{b^{2}}{16a^{2}} \right )+2c\left ( \frac{-b}{4a} \right )+d $$

$$ \left ( \frac{-b^{3}}{16a^{2}} \right )+\left ( \frac{3b^{3}}{16a^{2}} \right )-2c\left ( \frac{b}{4a} \right )+d $$

$$ \left ( \frac{-b^{3}}{16a^{2}}+\frac{3b^{3}}{16a^{2}} \right )-2c\left ( \frac{b}{4a} \right )+d $$

$$ \left ( \frac{2b^{3}}{16a^{2}}-\frac{cb}{2a}+d \right ) $$

Assim, a equação quártica fica modificada conforme abaixo:

$$ ay^{4}+\left ( \frac{-3b^{2}}{8a}+c \right )y^{2}+\left ( \frac{2b^{3}}{16a^{2}}-\frac{cb}{2a}+d \right )y+\left ( az^{4}+bz^{3}+cz^{2}+dz+e \right )=0 $$

Por fim, multiplicando toda a equação por 1/a resulta:

$$ y^{4}+\left ( \frac{-3b^{2}}{8a^{2}}+\frac{c}{a} \right )y^{2}+\left ( \frac{2b^{3}}{16a^{3}}-\frac{cb}{2a^{2}}+\frac{d}{a} \right )y+\left ( z^{4}+\frac{bz^{3}}{a}+\frac{cz^{2}}{a}+\frac{dz}{a}+\frac{e}{a} \right )=0 $$

Renomeando o segundo termo para:

$$ \left ( \frac{-3b^{2}}{8a^{2}}+\frac{c}{a} \right )=p $$

Renomeando o terceiro termo para:

$$ \left ( \frac{2b^{3}}{16a^{3}}-\frac{cb}{2a^{2}}+\frac{d}{a} \right )=q $$

E renomeando o quarto termo para:

$$ \left (z^{4}+\frac{bz^{3}}{a}+\frac{cz^{2}}{a}+\frac{dz}{a}+\frac{e}{a} \right )=r $$

A equação quártica geral fica reduzida a:

$$ y^{4}+py^{2}+qy+r=0 $$

Para resolver esta quártica reduzida, Ferrari a reescreveu como:

$$ y^{4}+py^{2}=-qy-r $$

Em seguida, ele somou py² + p² em ambos os lados da equação para obter, do lado esquerdo, um binômio quadrado perfeito:

$$ y^{4}+py^{2}+py{2}+p^{2}=-qy-r+py^{2}+p^{2} $$

$$ y^{4}+2py^{2}+p^{2}=py^{2}-qy+p^{2}-r $$

$$ \left (y^{2}+p \right )^{2}=py^{2}-qy+p^{2}-r $$

O toque de genialidade de Ferrari começa quando introduz uma nova variável, t, a ser determinada posteriormente, somando-a dentro do binômio quadrado perfeito:

$$ \left (y^{2}+p+t \right )^{2}=py^{2}-qy+p^{2}-r $$

Expandindo o agora trinômio, temos:

$$ \left (y^{2}+p+t \right )^{2}=\left (y^{2}+p+t \right )\times \left (y^{2}+p+t \right ) $$

$$ y^{4}+2py^{2}+p^{2}+2y^{2}t+2pt+t^{2} $$

Mas observe que após esta operação, temos novamente entre parênteses os termos do binômio quadrado perfeito:

$$ \left (y^{4}+2py^{2}+p^{2} \right )+2y^{2}t+2pt+t^{2} $$

$$ \left (y^{2}+p \right )^{2}+2y^{2}t+2pt+t^{2} $$

Ou seja: somar t dentro do binômio teria sido o mesmo que somar ao binômio (y² + p)² a expressão:

$$ 2y^{2}t+2pt+t^{2} $$

Logo, para manter a igualdade, a expressão acima será somada no lado direito da equação:

$$ \left ( y^{2}+p+t \right )^{2}=\left ( py^{2}-qy+p^{2}-r \right )+2y^{2}t+2pt+t^{2} $$

Agrupando os termos do lado direito da equação, obtém-se:

$$ \left ( y^{2}+p+t \right )^{2}=\left ( p+2t \right )y^{2}-qy+\left ( p^{2}-r+2pt+t^{2} \right ) $$

O desafio passa a ser a busca de um valor para t de modo que o lado direito da equação também forme um binômio quadrado perfeito, uma vez que, agora, já conseguimos formar desse lado uma equação quadrática. Para isso, a equação quadrática do lado direito da igualdade tem que assumir a forma do binômio abaixo:

$$ \left [ \left ( \sqrt{p+2t} \right )y\pm \sqrt{p^{2}-r+2pt+t^{2}} \right ]^{2} $$

A razão é simples. Ao expandirmos esse binômio, chega-se a:

$$ \left ( p+2t \right )y^{2}\pm \left ( 2\sqrt{p+2t}\sqrt{p^{2}-r+2pt+t^{2}} \right )y+\left ( p^{2}-r+2pt+t^{2} \right ) $$

Observe: o termo –q, que aparentemente havia desaparecido do binômio, na verdade equivale a:

$$ -q=\pm \left ( 2\sqrt{p+2t}\sqrt{p^{2}-r+2pt+t^{2}} \right ) $$

Elevando esta expressão ao quadrado:

$$ q^{2}=4\left ( p+2t \right )\left ( p^{2}-r+2pt+t^{2} \right ) $$

[7]

Expandindo e reagrupando em função de t, temos:

$$ 8t^{3}+20pt^{2}+\left ( 16p^{2}-8r \right )t+\left ( 4p^{3}-4pr-q^{2} \right )=0 $$

Chegamos a uma expressão cúbica geral em t. De fato, fora comentado que o valor de t seria determinado posteriormente: este é o momento. Reduzindo a cúbica geral e utilizando a expressão de Cardano, Ferrari encontra o valor de t, pois os valores das constantes p, q e r são conhecidos:

$$ \left ( \frac{-3b^{2}}{8a^{2}}+\frac{c}{a} \right )=p $$

$$ \left ( \frac{2b^{3}}{16a^{3}}-\frac{cb}{2a^{2}}+\frac{d}{a} \right )=q $$

$$ \left ( z^{4}+\frac{bz^{3}}{a}+\frac{cz^{2}}{a}+\frac{dz}{a}+\frac{e}{a} \right )=r $$

O valor de z também havia sido determinado e vale:

$$ z=\frac{-b}{4a} $$

Sendo que os valores das constantes a, b, c, d e e constam da equação quártica geral, que obviamente são fornecidos. Assim, considerando-se que o valor de t tenha sido determinado, então finalmente o lado direito da expressão:

$$ \left ( y^{2}+p+t \right )^{2}=\left ( p+2t \right )y^{2}-qy+\left ( p^{2}-r+2pt+t^{2} \right ) $$

Formará o almejado binômio quadrado perfeito:

$$ \left ( y^{2}+p+t \right )^{2}=\left [ \left ( \sqrt{p+2t} \right )y\pm \sqrt{p^{2}-r+2pt+t^{2}} \right ]^{2} $$

Agora que temos quadrados perfeitos em ambos os lados da igualdade, extrai-se a raiz quadrada destas expressões:

$$ \left ( y^{2}+p+t \right )=\pm \left [ \left ( \sqrt{p+2t} \right )y\pm \sqrt{p^{2}-r+2pt+t^{2}} \right ] $$

[8]

A equação [8] é a fórmula de Ferrari e o resultado de seu brilhante e criativo exercício algébrico. Note que a fórmula apresenta quatro soluções, ou raízes, como indicado pelos sinais ±. Parte de sua genial argumentação, porém, baseia-se na solução de Tartaglia e, em função do juramento prestado por Cardano e sem poder quebrá-lo, não poderia tornar-se pública. Porém, aos poucos, Cardano deve ter percebido que Del Fiore não teria desafiado Tartaglia para uma contenda matemática anos antes se não conhecesse uma fórmula para resolver equações cúbicas, mesmo não sendo um matemático talentoso e, portanto, deve ter concluído que Del Ferro (professor de Del Fiore) a tivesse descoberto ou soubesse de algo importante sobre esse assunto, além do próprio Tartaglia. Assim, em 1.543, Cardano e Ferrari decidem viajar até Bolonha e visitar seu colega Della Nave. É Ferrari quem comenta sobre esta passagem, em Abril de 1.547:

Quatro anos atrás, quando Cardano dirigiu-se à Florença e eu o fiz acompanhar, encontramo-nos em Bolonha com Aníbal Della Nave, um homem inteligente e humano que nos mostrou uma pequena caderneta outrora pertencente a Del Ferro, seu sogro, escrita muito tempo atrás, na qual aquela descoberta [fórmula das cúbicas] é apresentada com elegância e eruditismo.

De fato, Cardano e Ferrari satisfizeram a curiosidade de Della Nave, mostrando-lhe que eram capazes de resolver o onipresente problema da coisa e cubo, ou seja, a quártica; em troca, Della Nave lhes mostra a caderneta de anotações do sogro, de que detinha a posse. Percebendo que Del Ferro chegara à solução das cúbicas de forma independente cerca de 20 anos antes do próprio Tartaglia, Cardano considerou sem valor o juramento que lhe fizera. Livre de tal compromisso, em 1.545 publica uma das grandes obras de matemática: o Ars Magna (A Grande Arte). Em edições posteriores aparece também com o nome Artis Magnæ. Apesar de Cardano citar Tartaglia nominalmente como tendo descoberto de forma independente de Del Ferro a solução das cúbicas em duas passagens distintas em seu livro, fato é que Tartaglia nunca o perdoou por ter quebrado o seu juramento e divulgado a sua fórmula, talvez porque soubesse que com essas descobertas era Cardano quem entraria para a história e não ele. Seja como for, vejamos um exemplo de solução de uma equação quártica reduzida apresentada no Ars Magna:

$$ x^{4}-12x+3=0 $$

Note que esta quártica reduzida, além da ausência do termo x³, também não possui o termo quadrático x². Nestas condições, temos:

$$ p=0 $$

$$ q=-12 $$

$$ r=3 $$

Fazendo uso da equação cúbica [7], vem:

$$ q^{2}=4\left ( p+2t \right )\left ( p^{2}-r+2pt+t^{2} \right ) $$

$$ \left ( -12 \right )^{2}=4\left ( 0+2t \right )\left ( 0^{2}-3+2.0.t+t^{2} \right ) $$

$$ 144=8t\left ( -3+t^{2} \right ) $$

$$ 8t^{3}-24t=144 $$

Simplificando, chega-se finalmente a:

$$ t^{3}-3t=18 $$

Fazendo p = –3 e q = 18 e aplicando a fórmula de Cardano para encontrar a raíz cúbica positiva, temos:
$$ t=\sqrt[3]{\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}}-\sqrt[3]{-\frac{q}{2}+\sqrt{\left ( \frac{q}{2} \right )^{2}+\left ( \frac{p}{3} \right )^{3}}} $$
$$ t=\sqrt[3]{\frac{18}{2}+\sqrt{\left ( \frac{18}{2} \right )^{2}+\left ( \frac{-3}{3} \right )^{3}}}-\sqrt[3]{-\frac{18}{2}+\sqrt{\left ( \frac{18}{2} \right )^{2}+\left ( \frac{-3}{3} \right )^{3}}} $$
$$ t=\sqrt[3]{9+\sqrt{\left ( 9 \right )^{2}+\left ( -1 \right )^{3}}}-\sqrt[3]{-9+\sqrt{\left ( 9 \right )^{2}+\left ( -1 \right )^{3}}} $$
$$ t=\sqrt[3]{9+\sqrt{80}}-\sqrt[3]{-9+\sqrt{80}} $$
$$ t=\sqrt[3]{9+4\sqrt{4}}-\sqrt[3]{-9+4\sqrt{5}} $$
$$ t=3 $$
Substituindo agora o valor de t na quártica de Ferrari, temos:
$$ \left ( y^{2}+p+t \right )=\pm \left [ \left ( \sqrt{p+2t} \right )y\pm \sqrt{p^{2}-r+2pt+t^{2}} \right ] $$
$$ \left ( y^{2}+0+3 \right )=\pm \left [ \left ( \sqrt{0+2.3} \right )y\pm \sqrt{0^{2}-3+2.0.3+3^{2}} \right ] $$
$$ \left ( y^{2}+3 \right )=\pm \left [ \left ( \sqrt{6} \right )y\pm \sqrt{-3+9} \right ] $$
$$ \left ( y^{2}+3 \right )=\pm \left [ \left ( \sqrt{6} \right )y\pm \sqrt{6} \right ] $$
Chegando-se às quatro equações quadráticas:
$$ \left\{\begin{matrix}y^{2}-\left ( \sqrt{6} \right )y+\left ( 3-\sqrt{6} \right )=0\\ y^{2}-\left ( \sqrt{6} \right )y+\left ( 3+\sqrt{6} \right )=0\\ y^{2}+\left ( \sqrt{6} \right )y+\left ( 3-\sqrt{6} \right )=0\\ y^{2}+\left ( \sqrt{6} \right )y+\left ( 3+\sqrt{6} \right )=0\end{matrix}\right. $$
Resolvendo a primeira das quatro equações por Báskara, temos:
$$ y=\frac{\sqrt{6}\pm \sqrt{\left ( -\sqrt{6} \right )^{2}-4\times 1\times \left ( 3-\sqrt{6} \right )}}{2\times 1} $$
$$ y=\frac{\sqrt{6}\pm \sqrt{6-12+4\sqrt{6}}}{2} $$
$$ y=\frac{\sqrt{6}\pm \sqrt{-6+4\sqrt{6}}}{2} $$
De modo análogo, a segunda equação fornece:
$$ y=\frac{\sqrt{6}\pm \sqrt{-6-4\sqrt{6}}}{2} $$
A terceira equação fornece:
$$ y=\frac{-\sqrt{6}\pm \sqrt{-6+4\sqrt{6}}}{2} $$
E a quarta equação fornece:
$$ y=\frac{-\sqrt{6}\pm \sqrt{-6-4\sqrt{6}}}{2} $$

Sendo que somente a primeira e a terceira respostas eram consideradas válidas no Ars Magna, já que a segunda e a quarta respostas continham raízes quadradas de números negativos, gerando números complexos, não conhecidos por Cardano. Apesar dos exemplos relativamente complexos envolvendo as equações cúbicas e quárticas apresentadas no Ars Magna, é possível (ao menos para as cúbicas) a proposição de problemas cujo enunciado e respectiva solução tenham algum significado ou utilidade prática. É o caso, por exemplo, do problema geométrico constante na Proposição IV do Livro II da obra Da Esfera e do cilindro, de Arquimedes, que o estudou, mas que foi incapaz de resolvê-lo por completo, alegando haver um diorismos. Diorismos é um termo técnico grego que no contexto indica limites para os quais o problema possui uma solução, cujo enunciado – adaptado[3] – é o seguinte:

Cortar uma dada esfera por um plano de modo que os volumes obtidos pelos dois segmentos formados estejam em uma dada razão.

[3] O enunciado original é este: Cortar a esfera dada, de modo que os seus segmentos guardem entre si a mesma razão dada.

O problema pode ser reduzido a uma forma ainda mais simples que a apresentada no enunciado, conforme abaixo:

Cortar um segmento de reta dado, de comprimento a, em duas partes, tais que o primeiro segmento, de comprimento x, multiplicado pelo segundo segmento, de comprimento (a – x), igualem-se a um dado volume c.

Foi o matemático persa Muhammad ibn Isa al-Mahani que, por volta de 850 d.C. em Bagdá, obteve sucesso na conversão do problema em uma equação algébrica cúbica:

$$ x^{3}+c=ax^{2} $$

E no século seguinte esta equação foi resolvida através de seções cônicas. Porém, em 1.290 d.C., outro matemático persa – Sharaf al-Din al-Tusi – também em Bagdá, foi além ao indagar-se quão grande poderia ser esse volume c e ainda admitir a existência de uma solução. A proposição é a seguinte:

Sami é um funcionário de manutenção de um hospital em Bagdá. Foi-lhe solicitado encobrir com cortinas uma área ao redor da cama de um paciente, por privacidade. A cama fica no canto de uma ala, de modo que a cortina precisa proteger apenas dois de seus lados: haverá uma cortina quadrada protegendo o lado comprido da cama e uma cortina retangular menor cobrindo o pé da cama. As duas cortinas serão penduradas em hastes, suspensas a igual distância do teto da enfermaria. Mas é aí que Sami enfrenta um problema: por causa da guerra e da falta de suprimentos em Bagdá, o único material disponível para montar as hastes é uma vara de madeira de seis metros, que ele pode cortar como quiser para obter as duas hastes onde serão penduradas as cortinas. Sami deseja saber qual o maior volume retangular que será capaz de obter com essas hastes.

A figura a seguir ilustra o problema de Sami:

A disposição das cortinas ao redor da cama

O problema impõe algumas restrições: uma das cortinas é quadrada, e o tamanho da vara para montar os dois suportes é de apenas seis metros. Da figura acima, o volume do espaço privado é calculado como:

$$ Volume=x^{2}\times y $$

E a restrição entre as larguras das cortinas (que, somadas, não podem exceder os seis metros) será dada por:

$$ y=6-x $$

Onde x corresponde às dimensões da cortina quadrada bem como à altura da cortina retangular (já que ambas devem ter a mesma altura) e y corresponde à largura da cortina retangular. Observe ainda que não é especificada nenhuma limitação quanto a altura mínima ou máxima que essas cortinas podem ter. Assim, para calcular o máximo volume possível, montamos a tabela abaixo:

x (m)	x² (m²)	y (m)	Volume (m³)
0	0	6	0
1	1	5	5
2	4	4	16
3	9	3	27
4	16	2	32
5	25	1	25
6	36	0	0

Observe: a primeira coluna apresenta as possíveis dimensões da cortina quadrada e a altura da cortina retangular, começando de zero metro (o que na prática não tem significado) até seis metros, que corresponde ao tamanho total da vara. Na segunda coluna, temos a área da cortina quadrada. Na terceira coluna, temos a largura da cortina retangular, que corresponde ao tamanho total da vara (seis metros) menos o valor de x. Finalmente, na quarta e última coluna temos o volume total obtido. A linha destacada em laranja indica o maior volume possível, que é obtido com:

· Uma cortina quadrada de 4 metros de altura por 4 metros de largura;

· Uma cortina retangular de 4 metros de altura por 2 metros de largura.

Se montássemos um gráfico com base nos valores de x e do volume, obteríamos:

Concluímos, com este exemplo prático, o estudo das origens das equações algébricas do 3° e do 4° graus.

Referências bibliográficas:

[1]	Khayyam, O. “Os Rubayat”, tradução para o português por Alfredo Braga, disponível no sítio: http://alfredo-braga.pro.br/poesia/rubaiyat.html. Acessado em Dezembro/2017.
[2]	Mardia, K. V. “Omar Khayyam, René Descartes and solutions to algebraic equations”, paper presented to Omar Khayyam Club, London, 1999.
[3]	Kent, D. A.; Muraki, D. J. “A geometric solution of a cubic by Omar Khayyam… in which coloured diagrams are used instead of letters for the greater ease of learners”, American Mathematical Monthly 121:1, May 2015.
[4]	Henderson, D. W. “Geometric solutions to quadratic and cubic equations”, Department of Mathematics, Cornell University. Acessado em Dez/2017: www.math.cornell.edu/~dwh/papers/geomsolu/geomsolu.html
[5]	Brown, E.; Brunson, J. C. “Fibonacci’s forgotten number”, The College Mathematics Journal, Vol. 39, No. 2, March 2008.
[6]	Well, D. “The Penguin book of curious and interesting puzzles”, Penguin Books, 1992.
[7]	Franci, R.; Rigatelli, L. T. “Maestro Benedetto da Firenze e la storia dell’algebra”, Historia Mathematica 10, pags. 297-313, 1983.
[8]	Franci, R. “Antonio de Mazzinghi: An algebraist of the 14th century”, Historia Mathematica 5, pags. 240-249, 1988.
[9]	Guilbeau, L. “The history of the solution of the cubic equation”, Mathematics News Letter, Vol. 5, No. 4, pags. 8-12, 1930.
[10]	Santos, S. R. “As equações polinomiais do 3° e 4° graus – Sua história e suas soluções”, dissertação de mestrado profissional em matemática, Universidade Federal de Sergipe, 2013.
[11]	Anderson, M.; Katz, V.; Wilson, R. “Sherlock Holmes in Babylon: And Other Tales of Mathematical History”, Mathematical Association of America, 2004. ISBN: 0-8838-5546-1, 978-0-8838-5546-1.
[12]	Contreras, J. N. “An Episode of the Story of the Cubic Equation: The del Ferro-Tartaglia-Cardano’s Formulas”, Journal of Mathematical Sciences & Mathematics Education, Volume 10, No. 2, pags. 24-37, 2015.
[13]	Glaz, S. “Poetry inspired by mathematics: a brief journey through history”, Journal of Mathematics and the Arts, Vol. 5, No. 4, pags. 171-183, 2011.
[14]	Katscher, F. “How Tartaglia solved the cubic equation – Tartaglia’s poem”, Convergence, MAA Press, August 2011.
[15]	Roberts Jr., C. E. “Introduction to mathematical proofs – a transition to advanced mathematics”, Second Edition, CRC Press, 2015. ISBN-13: 978-1-4822-4688-9.
[16]	Morley, H. “Jerome Cardan: The life of Girolamo Cardano, of Milan, physician, Volumes 1-2”, Chapman and Hall, 1854.
[17]	Netz, R. “The works of Archimedes – Translation and commentary. Volume 1: The two books On the sphere and the cylinder”, Stanford University, 2009. ISBN-13: 978-0-5211-1798-2.

Ler mais »

quinta-feira, outubro 18, 2018

Equações algébricas do 3° e 4° graus

Matemática no youtube

Recentes

Destaques

Páginas deste blog

Arquivo de postagens

Postagens mais visitadas

Postagem em destaque

Equações algébricas do 3° e 4° graus

Tags