|
| Fractal de Mandelbrot |
$$ 23\left ( rolos-pimenta \right )=10\frac{58}{77}\left ( libras-acafrao \right ) $$
Se um mercador que tivesse os rolos de pimenta
quisesse trocá-las por açafrão com outro mercador, ele teria que saber quanto
vale, em frações de libra, a quantia 58/77. Como dito anteriormente, um
comerciante que não entendesse de regra de três, e de modo geral de contas,
poderia facilmente ser ludibriado quanto à quantia correta que 58/77
corresponde em peso de açafrão. Mesmo alguém acostumado a contas seria obrigado
a algum tipo de simplificação. Por exemplo, 58 está bem próximo de 60, assim
como 77 está bem próximo de 80. A nova fração resultante (60/80), ainda que não
tenha exatamente o mesmo valor da fração original, tem um valor aproximado e é
mais fácil de simplificar. De fato:
$$ \frac{60\div 10}{80\div 10}=\frac{6}{8}=\frac{6\div 2}{8\div 2}=\frac{3}{4} $$
A fração irredutível 3/4 é um número cujo valor compreende-se facilmente: ela nos diz que de uma libra de açafrão dividida em 4 partes iguais, tomam-se 3 partes. Assim, o mercador de pimentas receberia 10 libras mais 3/4 de uma libra de açafrão pelos 23 rolos de pimenta. Essa simplificação pode ser aceitável em trocas de mercadorias, mas certamente seria rejeitada pelos banqueiros medievais quando tivessem que converter imperiais em barcelonenses, de acordo com o outro exemplo de Fibonacci. De fato, 15 imperiais valiam, segundo a conversão apresentada:
A fração irredutível 3/4 é um número cujo valor compreende-se facilmente: ela nos diz que de uma libra de açafrão dividida em 4 partes iguais, tomam-se 3 partes. Assim, o mercador de pimentas receberia 10 libras mais 3/4 de uma libra de açafrão pelos 23 rolos de pimenta. Essa simplificação pode ser aceitável em trocas de mercadorias, mas certamente seria rejeitada pelos banqueiros medievais quando tivessem que converter imperiais em barcelonenses, de acordo com o outro exemplo de Fibonacci. De fato, 15 imperiais valiam, segundo a conversão apresentada:
$$ 20\frac{1.180}{3.298}barcelonenses $$
Aqui, depara-se com situação delicada: se considerarmos que a fração 1180/3298 possa ser substituída por outra fração com um valor aproximado, por exemplo: 1100/3300, então a nova fração irredutível resultante será: 1/3, de fácil compreensão e simples de cambiar. Porém, 1180 está mais próximo de 1200 que de 1100, de modo que podemos obter outra fração de valor aproximado à fração original: 1200/3300, ou ainda na fração irredutível equivalente: 4/11. Em termos absolutos, percebe-se que 1200/3300 está mais próximo de 1180/3298 que 1100/3300. Em outras palavras, se um mercador que tivesse 15 imperiais aceitasse de um banqueiro a conversão baseada em 20 barcelonenses mais a fração 1100/3300, o banqueiro sairia ganhando e faria a conversão com prazer. Do contrário, se o mercador exigisse que a conversão fosse feita com base em 20 barcelonenses mais a fração 1200/3300, o banqueiro devolveria os 15 imperiais se essa conversão lhe resultasse em prejuízo. Neste jogo de conversões ninguém quer perder, mas geralmente perdia quem tivesse menor poder de barganha, neste caso, o mercador... Eis o problema das frações: elas representam um número não inteiro muitas vezes difícil de quantificar. Significa, portanto, que a notação matemática representada pelas frações muitas vezes é insuficiente para expressar a idéia de valoração que lhe é subjacente. A transformação gradual das frações em números decimais é um caso interessante de evolução da notação matemática. Vejamos o exemplo a seguir:
Aqui, depara-se com situação delicada: se considerarmos que a fração 1180/3298 possa ser substituída por outra fração com um valor aproximado, por exemplo: 1100/3300, então a nova fração irredutível resultante será: 1/3, de fácil compreensão e simples de cambiar. Porém, 1180 está mais próximo de 1200 que de 1100, de modo que podemos obter outra fração de valor aproximado à fração original: 1200/3300, ou ainda na fração irredutível equivalente: 4/11. Em termos absolutos, percebe-se que 1200/3300 está mais próximo de 1180/3298 que 1100/3300. Em outras palavras, se um mercador que tivesse 15 imperiais aceitasse de um banqueiro a conversão baseada em 20 barcelonenses mais a fração 1100/3300, o banqueiro sairia ganhando e faria a conversão com prazer. Do contrário, se o mercador exigisse que a conversão fosse feita com base em 20 barcelonenses mais a fração 1200/3300, o banqueiro devolveria os 15 imperiais se essa conversão lhe resultasse em prejuízo. Neste jogo de conversões ninguém quer perder, mas geralmente perdia quem tivesse menor poder de barganha, neste caso, o mercador... Eis o problema das frações: elas representam um número não inteiro muitas vezes difícil de quantificar. Significa, portanto, que a notação matemática representada pelas frações muitas vezes é insuficiente para expressar a idéia de valoração que lhe é subjacente. A transformação gradual das frações em números decimais é um caso interessante de evolução da notação matemática. Vejamos o exemplo a seguir:
$$ 20\frac{1.180}{3.298} $$
Esta notação simboliza um número constituído de duas partes: uma inteira, representada pelo número 20, e outra fracionária, menor que 1, representada pela fração 1180/3298. Atribui-se aos chineses a primazia pelo uso de frações decimais no século I a.C. O sistema numérico chinês desse período, conhecido como numerais de varas, está indicado a seguir:
Nos primórdios desse sistema numérico, os zeros eram representados por espaços em branco; foi somente com o matemático Qin Jiushao que se introduziu o numeral zero na China, por meio de sua obra: Tratado matemático em nove seções, de 1.247. Assim, para Jiushao, o número 0,96644 seria representado como:
Supõe-se que o sistema decimal chinês tenha se espalhado por todo o Oriente Médio, influenciando os matemáticos árabes. O uso mais remoto de frações decimais entre os árabes aparece com os trabalhos do matemático e engenheiro al-Karaji (~953 a ~1029 d.C.): o Al-Badi' fi'l-hisab ("O maravilhoso livro de cálculo"), o Al-Fakhri fi'l-jabr wa'l-muqabala ("O glorioso livro de álgebra") e o Al-Kafi fi'l-hisab ("O livro suficiente de aritmética"). Seguindo a tradição de al-Karaji, o matemático al-Samawal (~1130 a ~1180 d.C.) utiliza as frações decimais em sua obra Al-Bahir fi'l-jabr ("O brilhante livro de álgebra"). Mas foi o matemático al-Kashi (1380 a 1429 d.C.) que ganhou fama ao aplicar uma notação decimal em seus estudos; é dele o tratado Miftah al-Hisab ("A chave para a aritmética"), de 1.427, em que calcula o número π (pi) com uma precisão de nove casas sexagesimais, equivalente a dezessete casas decimais, um feito que só seria superado pelo matemático alemão Ludolph van Ceulen em 1.596, quando alcançou uma precisão de 35 casas decimais para o cálculo do π que, entretanto, não é um número racional.
O matemático que talvez mais tenha contribuído para o desenvolvimento de uma notação decimal foi o belga Simon Stevin, quando publica um livreto especificamente sobre o assunto, chamado De Thiende (Os Décimos), em 1.585.
Na notação de Stevin, a fração mista:
Seria decomposta em uma soma de frações de potências de dez:
Esta notação simboliza um número constituído de duas partes: uma inteira, representada pelo número 20, e outra fracionária, menor que 1, representada pela fração 1180/3298. Atribui-se aos chineses a primazia pelo uso de frações decimais no século I a.C. O sistema numérico chinês desse período, conhecido como numerais de varas, está indicado a seguir:
 |
| Sistema numérico da antiga China. Linha superior: representação vertical; linha inferior: representação horizontal. |
Supõe-se que o sistema decimal chinês tenha se espalhado por todo o Oriente Médio, influenciando os matemáticos árabes. O uso mais remoto de frações decimais entre os árabes aparece com os trabalhos do matemático e engenheiro al-Karaji (~953 a ~1029 d.C.): o Al-Badi' fi'l-hisab ("O maravilhoso livro de cálculo"), o Al-Fakhri fi'l-jabr wa'l-muqabala ("O glorioso livro de álgebra") e o Al-Kafi fi'l-hisab ("O livro suficiente de aritmética"). Seguindo a tradição de al-Karaji, o matemático al-Samawal (~1130 a ~1180 d.C.) utiliza as frações decimais em sua obra Al-Bahir fi'l-jabr ("O brilhante livro de álgebra"). Mas foi o matemático al-Kashi (1380 a 1429 d.C.) que ganhou fama ao aplicar uma notação decimal em seus estudos; é dele o tratado Miftah al-Hisab ("A chave para a aritmética"), de 1.427, em que calcula o número π (pi) com uma precisão de nove casas sexagesimais, equivalente a dezessete casas decimais, um feito que só seria superado pelo matemático alemão Ludolph van Ceulen em 1.596, quando alcançou uma precisão de 35 casas decimais para o cálculo do π que, entretanto, não é um número racional.
 |
| Manuscrito de al-Kashi calculando o número π. |
 |
| Excerto do livro De Thiende, de Simon Stevin, onde se vê a notação adotada pelo mate-mático para os números decimais. |
$$ 3\frac{1.416}{1.000} $$
Seria decomposta em uma soma de frações de potências de dez:
$$ \frac{3}{10^{0}}+\frac{1}{10^{1}}+\frac{4}{10^{2}}+\frac{1}{10^{3}}+\frac{6}{10^{4}} $$
Ou ainda:
Ou ainda:
$$ \frac{3}{1}+\frac{1}{10}+\frac{4}{100}+\frac{1}{1.000}+\frac{6}{10.000} $$
Representados desta forma:
Em que os números dentro dos círculos indicam as potências das frações decimais associadas a cada dígito, dentro das regras do nosso sistema posicional. Outro matemático que igualmente fez uso das frações decimais e dos números decimais que os representam foi o alemão Bartholomaeus Pitiscus, quando publica em 1595 a obra Trigonometriae sive de dimensione triangulorum.
Nela, o matemático utiliza duas notações diferentes: a aplicação das frações decimais, bem como uma barra vertical separando a parte inteira da fracionária. Além destes dois últimos, muitos outros matemáticos do período renascentista testaram novas simbologias, procurando criar uma notação mais eficiente do ponto de vista operacional e mais simples, em termos semióticos, que aquela fornecida pelas frações para a representação de números não inteiros, demonstrando que a notação matemática teve um avanço explosivo e desordenado nessa época, antes de atingir uma uniformidade e ampla aceitação na comunidade matemática. A representação de números decimais derivados de frações acabou por receber o nome de números racionais, pois simbolizam o resultado de uma razão, ou quociente, entre dois números inteiros. Bom, uma fração é chamada própria quando o número racional que a representa é menor que a unidade, que o todo. São próprias todas as frações cujo numerador é menor que o denominador. A fração será imprópria no caso oposto, pois o número racional que a representa é maior que a unidade, que o todo, contrário ao conceito original de fração: a representação numérica de uma parte da unidade, do 'todo' mensurado. Sendo assim, considere a fração imprópria abaixo:
Representados desta forma:
Em que os números dentro dos círculos indicam as potências das frações decimais associadas a cada dígito, dentro das regras do nosso sistema posicional. Outro matemático que igualmente fez uso das frações decimais e dos números decimais que os representam foi o alemão Bartholomaeus Pitiscus, quando publica em 1595 a obra Trigonometriae sive de dimensione triangulorum.
 |
| Uso da barra vertical (seta verde e laranja) e das frações decimais (seta azul e laranja) por Bartholomaeus Pitiscus para representar um número não inteiro. |
$$ \frac{37}{16} $$
Vejamos então como fica o processo da divisão para inclusão da parte fracionária ou décimos, nas palavras de Stevin:
Até aqui, sem novidades: o dividendo 37, dividido por 16, resulta 2, que multiplicado por 16 dá 32. Trinta e sete subtraído de trinta e dois fornece 5 como resto. A partir deste ponto, entra o conceito de Stevin: cada décimo, ou casa decimal, corresponde à soma de uma fração cujo denominador é uma potência crescente de dez, ou seja:
Vejamos então como fica o processo da divisão para inclusão da parte fracionária ou décimos, nas palavras de Stevin:
Até aqui, sem novidades: o dividendo 37, dividido por 16, resulta 2, que multiplicado por 16 dá 32. Trinta e sete subtraído de trinta e dois fornece 5 como resto. A partir deste ponto, entra o conceito de Stevin: cada décimo, ou casa decimal, corresponde à soma de uma fração cujo denominador é uma potência crescente de dez, ou seja:
$$ \frac{2}{10^{0}}+\frac{\blacksquare }{10^{1}}+\frac{\blacksquare }{10^{2}}+\frac{\blacksquare }{10^{3}}+\frac{\blacksquare }{10^{4}}+... $$
Como 100 é igual a 1, a primeira fração representa a parte inteira do número racional, pois que 2/1 é 2; as demais frações representarão os décimos, sendo que cada numerador (simbolizado por uma pequena cartela preta) conterá um número oriundo das sucessivas divisões do resto. Assim, para prosseguir com essa divisão, o resto será multiplicado por 10 a cada casa decimal de precisão que se quiser obter a mais para o número racional resultante. Desse modo:
Neste processo, o quociente passará a indicar a parte fracionária, daí porque a inclusão da vírgula. Então, tendo multiplicado o resto 5 por 10, gerando 50, podemos retomar o processo da divisão. Seguindo a moda egípcia, pergunta-se: que número multiplicado por 16 resulta 50? A resposta é 3, pois 16 × 3 = 48, que é o valor que, não sendo igual, mais se aproxima de 50. Temos:
Então, no lugar da primeira cartela preta da parte fracionária, de acordo com o modelo de Stevin, entrará o 3, primeiro décimo do número racional:
Como 100 é igual a 1, a primeira fração representa a parte inteira do número racional, pois que 2/1 é 2; as demais frações representarão os décimos, sendo que cada numerador (simbolizado por uma pequena cartela preta) conterá um número oriundo das sucessivas divisões do resto. Assim, para prosseguir com essa divisão, o resto será multiplicado por 10 a cada casa decimal de precisão que se quiser obter a mais para o número racional resultante. Desse modo:
Neste processo, o quociente passará a indicar a parte fracionária, daí porque a inclusão da vírgula. Então, tendo multiplicado o resto 5 por 10, gerando 50, podemos retomar o processo da divisão. Seguindo a moda egípcia, pergunta-se: que número multiplicado por 16 resulta 50? A resposta é 3, pois 16 × 3 = 48, que é o valor que, não sendo igual, mais se aproxima de 50. Temos:
Então, no lugar da primeira cartela preta da parte fracionária, de acordo com o modelo de Stevin, entrará o 3, primeiro décimo do número racional:
$$ \frac{2}{10^{0}}+\frac{3}{10^{1}}+\frac{\blacksquare }{10^{2}}+\frac{\blacksquare }{10^{3}}+\frac{\blacksquare }{10^{4}}+... $$
O novo resto, 2, multiplicado por 10, constitui a segunda parcela fracionária, ou seja, o segundo décimo. O valor 20 pode ser dividido por 16. Imitando os egípcios, perguntamos: que número multiplicado por 16 resulta 20? O valor que mais se aproxima de 20 é 16, pois que 16 × 1 = 16. Assim:
Agora, no lugar da segunda cartela preta da parte fracionária, conforme o modelo de Stevin, entrará o 1, segundo décimo do número racional:
O novo resto, 2, multiplicado por 10, constitui a segunda parcela fracionária, ou seja, o segundo décimo. O valor 20 pode ser dividido por 16. Imitando os egípcios, perguntamos: que número multiplicado por 16 resulta 20? O valor que mais se aproxima de 20 é 16, pois que 16 × 1 = 16. Assim:
Agora, no lugar da segunda cartela preta da parte fracionária, conforme o modelo de Stevin, entrará o 1, segundo décimo do número racional:
$$ \frac{2}{10^{0}}+\frac{3}{10^{1}}+\frac{1}{10^{2}}+\frac{\blacksquare }{10^{3}}+\frac{\blacksquare }{10^{4}}+... $$
O novo resto deste processo de divisão, 4, uma vez multiplicado por 10, constitui a terceira parcela fracionária, ou seja, o terceiro décimo. O valor 40 pode ser dividido por 16. Seguindo os passos dos egípcios, perguntamos: que número multiplicado por 16 resulta 40? O valor que mais se aproxima de 40 é 32, pois que 16 × 2 = 32. Assim:
Agora, no lugar da terceira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 2, terceiro décimo do número racional:
O novo resto deste processo de divisão, 4, uma vez multiplicado por 10, constitui a terceira parcela fracionária, ou seja, o terceiro décimo. O valor 40 pode ser dividido por 16. Seguindo os passos dos egípcios, perguntamos: que número multiplicado por 16 resulta 40? O valor que mais se aproxima de 40 é 32, pois que 16 × 2 = 32. Assim:
Agora, no lugar da terceira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 2, terceiro décimo do número racional:
$$ \frac{2}{10^{0}}+\frac{3}{10^{1}}+\frac{1}{10^{2}}+\frac{2}{10^{3}}+\frac{\blacksquare }{10^{4}}+... $$
O novo resto deste processo de divisão, 8, uma vez multiplicado por 10, constitui a quarta parcela fracionária, ou seja, o quarto décimo. Fazendo um último apelo aos egípcios, perguntamos: que número multiplicado por 16 resulta 80? O valor exato é 5, pois que 16 × 5 = 80. Assim:
Agora, no lugar da quarta cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 5, quarto décimo do número racional:
O novo resto deste processo de divisão, 8, uma vez multiplicado por 10, constitui a quarta parcela fracionária, ou seja, o quarto décimo. Fazendo um último apelo aos egípcios, perguntamos: que número multiplicado por 16 resulta 80? O valor exato é 5, pois que 16 × 5 = 80. Assim:
Agora, no lugar da quarta cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 5, quarto décimo do número racional:
$$ \frac{2}{10^{0}}+\frac{3}{10^{1}}+\frac{1}{10^{2}}+\frac{2}{10^{3}}+\frac{5}{10^{4}} $$
Ou ainda, segundo a nomenclatura de Stevin:
A divisão de 37 por 16 resultou no número racional 2,3125 em notação moderna; na parte fracionária o número 3 representa os décimos; o número 1 representa os centésimos; o número 2, os milésimos e o número 5, os décimos de milésimo. Porém, existem números racionais cuja parte fracionária estende-se ao infinito, recebendo por isso o nome de dízimas periódicas. Vejamos um exemplo de dízima com a obtenção do número racional equivalente à fração 1/3:
O que acontece nesta divisão é simples: sendo o 1 menor que o 3, a divisão não ocorre; sendo assim, o quociente é zero, que multiplicado por 3 resulta zero; 1 subtraído de zero resta 1. A partir deste ponto, retomamos o processo de cálculo dos décimos: para cada casa decimal calculada na parte fracionária do número racional, o resto é multiplicado por 10, o que equivale a dividir por uma potência crescente de base dez. Assim:
À esquerda do quociente, incluímos uma vírgula para iniciar o cálculo da parte fracionária e, ao mesmo tempo, multiplicamos o resto 1 por 10. Agora, o resto é divisível pelo divisor 3:
Segue-se a tradicional pergunta egípcia: que número multiplicado pelo divisor 3 resulta 10? A resposta é 3, pois 3 × 3 = 9. Dez subtraído de 9 resta 1.
Para aumentarmos a precisão do número em uma casa decimal, repetimos o processo: multiplicamos o resto 1 por 10. À pergunta: "que número multiplicado pelo divisor 3 resultará 10?", novamente a resposta é 3. Note que este padrão se repete, uma vez que o cálculo do produto da casa decimal em questão, multiplicado pelo divisor 3, será sempre 9; 10 subtraído de 9 fornece, sempre, resto 1 e este processo segue indefinidamente, daí que porque o quociente é um número racional com dízima periódica: 0,33333... Considere agora a soma:
Ou ainda, segundo a nomenclatura de Stevin:
A divisão de 37 por 16 resultou no número racional 2,3125 em notação moderna; na parte fracionária o número 3 representa os décimos; o número 1 representa os centésimos; o número 2, os milésimos e o número 5, os décimos de milésimo. Porém, existem números racionais cuja parte fracionária estende-se ao infinito, recebendo por isso o nome de dízimas periódicas. Vejamos um exemplo de dízima com a obtenção do número racional equivalente à fração 1/3:
O que acontece nesta divisão é simples: sendo o 1 menor que o 3, a divisão não ocorre; sendo assim, o quociente é zero, que multiplicado por 3 resulta zero; 1 subtraído de zero resta 1. A partir deste ponto, retomamos o processo de cálculo dos décimos: para cada casa decimal calculada na parte fracionária do número racional, o resto é multiplicado por 10, o que equivale a dividir por uma potência crescente de base dez. Assim:
À esquerda do quociente, incluímos uma vírgula para iniciar o cálculo da parte fracionária e, ao mesmo tempo, multiplicamos o resto 1 por 10. Agora, o resto é divisível pelo divisor 3:
Segue-se a tradicional pergunta egípcia: que número multiplicado pelo divisor 3 resulta 10? A resposta é 3, pois 3 × 3 = 9. Dez subtraído de 9 resta 1.
Para aumentarmos a precisão do número em uma casa decimal, repetimos o processo: multiplicamos o resto 1 por 10. À pergunta: "que número multiplicado pelo divisor 3 resultará 10?", novamente a resposta é 3. Note que este padrão se repete, uma vez que o cálculo do produto da casa decimal em questão, multiplicado pelo divisor 3, será sempre 9; 10 subtraído de 9 fornece, sempre, resto 1 e este processo segue indefinidamente, daí que porque o quociente é um número racional com dízima periódica: 0,33333... Considere agora a soma:
$$ 2\frac{25}{37}+\frac{5}{16} $$
Neste exemplo, temos que transformar a fração mista em uma fração imprópria; neste caso, para obtermos o numerador, multiplicamos o 2 por 37 e o resultado será somado a 25:
Neste exemplo, temos que transformar a fração mista em uma fração imprópria; neste caso, para obtermos o numerador, multiplicamos o 2 por 37 e o resultado será somado a 25:
$$ 2\times 37=74\rightarrow 74+25=99 $$
O denominador permanece o mesmo, ou seja, 37. Teremos:
O denominador permanece o mesmo, ou seja, 37. Teremos:
$$ \frac{99}{37}+\frac{5}{16} $$
Agora, obtemos o mínimo múltiplo comum entre os denominadores 37 e 16, que resulta: 592. Prosseguindo com o cálculo:
Agora, obtemos o mínimo múltiplo comum entre os denominadores 37 e 16, que resulta: 592. Prosseguindo com o cálculo:
$$ \frac{1.584+185}{592}=\frac{1.769}{592} $$
Temos a fração 1769/592 como resultado; se quisermos saber o valor decimal dessa fração, precisamos proceder à divisão longa, como demonstrada neste capítulo, que fornecerá como resposta: 2,988175... Se, ao invés disso, tivermos no lugar da soma das frações as suas respectivas notações decimais, vem:
Temos a fração 1769/592 como resultado; se quisermos saber o valor decimal dessa fração, precisamos proceder à divisão longa, como demonstrada neste capítulo, que fornecerá como resposta: 2,988175... Se, ao invés disso, tivermos no lugar da soma das frações as suas respectivas notações decimais, vem:
$$ 2,675675...+0,3125 $$
A soma com notação decimal é mais simples que soma de frações; basta alinharmos os algarismos de ambos os números, cada qual em sua posição decimal, dentro das regras do sistema posicional; na parte inteira: unidade com unidade, dezena com dezena, centena com centena, etc. E na parte fracionária posicionamos décimo com décimo, centésimo com centésimo, milésimo com milésimo e assim sucessivamente. De acordo com essa regra, temos:
Depois, basta somarmos os números conforme a casa decimal que ocupem, seguindo a convenção moderna, ou seja, da direita para a esquerda; entretanto, também podemos somar da esquerda para a direita, seguindo a convenção adotada pelos antigos hindus, como demonstrado no primeiro volume desta série. Sendo assim, para os números posicionados nas casas decimais mais à direita, no número racional verde, que não tem com quem serem somados, seus valores são mantidos inalterados:
Somando agora os números que ocupam os décimos de milésimos (o 6 e o 5), vem:
Já sabemos que dois números não podem ocupar uma mesma posição em nosso sistema numérico, o que implica dizer que o 1 das dezenas no número 11 da resposta deve deslocar-se uma casa decimal à esquerda (a dos milésimos), sendo somado ao 5 e ao 2, que já ocupam essa mesma casa, resultando:
Agora, somamos os números que ocupam a casa dos centésimos, ou seja, o 7 e o 1, resultando:
Seguindo o procedimento indicado, somaremos agora os números que ocupam a casa dos décimos, a saber, o 6 e o 3:
Finalizamos a adição somando os números que ocupam a casa das unidades, quais sejam, o 0 e o 2:
Pronto! A soma está completa, resultando no número racional: 2,988175... Quando se conhece e se aplica corretamente as regras do sistema posicional hindu-arábico no sistema decimal, a adição se torna uma operação aritmética muito simples entre dois ou mais números racionais. Pois bem, considere agora a seguinte subtração entre duas frações próprias:
A soma com notação decimal é mais simples que soma de frações; basta alinharmos os algarismos de ambos os números, cada qual em sua posição decimal, dentro das regras do sistema posicional; na parte inteira: unidade com unidade, dezena com dezena, centena com centena, etc. E na parte fracionária posicionamos décimo com décimo, centésimo com centésimo, milésimo com milésimo e assim sucessivamente. De acordo com essa regra, temos:
Depois, basta somarmos os números conforme a casa decimal que ocupem, seguindo a convenção moderna, ou seja, da direita para a esquerda; entretanto, também podemos somar da esquerda para a direita, seguindo a convenção adotada pelos antigos hindus, como demonstrado no primeiro volume desta série. Sendo assim, para os números posicionados nas casas decimais mais à direita, no número racional verde, que não tem com quem serem somados, seus valores são mantidos inalterados:
Somando agora os números que ocupam os décimos de milésimos (o 6 e o 5), vem:
Já sabemos que dois números não podem ocupar uma mesma posição em nosso sistema numérico, o que implica dizer que o 1 das dezenas no número 11 da resposta deve deslocar-se uma casa decimal à esquerda (a dos milésimos), sendo somado ao 5 e ao 2, que já ocupam essa mesma casa, resultando:
Agora, somamos os números que ocupam a casa dos centésimos, ou seja, o 7 e o 1, resultando:
Seguindo o procedimento indicado, somaremos agora os números que ocupam a casa dos décimos, a saber, o 6 e o 3:
Finalizamos a adição somando os números que ocupam a casa das unidades, quais sejam, o 0 e o 2:
Pronto! A soma está completa, resultando no número racional: 2,988175... Quando se conhece e se aplica corretamente as regras do sistema posicional hindu-arábico no sistema decimal, a adição se torna uma operação aritmética muito simples entre dois ou mais números racionais. Pois bem, considere agora a seguinte subtração entre duas frações próprias:
$$ \frac{35}{43}-\frac{7}{11} $$
A divisão longa de cada uma das frações nos fornece seus respectivos números decimais:
A divisão longa de cada uma das frações nos fornece seus respectivos números decimais:
$$ 0,813953...-0,636363... $$
Obedecendo ao alinhamento dos algarismos de ambos os números, cada qual em sua casa decimal, dentro das regras do sistema posicional, proporcionada pelo sistema numérico hindu-arábico, temos:
Seguindo a convenção moderna, subtraímos cada uma das casas decimais da direita para a esquerda (mas também poderia ser da esquerda para a direita, se seguíssemos a convenção hindu); assim, nesta primeira etapa obtemos:
Na primeira coluna à direita com números, correspondente à casa dos milésimos de milésimo, subtraiu-se 3 de 3, restando 0. Agora, na casa correspondente aos centésimos de milésimo, temos de subtrair 6 de 5, o que não é possível já que 5 é menor que 6. Veja que interessante: ainda que estejamos calculando a diferença entre dois números racionais, a subtração efetuada em cada casa decimal segue a regra dos números inteiros: a de que não é possível subtrair um número maior de outro menor. Para esses casos aplica-se a técnica aprendida na escola e denominada "empresta-um". Para entender esta técnica, é preciso lembrar que cada casa decimal à esquerda daquela em que estamos calculando é uma ordem de grandeza, ou dez vezes maior. Então, pegar emprestado da casa decimal à esquerda significa pegar uma dezena emprestada. Para o presente caso, pegamos uma dezena da casa dos décimos de milésimo, onde temos o número 9; com essa dezena emprestada, restam 8 dezenas na casa dos décimos de milésimo e a casa dos centésimos de milésimo, que tinha 5 unidades, ficará com 15 unidades. A subtração agora é possível, pois 15 é maior que 6. Temos:
Obedecendo ao alinhamento dos algarismos de ambos os números, cada qual em sua casa decimal, dentro das regras do sistema posicional, proporcionada pelo sistema numérico hindu-arábico, temos:
Seguindo a convenção moderna, subtraímos cada uma das casas decimais da direita para a esquerda (mas também poderia ser da esquerda para a direita, se seguíssemos a convenção hindu); assim, nesta primeira etapa obtemos:
Na primeira coluna à direita com números, correspondente à casa dos milésimos de milésimo, subtraiu-se 3 de 3, restando 0. Agora, na casa correspondente aos centésimos de milésimo, temos de subtrair 6 de 5, o que não é possível já que 5 é menor que 6. Veja que interessante: ainda que estejamos calculando a diferença entre dois números racionais, a subtração efetuada em cada casa decimal segue a regra dos números inteiros: a de que não é possível subtrair um número maior de outro menor. Para esses casos aplica-se a técnica aprendida na escola e denominada "empresta-um". Para entender esta técnica, é preciso lembrar que cada casa decimal à esquerda daquela em que estamos calculando é uma ordem de grandeza, ou dez vezes maior. Então, pegar emprestado da casa decimal à esquerda significa pegar uma dezena emprestada. Para o presente caso, pegamos uma dezena da casa dos décimos de milésimo, onde temos o número 9; com essa dezena emprestada, restam 8 dezenas na casa dos décimos de milésimo e a casa dos centésimos de milésimo, que tinha 5 unidades, ficará com 15 unidades. A subtração agora é possível, pois 15 é maior que 6. Temos:
A técnica do "empresta-um" é a única situação em que é permitido ter dois algarismos na mesma casa decimal. O procedimento adotado é apenas um artifício que torna possível a subtração do minuendo (15) pelo subtraendo (6); o resultado da subtração (obtido nas cartelas vermelhas), que é a resposta que nos interessa, terá um único número por casa decimal. Calculando agora na casa dos décimos de milésimo, subtraímos 3 de 8, restando 5:
Dando continuidade ao cálculo, passamos à casa dos milésimos, onde subtrairemos 6 de 3: novamente, esta subtração não é possível, pois 3 é menor que 6. Então recorremos à técnica do "empresta-um", pegando uma dezena emprestada da casa decimal acima, a dos centésimos, e somando essa dezena ao 3, resultando 13. Como uma dezena foi retirada da casa dos centésimos (e só havia uma dezena), essa casa fica zerada. Porém, a subtração de 13 por 6 agora é possível:
Prosseguindo, calcularemos agora a subtração na casa dos centésimos; como não dá para subtrair 3 de 0, pegamos emprestado uma dezena da casa dos décimos. Como há 8 dezenas nessa casa, ela fica agora com 7 dezenas e a casa dos centésimos, que estava vazia, fica agora com 10, tornando possível a subtração por 3:
A seguir, calculamos a subtração na casa dos décimos, que não apresenta maiores problemas, pois 7 é maior que 6:
Finalmente, calculamos a subtração na casa das unidades. Seguindo os preceitos do matemático hindu Brahmagupta, quando afirma que: "Zero subtraído de zero é zero", teremos:
O procedimento adotado não se altera, de modo que o primeiro movimento desta 'dança dos números' se mantém. Veja:
O segundo movimento também não tem alterações: é preciso obter uma dezena de empréstimo a ser somada ao 5, que se encontra na casa dos centésimos de milésimo. O problema é que não há dezenas nas três casas decimais acima; apenas na casa dos décimos é que há 8 dezenas disponíveis. Como não há alternativa a não ser obter esse empréstimo, a transferência de dezenas deve ocorrer de uma casa decimal para as inferiores, um passo de cada vez. Sendo assim, pega-se uma dezena dos décimos, que fica com 7 dezenas; e a casa decimal inferior, a dos centésimos, passa a ter uma dezena disponível:
Repete-se o processo, agora pegando uma dezena emprestada da casa dos centésimos (que ficará com 9 dezenas) para a dos milésimos, que passa a ter uma dezena para si:
Continuamos repetindo este processo, pegando agora uma dezena emprestada da casa dos milésimos (que fica com 9 dezenas) e passando à dos décimos de milésimo (que adquire uma dezena para si):
Repetimos mais uma vez este processo, pegando agora uma dezena emprestada da casa dos décimos de milésimo (que fica com 9 dezenas) e passando à dos centésimos de milésimo (que adquire uma dezena para si, somada às 5 unidades que já existiam nessa casa decimal):
Agora é possível subtrair 15 de 6, restando 9. Deslocando uma casa decimal à esquerda, subtraímos 3 de 9, restando 6. Deslocando outra casa decimal à esquerda, subtraímos 6 de 9, restando 3. Deslocando-se mais uma casa decimal à esquerda, subtraímos 3 de 9, restando 6. Chegando à casa dos décimos, sub-traímos 6 de 7, restando 1. E por fim, na casa das unidades, subtraímos 0 de 0, restando 0:
Quando se aprende os passos dessa valsa dos números, com seus empréstimos e trocas de posições conforme a casa decimal em que se operam as contas, o cálculo entre números decimais soa como um baile matemático!
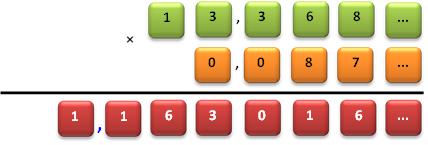
Considere agora a multiplicação entre as duas frações abaixo:
$$ 13\frac{7}{19}\times \frac{2}{23} $$
Os números racionais equivalentes a essas duas frações são:
Os números racionais equivalentes a essas duas frações são:
$$ 13,368...\times 0,087... $$
Em seguida, adota-se o mesmo procedimento da soma e da subtração quanto ao posicionamento dos dois números, alinhando os dígitos conforme sua escala de grandeza; assim:
Na casa das dezenas temos apenas o número 1; na casa das unidades temos os números 3 e 0; na casa dos décimos também temos os números 3 e 0; na casa dos centésimos temos os números 6 e 8; finalmente, na casa dos milésimos alinham-se os números 8 e 7. Na multiplicação, cada casa decimal do multiplicador (ou seja, o 0,087...) é multiplicada por cada uma das casas decimais do multiplicando (que é o 13,368...), resultando num produto cartesiano, bem sintetizado pela famosa frase dos três mosqueteiros: "Um por todos e todos por um!".
Começando pelo 7, a menor casa decimal do multiplicador, faremos a multiplicação dele com cada número do multiplicando:
Em seguida, adota-se o mesmo procedimento da soma e da subtração quanto ao posicionamento dos dois números, alinhando os dígitos conforme sua escala de grandeza; assim:
Na casa das dezenas temos apenas o número 1; na casa das unidades temos os números 3 e 0; na casa dos décimos também temos os números 3 e 0; na casa dos centésimos temos os números 6 e 8; finalmente, na casa dos milésimos alinham-se os números 8 e 7. Na multiplicação, cada casa decimal do multiplicador (ou seja, o 0,087...) é multiplicada por cada uma das casas decimais do multiplicando (que é o 13,368...), resultando num produto cartesiano, bem sintetizado pela famosa frase dos três mosqueteiros: "Um por todos e todos por um!".
Começando pelo 7, a menor casa decimal do multiplicador, faremos a multiplicação dele com cada número do multiplicando:
Começando a multiplicação com o número 8 na casa dos milésimos, como indicado, resultam 56. Como não é possível ter dois números numa mesma casa decimal, o número 5 (que é uma dezena maior) passa para a casa dos centésimos:
Em seguida, o 7 multiplica o 6 da casa dos centésimos, resultando 42, somado à dezena anterior (5, em azul), dá 47. Como não é possível ter dois números numa mesma casa decimal, o 4 (que é uma dezena maior) passa para a casa dos décimos:
Prosseguindo, multiplicamos agora o 7 pelo 3 da casa dos décimos, resultando 21 que, somado à dezena anterior (4, em azul), dá 25. Mais uma vez, não é possível ter dois números na mesma casa decimal, de modo que o 2, ou seja, as duas dezenas do resultado, passam para a casa das unidades:
Agora, multiplicamos o 7 pelo 3 da casa das unidades, resultando 21 que, somado às duas dezenas anteriores (2, em azul), dá 23. Já sabemos que dois números não ocupam uma mesma casa decimal, de sorte que o 3 fica na casa das unidades e o 2 pula para a casa das dezenas:
Finalmente, multiplicamos o 7 pelo 1 da casa das dezenas, resultando 7 que, somado às duas dezenas anteriores (2, em azul), resulta 9:
Bom, multiplicamos o 7 (a menor dezena do multiplicador) por todas as dezenas do multiplicando. O mesmo processo será aplicado para a próxima dezena do multiplicador, o 8 (que ocupa a casa dos centésimos). O resultado obtido será:
Observe as operações realizadas:
- O resultado da multiplicação começa na casa do multiplicador; neste caso, começa na casa dos centésimos, onde se encontra o 8;
- 8 multiplicado por 8 dá 64; o 4 fica na casa dos centésimos e o 6, que é uma dezena maior, vai para a casa dos décimos (em azul);
- 8 multiplicado por 6 dá 48, que somados a 6 (em azul) dá 54; o 4 fica na casa dos décimos e o 5, que é uma dezena maior, vai para a casa das unidades (em azul);
- 8 multiplicado por 3 dá 24, que somados a 5 (em azul) dá 29; o 9 fica na casa das unidades e o 2, que é uma dezena maior, vai para a casa das dezenas (em azul);
- 8 multiplicado por 3 dá 24, que somados a 2 (em azul) dá 26; o 6 fica na casa das dezenas e o 2, que é uma dezena maior, vai para a casa das centenas (em azul);
- Finalmente, o 8 multiplicado por 1 dá 8, que somados a 2 (em azul) dá 10; o 0 fica na casa das centenas e o 1, que é uma dezena maior, vai par a casa dos milhares.
Agora
que já multiplicamos o 8, repetimos o mesmo processo para a próxima dezena do multiplicador, o 0 (que ocupa a casa dos
décimos). O resultado obtido será:
Observe as operações realizadas:
- O resultado da multiplicação começa na casa do multiplicador; neste caso, começa na casa dos décimos, onde se encontra o 0;
- Como qualquer número multiplicado por zero dá zero, basta posicionarmos cada resultado (que é sempre o mesmo) em sua respectiva casa decimal.
A
última etapa de multiplicação nesta conta envolve repetimos o mesmo processo
para a próxima dezena do multiplicador,
outro 0 (que ocupa a casa das unidades).
O resultado obtido será:
Observe as operações realizadas:
- O resultado da multiplicação começa na casa do multiplicador; neste caso, começa na casa das unidades, onde se encontra o 0;
- Novamente, como qualquer número multiplicado por zero dá zero, basta posicionarmos cada resultado (que é sempre o mesmo) em sua respectiva casa decimal.
Agora que todos os algarismos do multiplicador foram multiplicados por todos os algarismos do multiplicando, basta somarmos os resultados parciais para cada casa decimal:
Somando os resultados parciais da direita para a esquerda, temos:
Observe o resultado:
- As reticências representam apenas que o número é uma dízima, mas não contém nenhum dígito ou algarismo significativo; logo, não fazemos contas com ele, mas indica-se que o número resultante também é uma dízima.
- O algarismo 6 não tem ninguém com quem ser somado, de modo que nessa casa decimal o resultado é ele mesmo;
- Somando 7 com 4 dá 11; o algarismo 1 das unidades fica nessa casa decimal e o outro 1, que é uma dezena maior, vai para a próxima casa decimal, à esquerda;
- Esse número 1 somado a 5, 4 e zero dá 10; o algarismo 0 das unidades fica nessa casa decimal e o 1, que é uma dezena maior, vai para a próxima casa decimal, à esquerda;
- O algarismo 1 somado a 3, 9, 0 e 0 dá 13; o algarismo 3 das unidades fica nessa casa decimal e o outro 1, que é uma dezena maior, vai para a próxima casa decimal, à esquerda;
- O algarismo 1 somado a 9, 6, 0 e 0 dá 16; o algarismo 6 das unidades fica nessa casa decimal e o outro 1, que é uma dezena maior, vai para a próxima casa decimal, à esquerda;
- O algarismo 1 somado a 0, 0 e 0 dá 1; como o resultado é uma unidade, não há deslocamento entre casas decimais;
- Na casa decimal à esquerda da última soma temos os algarismos 1, 0 e zero, que somados dá 1;
- Finalmente, O algarismo 0 não tem ninguém com quem ser somado, de modo que nessa casa decimal o resultado é ele mesmo;
Para
finalizar essa multiplicação entre dois números decimais é preciso saber onde
posicionar a vírgula do número resultante, que também é um número decimal. Para
isso, observe o multiplicador e o multiplicando:
Para posicionar a vírgula no número decimal
resultante da multiplicação, basta contar a quantidade de casas decimais após a
vírgula tanto do multiplicador quanto
do multiplicando (descartamos as
casas decimais com reticências). Temos um total de 6 casas decimais (3 de cada
número); então, contando as casas decimais significativas do resultado, da
direita para a esquerda (excluindo-se as reticências), a vírgula ficará
posicionada conforme abaixo (em azul):
Observe: antes da vírgula tínhamos uma casa
decimal à esquerda do 1 com o algarismo 0, que não tem valor significativo em
nosso sistema decimal (ao contrário do zero entre os números 3 e 1, que indica
ausência de valor na casa decimal que ocupa). Assim, a multiplicação entre
13,368... e 0,087... fornece como resultado o número decimal 1,163016... Como
último caso, vamos estudar agora a divisão entre as duas frações abaixo:
$$ 12\frac{37}{144}\div \frac{23}{43} $$
Os números racionais equivalentes a essas duas frações são:
Os números racionais equivalentes a essas duas frações são:
$$ 12,256...\div 0,534... $$
A estratégia neste caso é transformar ambos os números decimais em números 'inteiros', tomando como referência o número com maior quantidade de casas decimais significativas, que neste caso é o dividendo (12,256...). Desprezando as casas decimais representadas por reticências, para que este número se torne um 'inteiro' ele deve ser multiplicado por 1.000:
A estratégia neste caso é transformar ambos os números decimais em números 'inteiros', tomando como referência o número com maior quantidade de casas decimais significativas, que neste caso é o dividendo (12,256...). Desprezando as casas decimais representadas por reticências, para que este número se torne um 'inteiro' ele deve ser multiplicado por 1.000:
$$ 12,256\times 1.000=12.256 $$
Se multiplicamos 12,256 por 1.000, então, para manter a divisão entre 12,256 e 0,534 inalterada, deveremos multiplicar 0,534 também por 1.000, obtendo:
Se multiplicamos 12,256 por 1.000, então, para manter a divisão entre 12,256 e 0,534 inalterada, deveremos multiplicar 0,534 também por 1.000, obtendo:
$$ 0,534\times 1.000=534 $$
Logo, a divisão fica com esta nova aparência:
Logo, a divisão fica com esta nova aparência:
$$ 12.256\div 534 $$
Importante observar que fizemos uma simplificação ao desprezar as casas decimais representadas por reticências tanto no dividendo quanto no divisor. Esta simplificação resultará em um erro de aproximação na divisão entre os dois números 'inteiros', pois ambos são simplificações para os números racionais originais, que possuem um número infinito de casas decimais (uma vez que as frações não resultam exatas). Dito isto, a divisão destes números 'inteiros' já não apresenta segredos:
Importante observar que fizemos uma simplificação ao desprezar as casas decimais representadas por reticências tanto no dividendo quanto no divisor. Esta simplificação resultará em um erro de aproximação na divisão entre os dois números 'inteiros', pois ambos são simplificações para os números racionais originais, que possuem um número infinito de casas decimais (uma vez que as frações não resultam exatas). Dito isto, a divisão destes números 'inteiros' já não apresenta segredos:
Tomamos os algarismos do dividendo 12.256 da esquerda para a direita até que o valor obtido seja maior que o divisor 534: o 'dividendo' resultante será 1.225, que ao ser dividido por 534 dá 2. Multiplicando 2 por 534 obtemos 1.068. Subtrair 1.068 de 1.225 fornece 157 como resto. Do dividendo original sobrou o algarismo 6, que comporá com o resto 157 um novo número: 1.576.
Dividir 1.576 por 534 resulta 2. Multiplicando 2 por 534 obtém-se 1.068, que subtraído de 1.576 fornece 508 como resto:
A partir deste ponto, entramos no conceito de Stevin: cada décimo, ou casa decimal, corresponde à soma de uma fração cujo denominador é uma potência crescente de dez, ou seja:
$$ \frac{22}{10^{0}}+\frac{\blacksquare }{10^{1}}+\frac{\blacksquare }{10^{2}}+\frac{\blacksquare }{10^{3}}+... $$
Como 100 é igual a 1, a primeira fração representa a parte inteira do número racional, pois que 22/1 é 22; as demais frações representarão os décimos, sendo que cada numerador (simbolizado por uma pequena cartela preta) conterá um número oriundo das sucessivas divisões do resto. Assim, para prosseguir com essa divisão, o resto será multiplicado por 10 a cada casa decimal de precisão que se quiser obter a mais para o número racional resultante. Desse modo:
Neste processo, o quociente passará a indicar a parte fracionária, daí porque a inclusão da vírgula. Então, tendo multiplicado o resto 508 por 10, gerando 5.080. O novo resto, multiplicado por 10, constituirá a primeira parcela fracionária, ou seja, o primeiro décimo. O valor resultante será dividido por 534. Imitando os egípcios, perguntamos: que número multiplicado por 534 resulta 5.080? O valor que mais se aproxima de 5.080 sem ultrapassá-lo é 4.806, pois que 534 × 9 = 4.806. Assim:
Agora, no lugar da primeira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 9, primeiro décimo do número racional:
Como 100 é igual a 1, a primeira fração representa a parte inteira do número racional, pois que 22/1 é 22; as demais frações representarão os décimos, sendo que cada numerador (simbolizado por uma pequena cartela preta) conterá um número oriundo das sucessivas divisões do resto. Assim, para prosseguir com essa divisão, o resto será multiplicado por 10 a cada casa decimal de precisão que se quiser obter a mais para o número racional resultante. Desse modo:
Neste processo, o quociente passará a indicar a parte fracionária, daí porque a inclusão da vírgula. Então, tendo multiplicado o resto 508 por 10, gerando 5.080. O novo resto, multiplicado por 10, constituirá a primeira parcela fracionária, ou seja, o primeiro décimo. O valor resultante será dividido por 534. Imitando os egípcios, perguntamos: que número multiplicado por 534 resulta 5.080? O valor que mais se aproxima de 5.080 sem ultrapassá-lo é 4.806, pois que 534 × 9 = 4.806. Assim:
Agora, no lugar da primeira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 9, primeiro décimo do número racional:
$$ \frac{22}{10^{0}}+\frac{9}{10^{1}}+\frac{\blacksquare }{10^{2}}+\frac{\blacksquare }{10^{3}}+... $$
O novo resto deste processo de divisão, 274, uma vez multiplicado por 10, constitui a segunda parcela fracionária, ou seja, o segundo décimo. O valor 2.740 será dividido por 534. Seguindo os passos dos egípcios, perguntamos: que número multiplicado por 534 resulta 2.740? O valor que mais se aproxima de 2.740 é 2.670, pois que 534 × 5 = 2.670. Assim:
Agora, no lugar da segunda cartela preta da parte fracionária, de acordo com o modelo de Stevin, entrará o 5, segundo décimo do número racional:
O novo resto deste processo de divisão, 274, uma vez multiplicado por 10, constitui a segunda parcela fracionária, ou seja, o segundo décimo. O valor 2.740 será dividido por 534. Seguindo os passos dos egípcios, perguntamos: que número multiplicado por 534 resulta 2.740? O valor que mais se aproxima de 2.740 é 2.670, pois que 534 × 5 = 2.670. Assim:
Agora, no lugar da segunda cartela preta da parte fracionária, de acordo com o modelo de Stevin, entrará o 5, segundo décimo do número racional:
$$ \frac{22}{10^{0}}+\frac{9}{10^{1}}+\frac{5}{10^{2}}+\frac{\blacksquare }{10^{3}}+... $$
O novo resto deste processo de divisão, 70, uma vez multiplicado por 10 (700), constitui a terceira parcela fracionária, ou seja, o terceiro décimo. Fazendo um último apelo aos egípcios, perguntamos: que número multiplicado por 534 resulta 700? O valor que mais se aproxima de 700 sem ultrapassá-lo é 534, pois que 534 × 1 = 534. Assim:
Agora, no lugar da terceira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 1, terceiro décimo do número racional:
O novo resto deste processo de divisão, 70, uma vez multiplicado por 10 (700), constitui a terceira parcela fracionária, ou seja, o terceiro décimo. Fazendo um último apelo aos egípcios, perguntamos: que número multiplicado por 534 resulta 700? O valor que mais se aproxima de 700 sem ultrapassá-lo é 534, pois que 534 × 1 = 534. Assim:
Agora, no lugar da terceira cartela preta da parte fracionária, segundo o modelo de Stevin, entrará o 1, terceiro décimo do número racional:
$$ \frac{22}{10^{0}}+\frac{9}{10^{1}}+\frac{5}{10^{2}}+\frac{1}{10^{3}}+... $$
Ou ainda, segundo a nomenclatura de Stevin:
Portanto, a divisão:
Ou ainda, segundo a nomenclatura de Stevin:
Portanto, a divisão:
$$ 12.256\div 534 $$
Resultou no número racional (em notação decimal): 22,951... Esta divisão pode prosseguir indefinidamente, quanto mais casas decimais quisermos acrescentar ao resultado.
A conversão de 15 imperiais no exemplo de Fibonacci resultava, em barcelonenses:
Resultou no número racional (em notação decimal): 22,951... Esta divisão pode prosseguir indefinidamente, quanto mais casas decimais quisermos acrescentar ao resultado.
A conversão de 15 imperiais no exemplo de Fibonacci resultava, em barcelonenses:
$$ 20\frac{1.189}{3.289} $$
Esta fração mista corresponderia, em notação decimal, a:
$$ 20,3587... $$
Se seguíssemos a primeira simplificação apresentada para a fração original, ou seja:
Se seguíssemos a primeira simplificação apresentada para a fração original, ou seja:
$$ 20\frac{1.100}{3.300}=20\frac{11}{33}=20\frac{1}{3} $$
Esta fração mista corresponderia, em notação decimal, a:
Esta fração mista corresponderia, em notação decimal, a:
$$ 20,3333... $$
Conversão esta que agradaria ao banqueiro, pois ele ganharia alguns centavos em relação à conversão exata (sem simplificação), o que implicaria em um prejuízo de alguns centavos para o mercador. Por outro lado, se adotássemos a outra simplificação sugerida para a fração original, qual seja:
Conversão esta que agradaria ao banqueiro, pois ele ganharia alguns centavos em relação à conversão exata (sem simplificação), o que implicaria em um prejuízo de alguns centavos para o mercador. Por outro lado, se adotássemos a outra simplificação sugerida para a fração original, qual seja:
$$ 20\frac{1.200}{3.300}=20\frac{12}{33}=20\frac{4}{11} $$
Esta outra fração mista corresponderia, em notação decimal, a:
Esta outra fração mista corresponderia, em notação decimal, a:
$$ 20,3636... $$
Esta conversão, apesar de gerar um número muito próximo ao valor obtido com a fração original, ainda assim é ligeiramente maior e, rigorosamente falando, o banqueiro sairia perdendo. A bem da verdade, nas conversões cambiais, utilizamos apenas duas casas decimais para expressar os centavos, o que implica dizer que o valor original da fração mista resultaria em:
Esta conversão, apesar de gerar um número muito próximo ao valor obtido com a fração original, ainda assim é ligeiramente maior e, rigorosamente falando, o banqueiro sairia perdendo. A bem da verdade, nas conversões cambiais, utilizamos apenas duas casas decimais para expressar os centavos, o que implica dizer que o valor original da fração mista resultaria em:
$$ 20,36 $$
A primeira simplificação (a que agradaria ao banqueiro) valeria:
A primeira simplificação (a que agradaria ao banqueiro) valeria:
$$ 20,33 $$
E a segunda simplificação resultaria em:
E a segunda simplificação resultaria em:
$$ 20,36 $$
Observe nesta segunda simplificação que, como não há prejuízo para o banqueiro, ele realizaria tranquilamente a conversão. Agora que já vimos como operar com números racionais com a notação decimal, já podemos adentrar no mundo dos números irracionais.
Observe nesta segunda simplificação que, como não há prejuízo para o banqueiro, ele realizaria tranquilamente a conversão. Agora que já vimos como operar com números racionais com a notação decimal, já podemos adentrar no mundo dos números irracionais.