A álgebra é um dos grandes ramos da matemática, junto com a geometria, a teoria dos números e a análise numérica. Na definição atual, álgebra são o estudo dos símbolos matemáticos e as regras que manipulam esses símbolos. Seu nascimento, porém, teve diversos percalços e enfrentou uma longa caminhada até alcançar a semiologia e o simbolismo tal como a conhecemos hoje e nos é ensinada nas escolas. Seguindo os passos da história, comecemos essa trajetória pelos babilônios. Para esta civilização, os problemas algébricos eram propostos e solucionados em um mesmo enunciado, com representações funcionalmente abstratas por meio de segmentos mensuráveis (como comprimento, largura ou lado do quadrado) e áreas retangulares utilizadas para tratar problemas de primeiro e segundo graus, resolvidos por meio de procedimentos de corte e projeções, como o descrito abaixo, retirado da plaqueta de argila BM13901:
1. A superfície e meu confronto eu acumulei: 45', é ele. 1, a projeção,
2. Você propõe. A metade de 1 você quebra 30' e 30' você mantém.
3. 15' para 45' você acrescenta: por 1, 1 é igual. 30' que você manteve.
4. Dentro de 1, você rasga fora: 30' o confronto.
Este truncado enunciado lida com equações quadráticas utilizando figuras geométricas; assim, o lado de um quadrado é denominado confronto, cujo valor se quer descobrir. Na primeira linha do enunciado, a soma (acúmulo) da área do quadrado com o seu lado (confronto) é igual a 45'. Como não havia uma representação para frações entre os babilônios, essa soma entre a área do quadrado com o seu lado vale efetivamente 45/60, ou simplificando: 3/4.
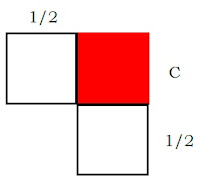
O acúmulo é uma operação simétrica de soma, ou seja, juntam-se em uma soma duas magnitudes ou seus números de medição. Entende-se como números de medição a junção de magnitudes de diferentes tipos (comprimentos e áreas – áreas e volumes – trabalhadores, tijolos e dias de trabalho), o que permite que uma área seja somada com um lado do quadrado. Afim de que essa soma tenha um significado concreto, o lado do quadrado (confronto) é fornecido como uma projeção, isto é, algo que se sobressai ou se projeta. A projeção do lado do quadrado monta um retângulo, de modo que montar significa gerar uma área. Este retângulo tem comprimento igual a 1; observe:
Na segunda linha do enunciado temos que o retângulo é quebrado ao meio, de modo que 30' é descartado e 30' é mantido. Mais uma vez, a simbologia babilônica trata de frações, de modo que 30' corresponde de fato à razão 30/60 e a divisão do comprimento do retângulo ao meio resulta em dois retângulos com comprimentos iguais a 30/60, ou simplificadamente, 1/2:
A projeção do retângulo branco (o retângulo cinza foi descartado) é rebatida no lado adjacente do quadrado:
Na terceira linha do enunciado temos o acréscimo de 15' à área 45' inicial. Este acréscimo também é uma área, resultante das projeções, pois um quadrado de lados iguais a 1/2 geram uma área igual a 1/4 (destacada em azul); e 1/4 é o mesmo que 15/60, que é a representação fracionária babilônica para 15':
A área resultante com este novo acréscimo é 1, ou seja: 15/60 + 45/60 = 60/60. Na quarta linha, afirma-se que desta área, rasga-se fora 30', que é o confronto. Rasgar tem aqui o sentido de subtrair, ou seja, subtrai-se 30' que corresponde em nossa notação à razão 30/60, ou ainda: 1/2, que é o valor do confronto ou lado do quadrado procurado, ou seja, C = 1/2.
Os demais problemas contidos nessa plaqueta de argila cozida envolvem equações do segundo grau e os resultados são sempre positivos, pois os babilônios não conheciam os números negativos. Na atualidade, o problema babilônico poderia ser enunciado da seguinte forma: a área de um quadrado, somada ao seu lado, vale 3/4. Quanto mede o lado deste quadrado? Como a área de um quadrado é a multiplicação de um lado por ele mesmo, em notação algébrica moderna teríamos:
$$ x^{2}+x=\frac{3}{4} $$
Onde x
é o tamanho do lado desse quadrado; x2
corresponde à sua área, e a soma deles é igual a 3/4. Ao somarmos a área
resultante das projeções do exemplo
babilônico, temos:
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2}=\frac{3}{4}+\left ( \frac{1}{2} \right )^{2} $$
A nova área resultante deste acréscimo será igual a 1:
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2}=\frac{3}{4}+\frac{1}{4}=\frac{3+1}{4}=\frac{4}{4}=1 $$
Por outro lado, a expressão:
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2} $$
É a forma fatorada de:
$$ \left ( x+\frac{1}{2} \right )^{2} $$
Basta lembrar que (x + 1/2)2 é o mesmo que (x + 1/2).(x + 1/2); assim, aplicando a propriedade distributiva na expressão acima, temos:
$$ \left ( x+\frac{1}{2} \right )\times\left ( x+\frac{1}{2} \right ) $$
$$ x^{2}+x\frac{1}{2}+\frac{1}{2}x+\left ( \frac{1}{2} \right )^{2} $$
$$ x^{2}+2x\frac{1}{2}+\left ( \frac{1}{2} \right )^{2} $$
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2} $$
Que é a forma não fatorada original. Isto posto, vem que:
$$ \left ( x+\frac{1}{2} \right )^{2}=1 $$
Tirando a raiz quadrada de ambos os membros da igualdade:
$$ \sqrt{\left ( x+\frac{1}{2} \right )^{2}}=\sqrt{1} $$
$$ x+\frac{1}{2}=1 $$
Rasgando 1/2 conforme a descrição babilônica, quer dizer, subtraindo 1/2 de cada lado da equação, temos:
$$ x+\frac{1}{2}-\frac{1}{2}=1-\frac{1}{2} $$
Finalmente, chegamos ao que os babilônios chamavam de confronto, ou seja, ao valor procurado do lado do quadrado:
$$ x=\frac{1}{2} $$
De fato, existem inúmeras plaquetas de argila babilônicas lidando com equações quadráticas, utilizando o mesmo algoritmo geométrico do exemplo acima, aplicado a lados e áreas de retângulos em 5 passos, como é o caso da tabuleta YBC3879 (um documento jurídico contendo equações quadráticas) produzida por volta de 2.000 a.C. e a YBC4663, produzida entre os séculos XIX e XVII a.C. e contendo problemas relativos à escavação de trincheiras.
Em notação moderna, estes problemas envolvem
geralmente a solução de um par de equações da forma:
$$ \left\{\begin{matrix}x+y=b\\ x\times y=c\end{matrix}\right. $$
Cujo desenvolvimento produz uma equação quadrática. Observe:
$$ x\times y=c\rightarrow y=\frac{c}{x} $$
Substituindo a equação acima nesta:
$$ x+y=b $$
Obtemos:
$$ x+\frac{c}{x}=b $$
$$ \frac{x^{2}+c}{x}=b $$
$$ x^{2}+c=bx $$
Finalmente, a equação quadrática fica assim:
$$ x^{2}-bx+c=0 $$
$$ \frac{b}{2}+\square =x $$
Onde a cartela branca é o pedaço que falta para que o segmento b/2 atinja o tamanho do segmento x. Mas sabemos que:
$$ \frac{b}{2}=\frac{x+y}{2} $$
Como enunciado pelo algoritmo no passo 1. Substituindo esta equação na anterior, temos:
$$ \frac{x+y}{2}+\square =x $$
$$ \square =x-\frac{x+y}{2} $$
$$ \square =\frac{2x-x-y}{2} $$
$$ \square =\frac{x-y}{2} $$
Ou seja, o segmento b/2 pode ser expresso como:
$$ \frac{b}{2}=x-\frac{x-y}{2} $$
Ou pode ser expresso como:
$$ \frac{b}{2}=y+\frac{x-y}{2} $$
O quadrado verde excede o retângulo em área na altura, como indicado pela região laranja, mas é inferior em área na largura, como apontado pela região azul. Comparando estas áreas, temos:
Note que a área laranja é maior que a área azul de uma quantia igual à área quadrada marrom. Em resumo: o quadrado verde é maior que o retângulo vermelho e azul de um valor igual à área marrom, e a área marrom corresponde ao quadrado do segmento representado pela cartela branca. A área do quadrado verde vale:
$$ \left ( \frac{b}{2} \right )^{2}=x\times y+\square ^{2} $$
$$ \left ( \frac{b}{2} \right )^{2}=x\times y+\left ( \frac{x-y}{2} \right )^{2} $$
Mas como sabemos que:
$$ c=x\times y $$
Então, substituindo x×y por c, vem:
$$ \left ( \frac{b}{2} \right )^{2}=c+\left ( \frac{x-y}{2} \right )^{2} $$
Ou seja, subtraindo c de (b/2)2 como apontado no passo 3:
$$ \left ( \frac{x-y}{2} \right )^{2}=\left ( \frac{b}{2} \right )^{2}-c $$
$$ \left ( \frac{x-y}{2} \right )=\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
$$ \frac{b}{2}=y+\frac{x-y}{2} $$
Substituindo o resultado do passo 4 na primeira equação, vem:
$$ \frac{b}{2}=x-\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
$$ x=\frac{b}{2}+\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2}=\frac{3}{4}+\left ( \frac{1}{2} \right )^{2} $$
A nova área resultante deste acréscimo será igual a 1:
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2}=\frac{3}{4}+\frac{1}{4}=\frac{3+1}{4}=\frac{4}{4}=1 $$
Por outro lado, a expressão:
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2} $$
É a forma fatorada de:
$$ \left ( x+\frac{1}{2} \right )^{2} $$
Basta lembrar que (x + 1/2)2 é o mesmo que (x + 1/2).(x + 1/2); assim, aplicando a propriedade distributiva na expressão acima, temos:
$$ \left ( x+\frac{1}{2} \right )\times\left ( x+\frac{1}{2} \right ) $$
$$ x^{2}+x\frac{1}{2}+\frac{1}{2}x+\left ( \frac{1}{2} \right )^{2} $$
$$ x^{2}+2x\frac{1}{2}+\left ( \frac{1}{2} \right )^{2} $$
$$ x^{2}+x+\left ( \frac{1}{2} \right )^{2} $$
Que é a forma não fatorada original. Isto posto, vem que:
$$ \left ( x+\frac{1}{2} \right )^{2}=1 $$
Tirando a raiz quadrada de ambos os membros da igualdade:
$$ \sqrt{\left ( x+\frac{1}{2} \right )^{2}}=\sqrt{1} $$
$$ x+\frac{1}{2}=1 $$
Rasgando 1/2 conforme a descrição babilônica, quer dizer, subtraindo 1/2 de cada lado da equação, temos:
$$ x+\frac{1}{2}-\frac{1}{2}=1-\frac{1}{2} $$
Finalmente, chegamos ao que os babilônios chamavam de confronto, ou seja, ao valor procurado do lado do quadrado:
$$ x=\frac{1}{2} $$
De fato, existem inúmeras plaquetas de argila babilônicas lidando com equações quadráticas, utilizando o mesmo algoritmo geométrico do exemplo acima, aplicado a lados e áreas de retângulos em 5 passos, como é o caso da tabuleta YBC3879 (um documento jurídico contendo equações quadráticas) produzida por volta de 2.000 a.C. e a YBC4663, produzida entre os séculos XIX e XVII a.C. e contendo problemas relativos à escavação de trincheiras.
 |
| Plaqueta de argila YBC3879 |
 |
| Plaqueta de argila YBC4663 |
$$ \left\{\begin{matrix}x+y=b\\ x\times y=c\end{matrix}\right. $$
Cujo desenvolvimento produz uma equação quadrática. Observe:
$$ x\times y=c\rightarrow y=\frac{c}{x} $$
Substituindo a equação acima nesta:
$$ x+y=b $$
Obtemos:
$$ x+\frac{c}{x}=b $$
$$ \frac{x^{2}+c}{x}=b $$
$$ x^{2}+c=bx $$
Finalmente, a equação quadrática fica assim:
$$ x^{2}-bx+c=0 $$
O algoritmo babilônico de 5 passos é o seguinte:
1.
Calcule a metade de b;
Considerando-se
que x e y sejam segmentos de reta, onde x
seja maior que y, e que a soma destes
segmentos vale b, então sua metade
será:
Observe: b/2
é um segmento menor que x e maior que
y. Mas quanto ele vale em relação a x e a y? Uma relação possível é esta:$$ \frac{b}{2}+\square =x $$
Onde a cartela branca é o pedaço que falta para que o segmento b/2 atinja o tamanho do segmento x. Mas sabemos que:
$$ \frac{b}{2}=\frac{x+y}{2} $$
Como enunciado pelo algoritmo no passo 1. Substituindo esta equação na anterior, temos:
$$ \frac{x+y}{2}+\square =x $$
$$ \square =x-\frac{x+y}{2} $$
$$ \square =\frac{2x-x-y}{2} $$
$$ \square =\frac{x-y}{2} $$
Ou seja, o segmento b/2 pode ser expresso como:
$$ \frac{b}{2}=x-\frac{x-y}{2} $$
Ou pode ser expresso como:
$$ \frac{b}{2}=y+\frac{x-y}{2} $$
Prosseguindo com o algoritmo, temos:
2.
Eleve o resultado ao quadrado;
O
resultado de que fala o algoritmo diz respeito ao segmento obtido no primeiro
passo, ou seja, elevar b/2 ao
quadrado. Geometricamente falando, temos:
3.
Subtraia c;
A
área verde obtida – um quadrado – não é igual àquela que seria obtida pela
multiplicação dos segmentos x e y, que formariam um retângulo de área c:
Sobrepondo as duas figuras geométricas, temos:O quadrado verde excede o retângulo em área na altura, como indicado pela região laranja, mas é inferior em área na largura, como apontado pela região azul. Comparando estas áreas, temos:
Note que a área laranja é maior que a área azul de uma quantia igual à área quadrada marrom. Em resumo: o quadrado verde é maior que o retângulo vermelho e azul de um valor igual à área marrom, e a área marrom corresponde ao quadrado do segmento representado pela cartela branca. A área do quadrado verde vale:
$$ \left ( \frac{b}{2} \right )^{2}=x\times y+\square ^{2} $$
$$ \left ( \frac{b}{2} \right )^{2}=x\times y+\left ( \frac{x-y}{2} \right )^{2} $$
Mas como sabemos que:
$$ c=x\times y $$
Então, substituindo x×y por c, vem:
$$ \left ( \frac{b}{2} \right )^{2}=c+\left ( \frac{x-y}{2} \right )^{2} $$
Ou seja, subtraindo c de (b/2)2 como apontado no passo 3:
$$ \left ( \frac{x-y}{2} \right )^{2}=\left ( \frac{b}{2} \right )^{2}-c $$
4.
Encontre a raiz quadrada usando uma tabela de quadrados;
Tirando
a raiz quadrada do lado do quadrado
marrom na equação anterior, obtemos:
$$ \sqrt{\left ( \frac{x-y}{2} \right )^{2}}=\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$$$ \left ( \frac{x-y}{2} \right )=\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
5.
Some os resultados dos passos (1) e (4) para
obter o valor de x e de y.
Vimos
no passo 1 que o segmento b/2 pode
ser expresso tanto em função de x
quanto de y:
$$ \frac{b}{2}=x-\frac{x-y}{2} $$$$ \frac{b}{2}=y+\frac{x-y}{2} $$
Substituindo o resultado do passo 4 na primeira equação, vem:
$$ \frac{b}{2}=x-\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
$$ x=\frac{b}{2}+\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
E substituindo o resultado do passo 4 na segunda
equação:
$$ y=\frac{b}{2}-\sqrt{\left ( \frac{b}{2} \right )^{2}-c} $$
Evoluindo a equação que fornece o valor de x, temos:
$$ x=\frac{b+2\sqrt{\left ( \frac{b}{2} \right )^{2}-c}}{2} $$
$$ x=\frac{b+2\sqrt{\frac{b^{2}}{4}-c}}{2} $$
$$ x=\frac{b+2\sqrt{\frac{b^{2}-4c}{4}}}{2} $$
$$ x=\frac{b+2\frac{\sqrt{b^{2}-4c}}{\sqrt{4}}}{2} $$
$$ x=\frac{b+\sqrt{b^{2}-4c}}{2} $$
E seguindo o mesmo procedimento para a equação
que fornece o valor de y chega-se a:
$$ y=\frac{b-\sqrt{b^{2}-4c}}{2} $$
Estas são as equações
quadráticas reduzidas e se assemelham muito à lei de Báskara. Também a
civilização egípcia lidava com equações algébricas, tanto lineares quanto
quadráticas, em problemas de cunho prático. Um exemplo envolvendo equações
algébricas lineares pode ser devidamente apreciado no papiro de Ahmes, datado
de cerca de 1550 a.C. e que atualmente se encontra no Museu Britânico sob as
denominações pBM10057 e pBM10058.
 |
| O papiro matemático de Ahmes |
O problema de número 28 estabelece o seguinte:
Pense em um número e some 2/3 desse
número a ele mesmo. Desta soma, subtraia 1/3 de seu valor, resultando 10; diga
qual é o seu número. Suponha que a resposta seja 10. Depois, subtraia 1/10
destes 10, obtendo 9. Então 9 foi o primeiro número pensado.
O escriba Ahmes então apresenta a seguinte "prova":
Se
o número original era 9, então 2/3 é 6, que somado resulta 15. Então, 1/3 de 15
é 5, que na subtração deixa 10. É assim que se faz.
Uma das técnicas egípcias para a solução de
equações lineares baseia-se no método da
falsa posição, já abordada no capítulo Razão e proporção, no terceiro volume desta série. Assume-se uma resposta
conveniente, mas provavelmente incorreta para encontrar a resposta que depois é
ajustada usando proporcionalidade. Em notação algébrica moderna, Ahmes faz a
seguinte proposição:
$$ x+\frac{2x}{3}-\frac{1}{3}\left ( x+\frac{2x}{3} \right )=10 $$
Atribuindo o valor 10 à incógnita, temos:
$$ x+\frac{20}{3}-\frac{1}{3}\left ( 10+\frac{20}{3} \right )=10 $$
Efetuando o mínimo múltiplo comum entre 10 e
20/3, que é 3:
$$ \frac{30+20}{3}-\frac{1}{3}\left ( \frac{30+20}{3} \right )=10 $$
Chegando a:
$$ \frac{50}{3}-\frac{1}{3}\left ( \frac{50}{3} \right )=10 $$
$$ \frac{50}{3}-\frac{50}{9}=10 $$
Obtendo o mínimo múltiplo comum dos
denominadores, vem:
$$ \frac{150-50}{9}=10 $$
Finalmente, chegamos ao resultado:
$$ \frac{100}{9}=10 $$
Este resultado, claro está, não corresponde à
resposta correta, pois 100/9 é um valor próximo, porém maior que 10; aqui entra
em operação a regra da falsa posição,
baseada no esquema geométrico a seguir:
No desenho acima, o lado AE representa o número procurado (o escriba chutou 10) como sendo a
solução da equação linear, e o lado DE
representa o resultado obtido a partir dessa estimativa (100/9). Então,
considerando o lado BC como o
resultado esperado da equação linear, que é 10, temos que o lado AC corresponde ao número que resolve o problema.
Assim, chega-se à proporção:
$$ \frac{AE}{DE}=\frac{AC}{BC} $$
Substituindo os segmentos pelos respectivos
valores:
$$ \frac{10}{\frac{100}{9}}=\frac{x}{10} $$
Desenvolvendo a proporção, temos:
$$ \frac{90}{100}=\frac{x}{10} $$
$$ 100x=900 $$
$$ x=\frac{900}{100} $$
$$ x=9 $$
$$ x=\frac{900}{100} $$
$$ x=9 $$
Portanto, a resposta ao problema é 9. De fato,
substituindo a incógnita na equação linear por 9, obtemos:
$$ x+\frac{2\left ( 9 \right )}{3}-\frac{1}{3}\left ( x+\frac{2\left ( 9 \right )}{3} \right )=10 $$
$$ x+\frac{18}{3}-\frac{1}{3}\left ( 9+\frac{18}{3} \right )=10 $$
$$ 9+6-\frac{1}{3}\left ( 9+6 \right )=10 $$
$$ 15-\frac{1}{3}\left ( 15 \right )=10 $$
$$ 15-5=10 $$
$$ 10=10 $$
A igualdade indica que 9 é o número que somado a 2/3 dele mesmo e subtraído de 1/3 dessa soma resulta 10. Os egípcios também lidavam com problemas envolvendo equações quadráticas, entre os quais é possível apreciar um exemplo no papiro de Moscou, um manuscrito datado de aproximadamente 1.850 a.C. contendo 25 problemas matemáticos e atualmente sob custódia do Museu Estadual Pushkin de Belas Artes em Moscou.
$$ V=\frac{h}{3}\left ( x^{2}+xy+y^{2} \right ) $$
Substituindo pelos valores fornecidos no enunciado, temos:
$$ V=\frac{6}{3}\left ( 4^{2}+4\times 2+2^{2} \right ) $$
$$ V=2 \left (16+8+4 \right ) $$
$$ V=2 \left (28 \right )=56 $$
Se ao invés de truncada a pirâmide fosse completa, bastaria zerar o valor da base menor na fórmula para obtermos o novo volume:
$$ V=\frac{hx^{2}}{3} $$
Supondo que a altura h da pirâmide completa fosse 9, teríamos:
$$ V=\frac{9\left (4^{2} \right )}{3}=\frac{9\left ( 16 \right )}{3}=3\left ( 16 \right )=48 $$
É possível que os egípcios tivessem conhecimento também desta fórmula, já que é preciso um entendimento bem avançado de álgebra para se obter o volume de uma pirâmide truncada partindo de outra completa; todavia, não se sabe ao certo como os egípcios descobriram esse algoritmo de cálculo. O cálculo algébrico para se chegar à fórmula do volume de uma pirâmide truncada pode ser feito intuitivamente a partir de um cubo, cujas arestas opostas são unidas entre si, conforme ilustrado em linhas pontilhadas vermelhas, a seguir:
Observe: as linhas vermelhas pontilhadas formam um total de 6 pirâmides de bases quadradas, cujas alturas correspondem à metade do lado do cubo, ou seja:
$$ altura_{p}=h=\frac{x}{2} $$
Como o volume de um cubo é a multiplicação do comprimento pela largura pela altura, temos:
$$ volume_{c}=x^{3} $$
Logo, se temos 6 pirâmides idênticas dentro do cubo, o volume de cada pirâmide corresponderá a 1/6 do volume do cubo:
$$ volume_{p}=\frac{1}{6}volume_{c}=\frac{1}{6}x^{3} $$
Podemos fazer a seguinte manipulação algébrica com a expressão acima:
$$ volume_{p}=\frac{1}{6}x^{3}=\frac{1}{3}\times x^{2}\times \frac{x}{2} $$
Como a área da face do cubo é igual a x2, que corresponde à área da base das pirâmides, e x/2 corresponde à altura h das pirâmides, o volume de cada pirâmide poderá ser expresso como:
$$ volume_{p}=\frac{hx^{2}}{3} $$
Agora que já temos o volume de uma pirâmide completa, vejamos como obter o volume de uma pirâmide truncada. Considere a figura em perspectiva, abaixo:
Esta imagem mostra uma pirâmide completa de base retangular que foi segmentada longitudinalmente, formando outras duas pirâmides completas: uma grande e outra pequena. Ao destacarmos a pirâmide pequena, resta a pirâmide truncada. E abaixo temos a vista superior dessa pirâmide completa, incluindo o corte longitudinal:
Desta vista superior, podemos encontrar a seguinte proporção, obtida por semelhança de triângulos:
$$ \frac{AQ_{2}}{AP_{2}}=\frac{Q_{1}Q_{2}}{P_{1}P_{2}}=\frac{c}{a} $$
E também esta outra proporção:
$$ \frac{AQ_{2}}{AP_{2}}=\frac{Q_{2}Q_{3}}{P_{2}P_{3}}=\frac{d}{b} $$
Donde é possível concluir que:
Agora, observando a figura em perspectiva, temos
que o volume da pirâmide truncada é igual ao volume da pirâmide completa grande
subtraído do volume da pirâmide completa pequena:
$$ V_{pt}=V_{pg}-V_{pp} $$
Como já conhecemos o volume de uma pirâmide completa, a igualdade acima pode ser reescrita da seguinte maneira:
Onde hpg
é a altura da pirâmide grande e corresponde ao segmento MA, e hpp é a
altura da pirâmide pequena e equivalente ao segmento NA. A multiplicação do comprimento pela largura da pirâmide grande
(a × b), bem como da pirâmide pequena (c × d) corresponde à área das bases, que
na fórmula original do volume foi apresentada como x2, pois a base era quadrada.
Por semelhança de triângulos, podemos
obter – a partir da imagem em perspectiva – a seguinte proporção:
$$ \frac{MA}{NA}=\frac{P_{1}M}{Q_{1}N} $$
O tamanho do segmento P1M pode ser obtido através do teorema de Pitágoras:
$$ \left ( P_{1}M \right )^{2}=\left ( \frac{a}{2} \right )^{2}+\left ( \frac{b}{2} \right )^{2}=\frac{a^{2}}{4}+\frac{b^{2}}{4} $$
Portanto, o segmento P1M vale:
$$ P_{1}M=\sqrt{\frac{a^{2}}{4}+\frac{b^{2}}{4}}=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{4}}=\frac{\sqrt{a^{2}+b^{2}}}{2} $$
Seguindo a mesma linha de raciocínio para calcular o tamanho do segmento Q1N, obtemos:
$$ \left ( Q_{1}N \right )^{2}=\left ( \frac{c}{2} \right )^{2}+\left ( \frac{d}{2} \right )^{2}=\frac{c^{2}}{4}+\frac{d^{2}}{4} $$
Resultando:
$$ Q_{1}N=\sqrt{\frac{c^{2}}{4}+\frac{d^{2}}{4}}=\frac{\sqrt{c^{2}+d^{2}}}{\sqrt{4}}=\frac{\sqrt{c^{2}+d^{2}}}{2} $$
Portanto, a proporção obtida será:
$$ \frac{MA}{NA}=\frac{P_{1}M}{Q_{1}N}=\frac{\frac{\sqrt{a^{2}+b^{2}}}{2}}{\frac{\sqrt{c^{2}+d^{2}}}{2}}=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{c^{2}+d^{2}}} $$
Se, na razão à direita da igualdade, multiplicarmos o numerador por b/b e o denominador por d/d, não alteramos em nada o seu valor:
$$ \frac{MA}{NA}=\frac{\frac{b}{b}\sqrt{a^{2}+b^{2}}}{\frac{d}{d}\sqrt{c^{2}+d^{2}}} $$
Passando os denominadores b e d para dentro das raízes, temos:
$$ \frac{MA}{NA}=\frac{b\sqrt{\frac{a^{2}+b^{2}}{b^{2}}}}{d\sqrt{\frac{c^{2}+d^{2}}{d^{2}}}}=\frac{b\sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{b^{2}}}}{d\sqrt{\frac{c^{2}}{d^{2}}+\frac{d^{2}}{d^{2}}}}=\frac{b\sqrt{\frac{a^{2}}{b^{2}}+1}}{d\sqrt{\frac{c^{2}}{d^{2}}+1}}=\frac{b\sqrt{\left (\frac{a}{b} \right )^{2}+1}}{d\sqrt{\left (\frac{c}{d} \right )^{2}+1}} $$
Mas como é válida a seguinte proporção, obtida em (1):
$$ \frac{c}{a}=\frac{d}{b} $$
Se multiplicarmos ambas as razões desta igualdade por a/d não alteraremos a proporção existente entre as mesmas, ou seja:
$$ \frac{c}{a}\times \frac{a}{d}=\frac{d}{b}\times \frac{a}{d} $$
Restando:
$$ \frac{c}{d}=\frac{a}{b} $$
Com esta nova igualdade, podemos concluir que:
$$ \sqrt{\left ( \frac{c}{d} \right )^{2}+1}=\sqrt{\left ( \frac{a}{b} \right )^{2}+1} $$
E finalmente a proporção entre as alturas das duas pirâmides completas pode ser reescrita simplificadamente como:
$$ \frac{MA}{NA}=\frac{b}{d} $$
Da equação acima pode-se obter ainda a seguinte proporção:
Vamos procurar agora uma relação entre a altura
da pirâmide truncada e as alturas das pirâmides completas; para chegar a essa relação,
devemos nos lembrar de que essa altura corresponde à altura da pirâmide grande
subtraída da altura da pirâmide pequena, ou seja:
$$ h_{pt}=h_{pg}-h_{pp}=MA-NA $$
Então, manipulando algebricamente a equação (3) sem alterar a proporção existente entre suas razões, temos:
A equação (4) pode ser reescrita como a seguinte
proporção:
$$ \frac{MA-NA}{NA}=\frac{a-c}{c} $$
Sendo MA – NA a altura da pirâmide truncada (hpt) e NA a altura da pirâmide completa pequena (hpp), temos:
De modo análogo, a partir da equação (3) temos:
$$ \frac{MA}{NA}=\frac{a}{c} $$
Sendo MA a altura da pirâmide completa grande (hpg) e MA – NA a altura da pirâmide truncada (hpt):
$$ \frac{MA}{MA-NA}=\frac{a}{a-c} $$
Ou seja:
Substituindo as equações (5) e (6) na equação
(2), temos:
$$ V_{pt}=\frac{h_{pg}\times a\times b}{3}-\frac{h_{pp}\times c\times d}{3}=\frac{\frac{h_{pt}\times a}{a-c}\times a\times b}{3}-\frac{\frac{h_{pt}\times c}{a-c}\times c\times d}{3} $$
Simplificando:
$$ V_{pt}=\frac{\frac{h_{pt}\times a^{2}\times b}{a-c}}{3}-\frac{\frac{h_{pt}\times c^{2}\times d}{a-c}}{3}=\frac{h_{pt}\times a^{2}\times b}{3\left ( a-c \right )}-\frac{h_{pt}\times c^{2}\times d}{3\left ( a-c \right )} $$
$$ V_{pt}=\frac{1}{3}\times\frac{h_{pt}}{\left (a-c \right )}\times\left [ a^{2}b-c^{2}d \right ] $$
Da proporção:
$$ \frac{c}{a}=\frac{d}{b} $$
Temos que:
$$ b=\frac{a\times d}{c} $$
Então:
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ a^{2}\frac{a\times d}{c}-c^{2}d \right ] $$
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ \frac{a^{3}d}{c}-c^{2}d \right ] $$
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ \frac{a^{3}d-c^{3}d}{c} \right ] $$
$$ V_{pt}=\frac{1}{3c}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ a^{3}d-c^{3}d \right ] $$
$$ V_{pt}=\frac{h_{pt}\times d\times \left [ a^{3}-c^{3} \right ]}{3c\times \left ( a-c \right )} $$
Lembrando que a forma fatorada da diferença de dois cubos é:
$$ \left ( a^{3}-c^{3} \right )=\left ( a-c \right )\times\left ( a^{2}+ac+c^{2} \right ) $$
Substituindo na equação anterior, vem:
$$ V_{pt}=\frac{h_{pt}\times d\times \left ( a-c \right )\times \left ( a^{2}+ac+c^{2} \right )}{3c\times \left ( a-c \right )} $$
Simplificando, obtemos:
$$ V_{pt}=\frac{h_{pt}\times d\times \left ( a^{2}+ac+c^{2} \right )}{3c} $$
Este é o volume de uma pirâmide truncada cuja base é retangular, e onde c e d são as medidas da base da pirâmide completa pequena. Se ao invés de uma pirâmide de base retangular tivermos uma pirâmide de base quadrada, as medidas c e d são iguais, ou seja, podemos afirmar que o volume de uma pirâmide truncada de base quadrada é um caso particular do volume de uma pirâmide truncada de base retangular; neste caso, a fórmula ficará reduzida a:
$$ V_{pt}=\frac{h_{pt}}{3}\times \left ( a^{2}+ac+c^{2} \right ) $$
Que é a fórmula que produz o mesmo resultado para o volume da pirâmide truncada do problema 14 no papiro de Moscou.
Do exposto, observa-se que a álgebra babilônica e egípcia envolvia problemas lineares (cuja solução era baseada na regra da falsa posição) e quadráticos (através da projeção geométrica de quadrados e retângulos). A matemática dessa época era estudada por sacerdotes e escribas especializados a serviço e benefício dos governos para os quais trabalhavam e estavam subordinados, em atendimento às demandas pertinentes, tais como: coleta de impostos, mensuração de terras para plantio ou criação de gado, construção civil, trocas comerciais, confecção de calendários baseada na movimentação dos astros e práticas ritualísticas diversas. No caso dos egípcios, a construção de pirâmides estava associada à religião, fortemente pautada na crença da vida após a morte; reservada a poucos privilegiados, a mumificação dos corpos garantia a seus legítimos possuidores todos os requisitos e recursos necessários para viver do outro lado da vida de modo semelhante ao que tinham deste lado. Para isso, contavam ainda com o Livro dos Mortos, uma coletânea de feitiços, fórmulas mágicas, orações e hinos escritos em rolos de papiros e colocados nos túmulos das múmias. O objetivo desses textos era ajudar o morto em sua viagem para o outro mundo, afastando eventuais perigos que este poderia encontrar em sua viagem para o além. A idéia central do Livro dos Mortos é o respeito à verdade e à justiça, sendo crença geral que diante da deusa Maat de nada valeriam as riquezas nem a posição social do falecido, mas que apenas os atos seriam levados em conta. Para os egípcios esse conjunto de textos era considerado como obra do deus Thoth. As fórmulas contidas nesses escritos podiam garantir ao morto uma viagem tranquila para o paraíso; com o passar do tempo esses cânticos passaram a ser grafados sobre um material de baixo custo, permitindo que qualquer pessoa pudesse tentar o acesso a uma terra bem-aventurada, o que antes só estava ao alcance do rei e da nobreza.
Depois deste prólogo, a alma fala então a Confissão Negativa e é questionada pelos deuses e pelos quarenta e dois juízes. Neste ponto, algumas informações muito específicas eram necessárias para serem justificadas pelos deuses. Era preciso conhecer os nomes dos diferentes deuses e do que eles eram responsáveis, mas também importava saber detalhes como os nomes das portas e do andar no Salão de Justiça pelos quais a alma deveria atravessar; necessitava-se até mesmo saber os nomes dos próprios pés. Quando a alma respondia a cada divindade e objeto com a resposta correta, ouvia como réplica: "Você nos conhece, passe por nós" e poderia continuar o seu trajeto, como neste trecho:
O feitiço conclui com aquilo que a alma deverá vestir durante o julgamento e como se deve recitá-lo:
Depois disso, o escriba que escreveu o feitiço felicita-se pelo trabalho bem feito e garante ao leitor que ele, o escriba, florescerá – bem como seus filhos – por sua parte em fornecer o feitiço. “Farei bem”, diz, “quando eu mesmo chegar ao julgamento e for introduzido com os reis do Alto Egito e os reis do Baixo Egito e estiver na casa de Osíris. Uma questão um milhão de vezes verdade”. Por ter fornecido o feitiço para o morto, o escriba considerou-se parte da engrenagem da vida após a morte e assim também lhe foi assegurada uma recepção favorável no submundo e sua passagem para o paraíso. Dada a importância capital do pós-vida, valia a pena para os escribas ter uma matemática avançada o suficiente para saber calcular o volume de pirâmides, pois isto envolvia: o custo para cortar e transportar a quantidade correta de pedras que preencheriam o volume da pirâmide, o total de horas-homens trabalhadas, envolvendo alimentação, abrigo e baixas por acidentes de trabalho, e ter tudo pronto enquanto o dono da obra (o faraó ou algum membro da nobreza) fosse vivo. Se esse procedimento soa obsoleto e um tanto bizarro, para os egípcios era, literalmente, uma questão de vida ou morte e, por isso mesmo, levada muito a sério.
Referências bibliográficas:
$$ 9+6-\frac{1}{3}\left ( 9+6 \right )=10 $$
$$ 15-\frac{1}{3}\left ( 15 \right )=10 $$
$$ 15-5=10 $$
$$ 10=10 $$
A igualdade indica que 9 é o número que somado a 2/3 dele mesmo e subtraído de 1/3 dessa soma resulta 10. Os egípcios também lidavam com problemas envolvendo equações quadráticas, entre os quais é possível apreciar um exemplo no papiro de Moscou, um manuscrito datado de aproximadamente 1.850 a.C. contendo 25 problemas matemáticos e atualmente sob custódia do Museu Estadual Pushkin de Belas Artes em Moscou.
 |
| Papiro de Moscou contendo o problema do volume de uma pirâmide truncada. |
O problema 14 possui uma fórmula relacionada ao volume de
uma pirâmide truncada (indicado na imagem acima), cujo enunciado é este:
Se alguém lhe diz: uma pirâmide
truncada possui 6 de altura por 4 de base e 2 de topo, você deve elevar este 4
ao quadrado; o resultado é 16. Você duplica o 4; o resultado é 8. Você eleva
este 2 ao quadrado; o resultado é 4. Você soma o 16 e o 8 e o 4; o resultado é
28. Você retira 1/3 de 6; o resultado é 2. Tome 28 duas vezes; o resultado é
56. Eis que o volume é 56. Você verá que isto é correto.
O
desenho no papiro indica a forma desta pirâmide truncada, com suas respectivas
medidas:
Traduzindo o problema para a linguagem algébrica
moderna, chamando a largura da base maior de x, a largura da base
menor de y e a altura de h, o volume fornecido corretamente
pelos egípcios seria representado através da fórmula:$$ V=\frac{h}{3}\left ( x^{2}+xy+y^{2} \right ) $$
Substituindo pelos valores fornecidos no enunciado, temos:
$$ V=\frac{6}{3}\left ( 4^{2}+4\times 2+2^{2} \right ) $$
$$ V=2 \left (16+8+4 \right ) $$
$$ V=2 \left (28 \right )=56 $$
Se ao invés de truncada a pirâmide fosse completa, bastaria zerar o valor da base menor na fórmula para obtermos o novo volume:
$$ V=\frac{hx^{2}}{3} $$
Supondo que a altura h da pirâmide completa fosse 9, teríamos:
$$ V=\frac{9\left (4^{2} \right )}{3}=\frac{9\left ( 16 \right )}{3}=3\left ( 16 \right )=48 $$
É possível que os egípcios tivessem conhecimento também desta fórmula, já que é preciso um entendimento bem avançado de álgebra para se obter o volume de uma pirâmide truncada partindo de outra completa; todavia, não se sabe ao certo como os egípcios descobriram esse algoritmo de cálculo. O cálculo algébrico para se chegar à fórmula do volume de uma pirâmide truncada pode ser feito intuitivamente a partir de um cubo, cujas arestas opostas são unidas entre si, conforme ilustrado em linhas pontilhadas vermelhas, a seguir:
Observe: as linhas vermelhas pontilhadas formam um total de 6 pirâmides de bases quadradas, cujas alturas correspondem à metade do lado do cubo, ou seja:
$$ altura_{p}=h=\frac{x}{2} $$
Como o volume de um cubo é a multiplicação do comprimento pela largura pela altura, temos:
$$ volume_{c}=x^{3} $$
Logo, se temos 6 pirâmides idênticas dentro do cubo, o volume de cada pirâmide corresponderá a 1/6 do volume do cubo:
$$ volume_{p}=\frac{1}{6}volume_{c}=\frac{1}{6}x^{3} $$
Podemos fazer a seguinte manipulação algébrica com a expressão acima:
$$ volume_{p}=\frac{1}{6}x^{3}=\frac{1}{3}\times x^{2}\times \frac{x}{2} $$
Como a área da face do cubo é igual a x2, que corresponde à área da base das pirâmides, e x/2 corresponde à altura h das pirâmides, o volume de cada pirâmide poderá ser expresso como:
$$ volume_{p}=\frac{hx^{2}}{3} $$
Agora que já temos o volume de uma pirâmide completa, vejamos como obter o volume de uma pirâmide truncada. Considere a figura em perspectiva, abaixo:
Esta imagem mostra uma pirâmide completa de base retangular que foi segmentada longitudinalmente, formando outras duas pirâmides completas: uma grande e outra pequena. Ao destacarmos a pirâmide pequena, resta a pirâmide truncada. E abaixo temos a vista superior dessa pirâmide completa, incluindo o corte longitudinal:
Desta vista superior, podemos encontrar a seguinte proporção, obtida por semelhança de triângulos:
$$ \frac{AQ_{2}}{AP_{2}}=\frac{Q_{1}Q_{2}}{P_{1}P_{2}}=\frac{c}{a} $$
E também esta outra proporção:
$$ \frac{AQ_{2}}{AP_{2}}=\frac{Q_{2}Q_{3}}{P_{2}P_{3}}=\frac{d}{b} $$
Donde é possível concluir que:
| $$ \frac{Q_{1}Q_{2}}{P_{1}P_{2}}=\frac{Q_{2}Q_{3}}{P_{2}P_{3}}\Rightarrow \frac{c}{a}=\frac{d}{b} $$
|
(1)
|
$$ V_{pt}=V_{pg}-V_{pp} $$
Como já conhecemos o volume de uma pirâmide completa, a igualdade acima pode ser reescrita da seguinte maneira:
| $$ V_{pt}=\frac{h_{pg}\times a\times b}{3}-\frac{h_{pp}\times c\times d}{3} $$
|
(2)
|
$$ \frac{MA}{NA}=\frac{P_{1}M}{Q_{1}N} $$
O tamanho do segmento P1M pode ser obtido através do teorema de Pitágoras:
$$ \left ( P_{1}M \right )^{2}=\left ( \frac{a}{2} \right )^{2}+\left ( \frac{b}{2} \right )^{2}=\frac{a^{2}}{4}+\frac{b^{2}}{4} $$
Portanto, o segmento P1M vale:
$$ P_{1}M=\sqrt{\frac{a^{2}}{4}+\frac{b^{2}}{4}}=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{4}}=\frac{\sqrt{a^{2}+b^{2}}}{2} $$
Seguindo a mesma linha de raciocínio para calcular o tamanho do segmento Q1N, obtemos:
$$ \left ( Q_{1}N \right )^{2}=\left ( \frac{c}{2} \right )^{2}+\left ( \frac{d}{2} \right )^{2}=\frac{c^{2}}{4}+\frac{d^{2}}{4} $$
Resultando:
$$ Q_{1}N=\sqrt{\frac{c^{2}}{4}+\frac{d^{2}}{4}}=\frac{\sqrt{c^{2}+d^{2}}}{\sqrt{4}}=\frac{\sqrt{c^{2}+d^{2}}}{2} $$
Portanto, a proporção obtida será:
$$ \frac{MA}{NA}=\frac{P_{1}M}{Q_{1}N}=\frac{\frac{\sqrt{a^{2}+b^{2}}}{2}}{\frac{\sqrt{c^{2}+d^{2}}}{2}}=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{c^{2}+d^{2}}} $$
Se, na razão à direita da igualdade, multiplicarmos o numerador por b/b e o denominador por d/d, não alteramos em nada o seu valor:
$$ \frac{MA}{NA}=\frac{\frac{b}{b}\sqrt{a^{2}+b^{2}}}{\frac{d}{d}\sqrt{c^{2}+d^{2}}} $$
Passando os denominadores b e d para dentro das raízes, temos:
$$ \frac{MA}{NA}=\frac{b\sqrt{\frac{a^{2}+b^{2}}{b^{2}}}}{d\sqrt{\frac{c^{2}+d^{2}}{d^{2}}}}=\frac{b\sqrt{\frac{a^{2}}{b^{2}}+\frac{b^{2}}{b^{2}}}}{d\sqrt{\frac{c^{2}}{d^{2}}+\frac{d^{2}}{d^{2}}}}=\frac{b\sqrt{\frac{a^{2}}{b^{2}}+1}}{d\sqrt{\frac{c^{2}}{d^{2}}+1}}=\frac{b\sqrt{\left (\frac{a}{b} \right )^{2}+1}}{d\sqrt{\left (\frac{c}{d} \right )^{2}+1}} $$
Mas como é válida a seguinte proporção, obtida em (1):
$$ \frac{c}{a}=\frac{d}{b} $$
Se multiplicarmos ambas as razões desta igualdade por a/d não alteraremos a proporção existente entre as mesmas, ou seja:
$$ \frac{c}{a}\times \frac{a}{d}=\frac{d}{b}\times \frac{a}{d} $$
Restando:
$$ \frac{c}{d}=\frac{a}{b} $$
Com esta nova igualdade, podemos concluir que:
$$ \sqrt{\left ( \frac{c}{d} \right )^{2}+1}=\sqrt{\left ( \frac{a}{b} \right )^{2}+1} $$
E finalmente a proporção entre as alturas das duas pirâmides completas pode ser reescrita simplificadamente como:
$$ \frac{MA}{NA}=\frac{b}{d} $$
Da equação acima pode-se obter ainda a seguinte proporção:
| $$ \frac{MA}{NA}=\frac{b}{d}=\frac{a}{c} $$ |
(3)
|
$$ h_{pt}=h_{pg}-h_{pp}=MA-NA $$
Então, manipulando algebricamente a equação (3) sem alterar a proporção existente entre suas razões, temos:
| $$ \frac{MA-NA}{NA}=\frac{b-d}{d}=\frac{a-c}{c} $$
|
(4)
|
$$ \frac{MA-NA}{NA}=\frac{a-c}{c} $$
Sendo MA – NA a altura da pirâmide truncada (hpt) e NA a altura da pirâmide completa pequena (hpp), temos:
| $$ \frac{h_{pt}}{h_{pp}}=\frac{a-c}{c}\Rightarrow h_{pp}=\frac{h_{pt}\times c}{a-c} $$ |
(5)
|
$$ \frac{MA}{NA}=\frac{a}{c} $$
Sendo MA a altura da pirâmide completa grande (hpg) e MA – NA a altura da pirâmide truncada (hpt):
$$ \frac{MA}{MA-NA}=\frac{a}{a-c} $$
Ou seja:
| $$ \frac{h_{pg}}{h_{pt}}=\frac{a}{a-c}\Rightarrow h_{pg}=\frac{h_{pt}\times a}{a-c} $$ |
(6)
|
$$ V_{pt}=\frac{h_{pg}\times a\times b}{3}-\frac{h_{pp}\times c\times d}{3}=\frac{\frac{h_{pt}\times a}{a-c}\times a\times b}{3}-\frac{\frac{h_{pt}\times c}{a-c}\times c\times d}{3} $$
Simplificando:
$$ V_{pt}=\frac{\frac{h_{pt}\times a^{2}\times b}{a-c}}{3}-\frac{\frac{h_{pt}\times c^{2}\times d}{a-c}}{3}=\frac{h_{pt}\times a^{2}\times b}{3\left ( a-c \right )}-\frac{h_{pt}\times c^{2}\times d}{3\left ( a-c \right )} $$
$$ V_{pt}=\frac{1}{3}\times\frac{h_{pt}}{\left (a-c \right )}\times\left [ a^{2}b-c^{2}d \right ] $$
Da proporção:
$$ \frac{c}{a}=\frac{d}{b} $$
Temos que:
$$ b=\frac{a\times d}{c} $$
Então:
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ a^{2}\frac{a\times d}{c}-c^{2}d \right ] $$
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ \frac{a^{3}d}{c}-c^{2}d \right ] $$
$$ V_{pt}=\frac{1}{3}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ \frac{a^{3}d-c^{3}d}{c} \right ] $$
$$ V_{pt}=\frac{1}{3c}\times \frac{h_{pt}}{\left ( a-c \right )}\times \left [ a^{3}d-c^{3}d \right ] $$
$$ V_{pt}=\frac{h_{pt}\times d\times \left [ a^{3}-c^{3} \right ]}{3c\times \left ( a-c \right )} $$
Lembrando que a forma fatorada da diferença de dois cubos é:
$$ \left ( a^{3}-c^{3} \right )=\left ( a-c \right )\times\left ( a^{2}+ac+c^{2} \right ) $$
Substituindo na equação anterior, vem:
$$ V_{pt}=\frac{h_{pt}\times d\times \left ( a-c \right )\times \left ( a^{2}+ac+c^{2} \right )}{3c\times \left ( a-c \right )} $$
Simplificando, obtemos:
$$ V_{pt}=\frac{h_{pt}\times d\times \left ( a^{2}+ac+c^{2} \right )}{3c} $$
Este é o volume de uma pirâmide truncada cuja base é retangular, e onde c e d são as medidas da base da pirâmide completa pequena. Se ao invés de uma pirâmide de base retangular tivermos uma pirâmide de base quadrada, as medidas c e d são iguais, ou seja, podemos afirmar que o volume de uma pirâmide truncada de base quadrada é um caso particular do volume de uma pirâmide truncada de base retangular; neste caso, a fórmula ficará reduzida a:
$$ V_{pt}=\frac{h_{pt}}{3}\times \left ( a^{2}+ac+c^{2} \right ) $$
Que é a fórmula que produz o mesmo resultado para o volume da pirâmide truncada do problema 14 no papiro de Moscou.
Do exposto, observa-se que a álgebra babilônica e egípcia envolvia problemas lineares (cuja solução era baseada na regra da falsa posição) e quadráticos (através da projeção geométrica de quadrados e retângulos). A matemática dessa época era estudada por sacerdotes e escribas especializados a serviço e benefício dos governos para os quais trabalhavam e estavam subordinados, em atendimento às demandas pertinentes, tais como: coleta de impostos, mensuração de terras para plantio ou criação de gado, construção civil, trocas comerciais, confecção de calendários baseada na movimentação dos astros e práticas ritualísticas diversas. No caso dos egípcios, a construção de pirâmides estava associada à religião, fortemente pautada na crença da vida após a morte; reservada a poucos privilegiados, a mumificação dos corpos garantia a seus legítimos possuidores todos os requisitos e recursos necessários para viver do outro lado da vida de modo semelhante ao que tinham deste lado. Para isso, contavam ainda com o Livro dos Mortos, uma coletânea de feitiços, fórmulas mágicas, orações e hinos escritos em rolos de papiros e colocados nos túmulos das múmias. O objetivo desses textos era ajudar o morto em sua viagem para o outro mundo, afastando eventuais perigos que este poderia encontrar em sua viagem para o além. A idéia central do Livro dos Mortos é o respeito à verdade e à justiça, sendo crença geral que diante da deusa Maat de nada valeriam as riquezas nem a posição social do falecido, mas que apenas os atos seriam levados em conta. Para os egípcios esse conjunto de textos era considerado como obra do deus Thoth. As fórmulas contidas nesses escritos podiam garantir ao morto uma viagem tranquila para o paraíso; com o passar do tempo esses cânticos passaram a ser grafados sobre um material de baixo custo, permitindo que qualquer pessoa pudesse tentar o acesso a uma terra bem-aventurada, o que antes só estava ao alcance do rei e da nobreza.
Uma das passagens mais simbólicas e conhecidas do Livro dos Mortos é o cântico 125: Julgamento, que descreve o
ritual de pesagem do coração, onde se pode apreciar um pedaço do prólogo,
abaixo:
“Salve, grande deus, Senhor da
Justiça! Eu vim a ti, meu senhor, para que te mostres a mim para que eu possa
ver a tua beleza, porque eu te conheço e conheço o teu nome e conheço os nomes
dos quarenta e dois daqueles deuses que estão contigo neste Salão de Justiça,
que vivem dos que amam o mal e que bebem seu sangue naquele dia da contagem de
indivíduos na presença de Wennefer [outro nome para Osíris]. Eis o duplo filho
das tranças das Canções; O Senhor da Verdade é o seu nome. Eis que eu vim a
vós, trouxe-vos a verdade; Eu não fiz falsidade contra os homens, eu não
empobreci meus associados, eu não fiz nada de errado no Lugar da Verdade, eu
não aprendi o que não é ...[etc.]”
Depois deste prólogo, a alma fala então a Confissão Negativa e é questionada pelos deuses e pelos quarenta e dois juízes. Neste ponto, algumas informações muito específicas eram necessárias para serem justificadas pelos deuses. Era preciso conhecer os nomes dos diferentes deuses e do que eles eram responsáveis, mas também importava saber detalhes como os nomes das portas e do andar no Salão de Justiça pelos quais a alma deveria atravessar; necessitava-se até mesmo saber os nomes dos próprios pés. Quando a alma respondia a cada divindade e objeto com a resposta correta, ouvia como réplica: "Você nos conhece, passe por nós" e poderia continuar o seu trajeto, como neste trecho:
Eu não vou deixar você pisar em
mim, diz o andar deste Salão de Justiça.
Por que
não? Eu sou puro.
Porque eu não sei os nomes de seus
pés com que você pisaria em mim. Diga-os a mim.
’A
imagem secreta de Há’ é o nome do meu pé direito, 'Flor de Hathor' é o nome do
meu pé esquerdo.
Você nos conhece, passe por nós.
O feitiço conclui com aquilo que a alma deverá vestir durante o julgamento e como se deve recitá-lo:
“O procedimento correto neste Salão
de Justiça: deve-se pronunciar este feitiço puro e limpo e vestido com roupas
brancas e sandálias, pintado com tinta de olho preta e ungido com mirra.
Ser-lhe-ão oferecidas carne e aves de capoeira, incenso, pão, cerveja e ervas,
quando tiveres colocado este procedimento escrito num chão limpo de ocre
coberto de terra, sobre o qual nenhum porco ou gado pequeno pisou.”
Depois disso, o escriba que escreveu o feitiço felicita-se pelo trabalho bem feito e garante ao leitor que ele, o escriba, florescerá – bem como seus filhos – por sua parte em fornecer o feitiço. “Farei bem”, diz, “quando eu mesmo chegar ao julgamento e for introduzido com os reis do Alto Egito e os reis do Baixo Egito e estiver na casa de Osíris. Uma questão um milhão de vezes verdade”. Por ter fornecido o feitiço para o morto, o escriba considerou-se parte da engrenagem da vida após a morte e assim também lhe foi assegurada uma recepção favorável no submundo e sua passagem para o paraíso. Dada a importância capital do pós-vida, valia a pena para os escribas ter uma matemática avançada o suficiente para saber calcular o volume de pirâmides, pois isto envolvia: o custo para cortar e transportar a quantidade correta de pedras que preencheriam o volume da pirâmide, o total de horas-homens trabalhadas, envolvendo alimentação, abrigo e baixas por acidentes de trabalho, e ter tudo pronto enquanto o dono da obra (o faraó ou algum membro da nobreza) fosse vivo. Se esse procedimento soa obsoleto e um tanto bizarro, para os egípcios era, literalmente, uma questão de vida ou morte e, por isso mesmo, levada muito a sério.
Referências bibliográficas:
[1]
|
Hoyrup, J. “Old Babylonian 'algebra' and what it teaches us about possible
kinds of mathematics”, ICM Satellite Conference, Mathematics in ancient
times, Kerala School of Mathematics, 2010.
|
[2]
|
Clagett, M. "Ancient Egyptian Science: A Source Book. Volume 3:
Ancient Egyptian Mathematics", Memoirs of the American Philosophical
Society 232, Philadelphia: American Philosophical Society, 1999.
|
[3]
|
Katz, V. J. “A history of mathematics – an introduction”,
Addison-Wesley, third edition, 2013.
|
[4]
|
Friberg, J. “A Geometric Algorithm with Solutions to Quadratic
Equations in a Sumerian Juridical Document from Ur III Umma”, Cuneiform
Digital Library Journal 2009:3.
|
[5]
|
Hoyrup, J. “Pre-modern ‘algebras’: a concise survey of that which was
shaped into the technique and discipline we know”, The way through science
and philosophy: Essays in honour of Stig Andur Pedersen, pp. 1 – 15, London:
College Publications, 2006.
|