|
| Ilustração de Edmund Dulac para uma edição de 1908 do livro “As 1001 noites” |
A civilização grega começou lidando com problemas
algébricos através da geometria; Tales de Mileto (~624 a.C. – 546 a.C.) é
considerado por Aristóteles como o primeiro filósofo da tradição grega, reconhecido
por romper com a mitologia para
explicar o mundo e o universo, substituindo-a por teorias e hipóteses para justificar
os fenômenos naturais. Considerava que o princípio originador da natureza e da
natureza da matéria provinha de uma única substância: a água. Na matemática, supõe-se
que Tales tenha estudado com sacerdotes egípcios e seus métodos de tentativa e
erro para a solução de problemas matemáticos e astronômicos. Logo, ele superou
seus professores e começou a questionar como os números combinavam-se entre si,
acreditando que o método egípcio carecia de elegância e verificação. É também a
primeira pessoa conhecida a aplicar o raciocínio dedutivo à geometria, através
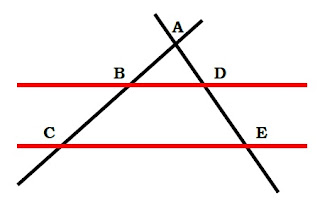
do qual chegaria ao que hoje é conhecido por Teorema de Tales. Observe:
Se dois segmentos de reta interceptam-se em um
ponto A e são cortados por duas
retas paralelas entre si, os triângulos formados por essa configuração e suas
medidas respeitam a relação entre as razões
abaixo:
$$ \frac{BD}{CE}=\frac{AB}{AC}=\frac{AD}{AE} $$
Esta semelhança
de triângulos era amplamente utilizada pelos egípcios para a solução de
problemas algébricos lineares através da regra
da falsa posição, mas Tales aplicou-a também para calcular a altura de
pirâmides. Observe a figura a seguir:
Nesta imagem temos uma pirâmide e uma vara, cuja
altura é conhecida e vale 10,5. Com a luz do Sol, tanto a pirâmide quanto a
vara projetam suas sombras no chão. Medindo o tamanho das projeções de suas sombras
e aplicando o teorema de Tales, temos
a seguinte relação por semelhança entre os triângulos ABC e DEF:
$$ \frac{Altura_{piramide}}{Altura_{vara}}=\frac{Sombra_{piramide}}{Sombra_{vara}} $$
Ou seja:
$$ \frac{x}{10,5}=\frac{30}{15} $$
Resolvendo a igualdade, vem:
$$ 15x=10,5\times 30 $$
$$ 15x=315 $$
$$ x=\frac{315}{15}=21 $$
Portanto, a altura da pirâmide vale 21. Outro grego que se
valeu da geometria para solucionar problemas que resolvemos por álgebra foi
Euclides. Em sua obra Elementos, no
livro II, proposição 5, temos:
Se uma reta é cortada em partes
iguais e desiguais, o retângulo contido pelas partes desiguais do todo, junto
com o quadrado contido pela reta entre os pontos da seção, é igual ao quadrado
contido pela metade.
A solução desta proposição dada por Euclides é como segue:
Para que uma linha reta AB seja cortada em segmentos iguais em C e em segmentos desiguais em D, digo que o retângulo contido por AD, DB juntamente com o quadrado em CD é igual ao quadrado em CB.
A
seguir, demonstra-se sua solução geometricamente, iniciando com o segmento de
reta AB dividido em partes iguais em
C e em partes desiguais em D:
O
resultado obtido até aqui está indicado na figura a seguir, acrescido do gnômon NOP. Em geometria, gnômon
corresponde à parte remanescente de um paralelogramo após a retirada de outro
similar que continha um de seus ângulos. Neste caso, o gnômon NOP representa o
paralelogramo CEFB retirado de LEGH, restando a soma das áreas de três
paralelogramos: CLHD com DHMB com HGFM:
Em
resumo, Euclides afirma que a área do paralelogramo AKHD somado à área do quadrado LEGH
iguala-se à área do quadrado CEFB:
$$ Area\left ( AKHD \right )+Area\left ( LEGH \right )=Area\left ( CEFB \right ) $$
Podemos representar este problema proposto por Euclides como uma multiplicação de lados para obtenção de áreas, da seguinte forma:
$$ \left ( AD\times AK \right )+\left ( LH\times LE \right )=\left ( CB\times CE \right ) $$
Chamando o tamanho do segmento AD de a e sabendo que DB = AK e chamando seus tamanhos de b, temos:
Com base nestas considerações, é possível
observar que LH = LE e que estes segmentos medem:
$$ \left ( \frac{a+b}{2}-b \right ) $$
E também que CB = CE e que estes segmentos medem:
$$ \left ( \frac{a+b}{2} \right ) $$
Desta forma, a proposição de Euclides é o equivalente geométrico da identidade algébrica:
$$ ab+\left [ \left ( \frac{a+b}{2}-b \right )\times \left ( \frac{a+b}{2}-b \right ) \right ]=\left [ \left ( \frac{a+b}{2} \right )\times \left ( \frac{a+b}{2} \right ) \right ] $$
Ou seja:
$$ ab+\left ( \frac{a+b}{2}-b \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
Desenvolvendo, vem:
$$ ab+\left ( \frac{a+b-2b}{2} \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
$$ ab+\left ( \frac{a-b}{2} \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
$$ ab+\frac{\left ( a-b \right )^{2}}{4}=\frac{\left ( a+b \right )^{2}}{4} $$
$$ ab+\frac{a^{2}-2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
$$ \frac{4ab+a^{2}-2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
$$ \frac{a^{2}+2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
Esta igualdade prova algebricamente o que Euclides provou por meio da geometria, ao afirmar que a área do paralelogramo AKHD somado à área do quadrado LEGH iguala-se à área do quadrado CEFB.
Ao contrário de Euclides e de outros geômetras gregos, como Arquimedes e Apolônio, Diofanto de Alexandria inaugura um novo tipo de matemática distanciada da estrutura lógica e dedutiva de seus conterrâneos, ao tratar problemas aritméticos e algébricos por si mesmos, sem aplicação da geometria e sem exposição dedutiva, antes aplicando uma álgebra sincopada, em que algum simbolismo é utilizado, ainda que ausentes as características da álgebra simbólica moderna. Assim, por exemplo, aquilo que escrevemos algebricamente como:
$$ x^{3}-2x^{2}+10x-1=5 $$
Apesar de não demonstrado, toda a construção geométrica
aplicada na solução é obtida com a utilização do compasso e da régua. Em
seguida, Euclides começa a descrever sua solução:
Para que o quadrado CEFB seja descrito em CB, e sejam unidos. Através de D, que o segmento de reta DG seja traçado paralelamente a CE ou BF. Através de H
novamente deixe que o segmento de reta KM
seja desenhado paralelamente a AB ou
EF, e novamente através de A deixe que o segmento de reta AK seja desenhado paralelamente a CL ou BM. Então, como o complemento CH
é igual ao complemento HF, adiciona-se
DM a cada um. Portanto, o todo CM é igual ao todo DF. Mas CM é igual a AL, uma vez que AC também é igual a CB;
portanto AL também é igual a DF. Faça CH ser adicionado a cada um. Portanto, o todo AH é igual ao gnômon NOP.
Prossegue Euclides:
Mas AH é o retângulo AD, DB, para DH sendo igual a DB,
portanto o gnômon NOP também é igual
ao retângulo AD, DB. Deixe LG, que é igual ao quadrado em CD,
ser adicionado a cada um; Portanto o gnômon NOP e LG são iguais ao
retângulo contido por AD, DB e o quadrado em CD. Mas o gnômon NOP e LG são o quadrado inteiro CEFB, que é descrito em CB; Portanto, o retângulo contido por AD, DB juntamente com o quadrado em CD é igual ao quadrado em CB.
$$ Area\left ( AKHD \right )+Area\left ( LEGH \right )=Area\left ( CEFB \right ) $$
Podemos representar este problema proposto por Euclides como uma multiplicação de lados para obtenção de áreas, da seguinte forma:
$$ \left ( AD\times AK \right )+\left ( LH\times LE \right )=\left ( CB\times CE \right ) $$
Chamando o tamanho do segmento AD de a e sabendo que DB = AK e chamando seus tamanhos de b, temos:
$$ \left ( \frac{a+b}{2}-b \right ) $$
E também que CB = CE e que estes segmentos medem:
$$ \left ( \frac{a+b}{2} \right ) $$
Desta forma, a proposição de Euclides é o equivalente geométrico da identidade algébrica:
$$ ab+\left [ \left ( \frac{a+b}{2}-b \right )\times \left ( \frac{a+b}{2}-b \right ) \right ]=\left [ \left ( \frac{a+b}{2} \right )\times \left ( \frac{a+b}{2} \right ) \right ] $$
Ou seja:
$$ ab+\left ( \frac{a+b}{2}-b \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
Desenvolvendo, vem:
$$ ab+\left ( \frac{a+b-2b}{2} \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
$$ ab+\left ( \frac{a-b}{2} \right )^{2}=\left ( \frac{a+b}{2} \right )^{2} $$
$$ ab+\frac{\left ( a-b \right )^{2}}{4}=\frac{\left ( a+b \right )^{2}}{4} $$
$$ ab+\frac{a^{2}-2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
$$ \frac{4ab+a^{2}-2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
$$ \frac{a^{2}+2ab+b^{2}}{4}=\frac{a^{2}+2ab+b^{2}}{4} $$
Esta igualdade prova algebricamente o que Euclides provou por meio da geometria, ao afirmar que a área do paralelogramo AKHD somado à área do quadrado LEGH iguala-se à área do quadrado CEFB.
Ao contrário de Euclides e de outros geômetras gregos, como Arquimedes e Apolônio, Diofanto de Alexandria inaugura um novo tipo de matemática distanciada da estrutura lógica e dedutiva de seus conterrâneos, ao tratar problemas aritméticos e algébricos por si mesmos, sem aplicação da geometria e sem exposição dedutiva, antes aplicando uma álgebra sincopada, em que algum simbolismo é utilizado, ainda que ausentes as características da álgebra simbólica moderna. Assim, por exemplo, aquilo que escrevemos algebricamente como:
$$ x^{3}-2x^{2}+10x-1=5 $$
Diofanto teria escrito:
$$ K^{\Upsilon }\bar{\alpha }\varsigma \bar{\iota }\Psi \Delta ^{\Upsilon }\bar{\beta }M\bar{\alpha }\iota\sigma M\bar{\varepsilon } $$
Onde os símbolos representam o seguinte:
Símbolo
|
Significado
|
| $$ \bar{\alpha } $$ |
Representa o número 1
|
| $$ \bar{\beta } $$ |
Representa o número 2
|
| $$ \bar{\varepsilon } $$ |
Representa o número 5
|
| $$ \bar{\iota } $$ |
Representa o número 10
|
| $$ \varsigma $$ |
A incógnita ou variável, representa o x
|
| $$ \iota\sigma $$ |
Abreviatura de ισος, representa o símbolo de igual (=)
|
| $$ \Psi $$ |
Representa a subtração para tudo que o segue, até ισ
|
| $$ M $$ |
Representa uma constante
|
| $$ \Delta ^{\Upsilon } $$ |
Do grego δυυναμις, dinâmis,
representa o x2
|
| $$ K^{\Upsilon } $$ |
Do grego κυβος, cubus,
representa o x3
|
Outros símbolos utilizados pelo matemático estão
indicados abaixo:
Símbolo
|
Significado
|
| $$ \Delta ^{\Upsilon }\Delta $$ |
Representa o x4
|
| $$ \Delta K^{\Upsilon } $$ |
Representa o x5
|
| $$ K^{\Upsilon }K $$ |
Representa o x6
|
Na obra de Diofanto não existia um símbolo para
a soma, de modo que os termos positivos da equação eram simplesmente
justapostos; também, os termos negativos eram todos agrupados após o Ψ (esta letra de fato aparece de cabeça para baixo em sua obra). Desta
forma, os termos positivos ou somados (o x3
e o 10x) estão agrupados, onde x3 é:
$$ K^{\Upsilon }\bar{\alpha } $$
E 10x
está indicado como:
$$ \varsigma \bar{\iota } $$
Os termos negativos ou subtraídos da equação (o -2x2 e o -1) estão agrupados após o Ψ até
aquilo que Diofanto define como um sinal de igual, ou seja, ισ. Assim, -2x2 está indicado por:
$$ \Delta ^{\Upsilon } \bar{\beta } $$
E o -1,
por ser uma constante negativa, está indicado por:
$$ M\bar{\alpha } $$
Ambos os termos são negativos pela indicação do símbolo Ψ. E finalmente o
resultado é igual (ισ)
à constante 5, representada por Με.
Quase nada se conhece da vida de Diofanto e até mesmo a época em que viveu é
incerta; estimativas baseiam-se no fato dele próprio citar Hipsicles (astrônomo
e geômetra grego nascido em Alexandria) que viveu por volta de 180 a.C. e que também
é citado por Téon de Alexandria, que viveu de 335 a 395 d.C., de modo que aceita-se
que Diofanto tenha vivido entre 200 e 280 d.C. Sua fama é devida
basicamente por ter escrito 13 livros
conhecidos por Arithmetica, uma
coleção de 130 problemas envolvendo equações de diversos tipos. Por exemplo,
ele estava interessado nas soluções numéricas de equações determinadas e
indeterminadas, estas últimas solucionadas por um método hoje conhecido como análise diofantina. Destes livros,
apenas 6 originais gregos sobreviveram, além de outros 4 traduzidos para o
árabe. Apesar de nada se saber sobre sua vida, deduz-se com que idade veio a
falecer em função de um problema algébrico que segundo a tradição foi inscrito
em sua lápide, cujos termos são estes:
Deus lhe concedeu ser um menino pela sexta parte de sua vida, e
adicionando uma duodécima parte a isso, vestiu suas bochechas com barba; Acendeu
a luz do casamento depois de uma sétima parte, e cinco anos depois o matrimônio
lhe concedeu um filho. Infelizmente! Miserável filho tardio; Após atingir a
metade da vida de seu pai, o Destino o arrebatou. Depois de consolar seu
sofrimento com a ciência dos números por quatro anos, ele encerrou sua vida.
$$ x=\frac{x}{6}+\frac{x}{12}+\frac{x}{7}+5+\frac{x}{2}+4 $$
Onde x é a idade de Diofanto.
Resolvendo a equação, temos:
$$ x=\frac{14x+7x+12x+420+42x+336}{84} $$
$$ 84x=14x+7x+12x+420+42x+336 $$
$$ 84x-14x-7x-12x-42x=420+336 $$
$$ 9x=756 $$
$$ x=\frac{756}{9}=84 $$
Diofanto é considerado por muitos como o 'pai da
álgebra', em parte por ter sido responsável pela introdução do simbolismo ao
tema. Este título de paternidade, porém, é igualmente atribuído a outro
matemático: o persa al-Khwarizmi. Abu Abdullah Muhammad Ibn Musa Al-Khwarizmi
(seu nome completo) viveu por volta de 800-847 d.C., mas estas datas não são
precisas. O epíteto “al-Khwarizm” refere-se ao local de seu nascimento,
Khwarizm ou Khorezm, localizada ao sul do delta do rio Amu Darya e do Mar do
Aral, na Ásia central.
 |
| Estátua pictórica de al-Khwarizmi, localizada nos portões ocidentais (Ata Darwaza) da cidade de Khiva, no Uzbequistão. |
Al-Khwarizm cresceu próximo a Bagdá, sob o
reinado do califa al-Mamun (que durou de 813-833 d.C.), um grande promotor da
ciência. Conta-se que al-Mamun teve um sonho no qual Aristóteles apareceu para
ele; depois disso, o califa resolveu traduzir para o árabe todas as obras
gregas que pôde adquirir. É dessa época que surgem o Almagesto de Ptolomeu e uma versão completa do Elementos de Euclides. Segundo a tradição, os originais gregos
foram trazidos a Bagdá através de tratados com o país de Roma (que era o nome
dado na época ao império Bizantino, e com quem mantinham uma paz “inquieta”)
por uma delegação enviada por al-Mamun. É interessante notar que antes dele,
seu pai – o califa al-Rashid, cujo reinado foi de 786-809 d.C. – já iniciara
uma tradução rigorosa de clássicos matemáticos em grego e sânscrito para o
árabe, entre os quais algumas partes do Elementos,
bem como mandou erigir a Casa da
Sabedoria, um centro intelectual que floresceu sob o reinado do prestimoso
filho e do qual al-Khwarizmi foi um membro ativo, tanto que boa parte de sua
obra é dedicada a al-Mamun. Além de compilar as mais antigas tabelas
astronômicas conhecidas até então, al-Khwarizmi também compôs o mais antigo
trabalho de aritmética e de álgebra.
 |
| Foto moderna de um pátio na Casa da Sabedoria, construída sob o reinado de al-Rashid. |
A versão árabe completa de seu trabalho mais
famoso consiste de três volumes: um de álgebra propriamente, cobrindo suas
regras com 40 exercícios, uma seção sobre a regra de três e problemas sobre
mensurações (em que delineia as regras para o cálculo de áreas e volumes), e
uma longa seção compreendendo problemas e soluções relativos a heranças,
envolvendo aritmética simples e equações lineares. As leis de herança recebem o
devido tratamento no Quran (que
significa literalmente 'a recitação'),
que é nada mais que o principal texto religioso do Islã, e que os muçulmanos
creditam como tendo sido uma revelação de Alá.
 |
| Emblema do Quran |
Legislando sobre o casamento, divórcio e herança, lida com
complicadas partilhas envolvendo razões em diferentes circunstâncias ou
condições, como no exemplo abaixo:
Alá, portanto, lhe determina quanto
aos seus filhos (herança): ao varão uma porção igual à de duas varoas: se
apenas filhas, duas ou mais, a parte que lhes cabe é dois terços da herança; se
apenas uma, recebe a metade. Para os pais, uma sexta parte da herança para cada
um, se os filhos forem falecidos; se não há filhos e os pais são os únicos
herdeiros, a mãe recebe a terça parte; se o falecido deixou irmãos (ou irmãs),
a mãe recebe a sexta parte. (A distribuição em todo caso ocorre) após o
pagamento de legados e dívidas. Você não sabe se seus pais ou seus filhos estão
mais próximos de você em benefícios. Estas são as partes estabelecidas e
ordenadas por Alá, e Alá é Todo-Conhecedor, Todo Sábio. Do que suas esposas
deixarem, sua participação é metade, se elas não tiveram nenhum filho, mas se
elas tiveram uma criança, você recebe a quarta parte, após o pagamento de
legados e dívidas. Do que você deixar, elas recebem a quarta parte, se você não
teve nenhum filho; mas se você teve uma criança, elas recebem a oitava parte, após
o pagamento de legados e dívidas. Se o homem ou mulher cuja herança está em
questão, não deixaram ascendentes nem descendentes, mas deixaram um irmão ou
uma irmã, cada um dos dois recebe uma sexta parte; Mas se houver mais que dois
irmãos, eles compartilharão a terça parte, após o pagamento de legados e
dívidas; De modo que nenhuma perda seja causada (a qualquer um). Assim é
ordenado por Alá; E Alá de tudo está sabendo, assaz tolerante.
Seja como for, é no primeiro volume, cujo título é Kitab al-muhtasar fih isab al-jabr wa
al-muqabala, que a resolução de
problemas algébricos forneceu as maiores contribuições de al-Khwarizmi à matemática.
O termo al-jabr em árabe significa colocar junto, restaurar, e deu origem ao termo álgebra. No dicionário encontramos até um significado (agora em
desuso) para a palavra algebrista,
que além de ser uma pessoa versada em álgebra, na idade média era aquele que
tratava de fraturas ou deslocação de ossos, coerente com o significado árabe de
restauração, mas era utilizada por al-Khwarizmi em conjunto com a movimentação
de quantidades subtraídas para o outro lado de uma equação. E o termo al-muqabala significa confrontação, e era usado para combinar
termos semelhantes em lados opostos da equação. Estas duas palavras, além de
outras – como ikmal (concluindo) e radd (retornando) – foram aplicadas de
diferentes maneiras, para nomear os passos do processo algébrico. De fato,
al-Khwarizmi principia seu livro cobrindo as definições e regras da álgebra,
para em seguida tratar dos problemas. Uma solução algébrica consistia de três
passos:
Ø
Estabelecer uma equação em termos de números
algébricos;
Ø
Simplificar a equação para um dos seis tipos
padronizados;
Ø
Aplicar o procedimento adequado para obter a
resposta.
Os termos de uma equação eram declarados através do verbo adala (ser igual a ou equilibrar),
e os três tipos de números algébricos eram definidos como:
Tipo
|
Tradução
|
Transcrição simbólica
|
măl
|
Soma de dinheiro,
propriedade...
|
x2
|
jidhr
|
Raiz
|
x
|
adad mufrad
|
Números simples
|
1, 2, 3, ...
(unidades)
|
Na solução de problemas, a palavra xái (coisa) era geralmente utilizada no lugar de jidhr e as unidades eram contadas em dirhams, uma unidade monetária árabe.
Uma equação retórica aplicando todos
os números algébricos podia ser enunciada da seguinte forma:
Oito coisas e um terço de uma
coisa, menos cinco sextos de măl é igual a cem dirhams menos vinte raízes.
$$ 8\frac{1}{3}x-\frac{5}{6}x^{2}=100-20x $$
A palavra jabr
era aplicada na movimentação de uma quantidade subtraída em um lado da equação,
por exemplo:
$$ 48+3x^{2}-8x=33 $$
Movendo −8x
para o outro lado da igualdade, temos:
$$ 48+3x^{2}=33+8x $$
E o termo muqabala
combinava termos semelhantes em lados opostos da equação, por exemplo:
$$ 3\frac{1}{3}+\frac{1}{3}x=x $$
Combinando os termos em x, vem:
$$ 3\frac{1}{3}+\frac{1}{3}x-\frac{1}{3}x=x-\frac{1}{3}x $$
Chegando a:
$$ 3\frac{1}{3}=\frac{2}{3}x $$
Al-Khwarizmi classificava seus problemas algébricos em seis
categorias normalizadas e reduzidas:
Ø
Quadrados iguais a raízes. Exemplo: ax2 = bx;
Ø
Quadrados iguais a números. Exemplo: ax2 = b;
Ø
Raízes iguais a números. Exemplo: ax = b;
Ø
Quadrados e raízes iguais a números. Exemplo: ax2 + bx = c;
Ø
Quadrados e números iguais a raízes. Exemplo: ax2 + c = bx;
Ø
Quadrados iguais a raízes e números. Exemplo: ax2 = bx + c;
 |
| Página do manuscrito de álgebra “Kitab al-jabr wa l’muqabala”, escrito por Muhammad ibn Musa al-Khwarizmi, mostrando a solução de um tipo de equação quadrática pelo remate das partes de um quadrado. |
A solução para estes problemas algébricos estava
fortemente associada a conceitos geométricos, onde números e raízes eram representados
como comprimentos dos segmentos de linhas e os termos quadráticos equivaliam a
áreas. Um exemplo clássico é a solução, por al-Khwarizmi, do seguinte problema
equivalente à quarta categoria (Quadrados e raízes iguais a números. Exemplo: ax2 + bx = c ):
$$ x^{2}+10x=39 $$
Neste exemplo, o matemático começa construindo
um quadrado cujos lados valem x e
cuja área vale x.x, ou x2:
Em seguida, ele constrói retângulos, cujos
comprimentos valem x e as alturas
valem 5/2, com área igual a 5x/2, como abaixo:
Estes retângulos são anexados ao quadrado
original:
A soma destes quatro retângulos resulta no segundo termo da equação original:
$$ \frac{5x}{2}+\frac{5x}{2}+\frac{5x}{2}+\frac{5x}{2}=\frac{20x}{2}=10x $$
Finalmente, para completar o quadrado maior, al-Khwarizmi incluía em suas extremidades outros quatro quadrados pequenos:
Como a altura dos retângulos é 5/2, os quadrados anexados terão lados com esse mesmo valor e, portanto, suas áreas serão iguais a 25/4. A soma das áreas desses pequenos quadrados verdes resulta:
$$ \frac{25}{4}+\frac{25}{4}+\frac{25}{4}+\frac{25}{4}=\frac{100}{4}=25 $$
Na equação original, al-Khwarizmi soma 25 a ambos os termos:
$$ x^{2}+10x+25=39+25 $$
Lembrando que o termo à esquerda da equação é uma forma fatorada:
$$ x^{2}+10x+25=\left ( x+5 \right )^{2} $$
A equação original reduz-se a:
$$ \left ( x+5 \right )^{2}=64 $$
Tirando a raiz quadrada, vem:
$$ \sqrt{\left ( x+5 \right )^{2}}=\sqrt{64} $$
O que nos leva a:
$$ \left ( x+5 \right )=8 $$
E portanto a incógnita x vale:
$$ x+5=8\rightarrow x=8-5\rightarrow x=3 $$
Este exemplo demonstra porque al-Khwarizmi não aceitava raízes e coeficientes negativos. Trabalhando com quantidades concretas como comprimentos e áreas, era impossível criar figuras geométricas com dimensões negativas. Sem condições de lidar adequadamente com os números negativos, o matemático recusava sua existência. É importante observar neste ponto que a álgebra de al-Khwarizmi era basicamente retórica, utilizando-se da linguagem natural para ser expressa. Um bom exemplo disto pode ser observado no problema abaixo:
O
enunciado está dividido em duas partes. A primeira, em azul, é uma redução retórico-algébrica mais ou menos
auto-explicativa. A segunda parte, em vermelho, é um algoritmo de solução sem
uma correspondente explicação, bem como uma referência para uma das seis categorias de algoritmos aplicáveis à solução de equações do segundo grau
normalizadas e reduzidas, mais especificamente uma equação da quinta categoria
(Quadrados e números iguais a raízes. Exemplo: ax2 + c = bx). O problema acima e sua descrição em notação algébrica moderna, estão indicadas
a seguir:
$$ \left\{\begin{matrix}10=x+\left ( 10-x \right )\\ x\times \left ( 10-x \right )=21\end{matrix}\right. $$
$$ 10x-x^{2}=21 $$
$$ x^{2}-10x+21=0 $$
Resolvendo a equação do segundo grau segundo Báskara, temos:
Porém, Al-Khwarizmi valia-se somente da
geometria para demonstrar sua solução; retomando a equação na quinta categoria
normalizada e reduzida (quadrados e números iguais a raízes), temos:
$$ x^{2}+21=10x $$
Para resolvê-la, ele começa com um quadrado de lado igual a x, cuja área é x2:
Em seguida, desenhava um retângulo adjacente ao quadrado, com área igual a 21:
Nestas condições, o matemático afirmava que o retângulo maior, englobando o quadrado azul e o retângulo laranja, tem uma área igual a 10x; observe: a altura do retângulo laranja (que é também o lado do quadrado) vale x, e a largura do retângulo maior (que é a da largura do retângulo laranja somada ao lado do quadrado) vale 10, o que fornece uma área igual a 10x. Prosseguindo, al-Khwarizmi dividia o retângulo maior ao meio através de uma linha perpendicular à sua largura e com tamanho igual à metade da largura do retângulo maior:
Feito isso, ele completava o quadrado grande:
No pedaço deste quadrado grande que extrapola o retângulo laranja, o matemático criava um novo quadrado, indicado em verde abaixo:
Observe que sobrou um retângulo branco, adjacente ao quadrado verde. Vamos pintá-lo de vermelho:
Este retângulo vermelho tem o mesmo tamanho do retângulo laranja pequeno, que está entre o quadrado azul e o quadrado grande. Observe:
Bom, se o quadrado grande tem a metade da largura do retângulo grande (que vale 10), então seus lados valem 5 e sua área, 25. O pedaço do retângulo laranja dentro do quadrado grande, somado ao retângulo vermelho, resulta na área total do retângulo laranja, que é 21. Logo, a área do quadrado verde vale 4 e seus lados valem 2. Portanto, se a largura do retângulo grande vale 5 e a altura do retângulo vermelho vale 2 (pois tem o mesmo tamanho do quadrado verde), então a soma do lado do quadrado azul (que vale x) mais a altura do retângulo vermelho (que vale 2) tem que totalizar 5, que é a metade da largura do retângulo grande. Ou seja:
$$ x+2=5 $$
Aplicando a muqabala, temos:
$$ x+2-2=5-2 $$
$$ x=3 $$
Que é o valor da incógnita, ou xái (coisa) para os árabes, ou x para nós. A completa ausência de uma notação algébrica pode estar relacionada à natureza oral da cultura islâmica medieval. O conhecimento ainda era visto como algo a ser comunicado oralmente e recitar de memória era a base do aprendizado. Os alunos eram instruídos por seus xáiqs (professores) a memorizar um texto lendo-o em voz alta, pois “aquilo que o ouvido escuta, fica firmemente estabelecido no coração”. Os livros de álgebra, bem com os de aritmética, exibiam traços desta tradição de aprendizagem oral, com problemas começando com “se alguém lhe disser” e em geral na solução o aluno era instruído a “ter em mente” um valor intermediário. Os livros também não eram a única 'mídia' escrita: muitos livros de aritmética, incluindo aqueles de Khwarizmi, apresentavam algoritmos para serem escritos em alguma superfície apagável, entre as quais destaca-se a takht (placa de areia), uma plaqueta plana coberta de areia fina na qual as figuras eram desenhadas através de um estilo. Outra superfície apagável comum era a lawha (lousa, tabuleta), cuja superfície de argila macia podia ser raspada e reutilizada inúmeras vezes. Ambas as mídias são semelhantes ao quadro-negro e ao quadro-branco de hoje, pois são ideais para resolver problemas, mas não são adequados para gravar permanentemente um texto[1]. Entretanto, no século XII d.C. surgiu no Magrebe (região noroeste da África) e possivelmente também na Andaluzia (península Ibérica) uma notação específica para a álgebra: a primeira letra do nome da potência era posicionada acima do coeficiente, e uma letra árabe lam alongada, semelhante a um “L” invertido, servia como sinal de igual.
Observe:
O texto destacado em amarelo será ampliado para melhor visualização:
Que em notação moderna corresponde a:
$$ 5x^{2}+4x+3=2x^{2}+3x+6 $$
Revelo
a matéria primária inaparente, que os Sanchyas declaram serem produtivas do princípio
inteligente, sendo dirigidas a essa produção pelo ser consciente: pois é o
único elemento de tudo o que é aparente. Adoro o poder dominante, que os sábios
familiarizados com a natureza da alma pronunciam como sendo a causa do conhecimento,
assim explicado por uma pessoa consagrada: porque é o único elemento de tudo o
que é aparente. Eu venero essa computação inaparente, que aqueles que calculam
afirmam como sendo o meio da compreensão, sendo expostas por uma pessoa apta:
pois é o elemento único de tudo o que é aparente.
Uma vez que a aritmética da quantidade aparente [ou conhecida], que já foi proposta em um tratado anterior, se baseia na quantidade inaparente [ou desconhecida]; e uma vez que as questões a serem resolvidas dificilmente podem ser entendidas por qualquer um, e de modo algum por meio de apreensões maçantes, sem a aplicação de uma quantidade inaparente; Eis que proponho as operações de análise.[...]
Resumidamente, Báskhara demonstra sua profunda admiração pela arte do cálculo algébrico (ainda que ele não a chamasse assim) para encontrar o valor de uma incógnita e de como operá-la aplicando as regras aritméticas apresentadas por ele em um tratado anterior. Por exemplo, considere a equação abaixo:
$$ \left ( 5x-1 \right )\times \left ( 3x+2 \right ) $$
Na notação de Báskhara, a mesma expressão inicial era formulada conforme abaixo:
$$ ya\ 5\ ru\ \hat{1} $$
$$ ya\ 3\ ru\ 2 $$
Efetuando a multiplicação entre os termos, temos:
$$ \left ( 5x-1 \right )\times \left ( 3x+2 \right ) $$
$$ 15x^{2}+10x-3x-2 $$
$$ 15^{2}+7x-2 $$
A equação quadrática resultante na notação do hindu fica:
$$ ya\ v\ 15\ \ ya\ 7\ \ ru\ \hat{2} $$
A marcação acima dos números 1 e 2 na notação hindu (como um acento circunflexo) indica que eles são números negativos. Porém, Brahmagupta (598 – 668 d.C.), de quem o próprio Báskhara considerava “uma jóia entre os matemáticos”, é quem fornece as duas regras para a solução de equações quadráticas. Brahmagupta (cujo sufixo gupta sugere que sua família pertencia à casta Vaisya, composta principalmente por fazendeiros e comerciantes) teve a oportunidade de viver, estudar e ensinar em Ujjain, uma cidade no estado de Gwalior, na Índia.
Naquela época, Ujjain era o centro da matemática e
astronomia hindus e contava com o melhor observatório de toda a Índia. É também
nesse estado que se encontra o forte de
Gwalior, que possui um pequeno templo dedicado ao deus Vishnu onde, na parte interna da nave, há uma placa com a primeira
evidência indubitável do número zero, como já comentado no capítulo: Zero, o número filosofal, constante do
primeiro volume desta série. Sem dúvida que Brahmagupta não é o descobridor dessas
duas regras para a solução de equações quadráticas; mas talvez pela primeira
vez na história da álgebra encontramos o processo para solucioná-las de modo
tão claro. O original em sânscrito da primeira regra está apresentado a seguir:
Lembrando
que a equação quadrática pode ser expressa como:
$$ ax^{2}+bx+c=0 $$
Transformando
a regra de Brahmagupta em uma expressão matemática, obtemos:
$$ x=\frac{\sqrt{4ac+b^{2}}-b}{2a} $$
O matemático empregou o termo madhya (meio) para designar a incógnita x e seu respectivo coeficiente, b. O original em sânscrito da segunda regra pode ser observado a seguir:
Transformando
novamente a regra de Brahmagupta em uma expressão matemática, obtemos:
$$ x=\frac{\sqrt{ac+\left ( \frac{b}{2} \right )^{2}}-\left ( \frac{b}{2} \right )}{a} $$
A segunda regra, com um pouco de álgebra, reduz-se a:
$$ x=\frac{\sqrt{4ac+b^{2}}-b}{2a} $$
Estas expressões, obtidas a partir das duas regras, são idênticas. A fórmula que resolve qualquer equação quadrática foi obtida pela primeira vez somente em 1.585 pelo matemático holandês Simon Stevin, em sua obra L’Arithmetique; no Brasil é conhecida como fórmula de Bháskara e apresentada no formato abaixo:
$$ x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a} $$
Mas, rigorosamente falando, não foi Brahmagupta quem criou a fórmula, tampouco Bháskara, que viveu quase 600 anos depois; é um conhecimento de origem incerta, que se perde nas brumas do passado longínquo, sendo que seus rastros mais antigos encontram-se nas soluções dadas pelos babilônios.
Referências bibliográficas:
A soma destes quatro retângulos resulta no segundo termo da equação original:
$$ \frac{5x}{2}+\frac{5x}{2}+\frac{5x}{2}+\frac{5x}{2}=\frac{20x}{2}=10x $$
Finalmente, para completar o quadrado maior, al-Khwarizmi incluía em suas extremidades outros quatro quadrados pequenos:
Como a altura dos retângulos é 5/2, os quadrados anexados terão lados com esse mesmo valor e, portanto, suas áreas serão iguais a 25/4. A soma das áreas desses pequenos quadrados verdes resulta:
$$ \frac{25}{4}+\frac{25}{4}+\frac{25}{4}+\frac{25}{4}=\frac{100}{4}=25 $$
Na equação original, al-Khwarizmi soma 25 a ambos os termos:
$$ x^{2}+10x+25=39+25 $$
Lembrando que o termo à esquerda da equação é uma forma fatorada:
$$ x^{2}+10x+25=\left ( x+5 \right )^{2} $$
A equação original reduz-se a:
$$ \left ( x+5 \right )^{2}=64 $$
Tirando a raiz quadrada, vem:
$$ \sqrt{\left ( x+5 \right )^{2}}=\sqrt{64} $$
O que nos leva a:
$$ \left ( x+5 \right )=8 $$
E portanto a incógnita x vale:
$$ x+5=8\rightarrow x=8-5\rightarrow x=3 $$
Este exemplo demonstra porque al-Khwarizmi não aceitava raízes e coeficientes negativos. Trabalhando com quantidades concretas como comprimentos e áreas, era impossível criar figuras geométricas com dimensões negativas. Sem condições de lidar adequadamente com os números negativos, o matemático recusava sua existência. É importante observar neste ponto que a álgebra de al-Khwarizmi era basicamente retórica, utilizando-se da linguagem natural para ser expressa. Um bom exemplo disto pode ser observado no problema abaixo:
Dividi dez em duas partes. Em
seguida, multipliquei um deles pelo outro, e vinte e um resultaram. Então,
agora você sabe que uma das duas seções de dez é uma coisa (xái). Portanto,
multiplique-o com dez com uma coisa removida, e diga: dez com uma coisa
removida vezes uma coisa são dez coisas, com um măl (x2) removido,
que se torna igual a vinte e um. Portanto, restaure (jabr) dez coisas por um măl,
e some um măl a vinte e um, e diga: dez coisas se
tornam iguais a vinte e um e um măl. Portanto, reduza à metade as raízes
(jidhr) e elas serão cinco, que você multiplica por ele mesmo, e resultam vinte
e cinco. Destes, retire vinte e um, restando quatro. Cuja raiz você extrai, que
é dois, que você subtrai da metade das coisas. Restarão assim três, que é uma
das partes.
$$ \left\{\begin{matrix}10=x+\left ( 10-x \right )\\ x\times \left ( 10-x \right )=21\end{matrix}\right. $$
$$ 10x-x^{2}=21 $$
$$ x^{2}-10x+21=0 $$
Resolvendo a equação do segundo grau segundo Báskara, temos:
| $$ x_{1}=3 $$ |
ou
|
$$ x_{2}=7 $$ |
$$ x^{2}+21=10x $$
Para resolvê-la, ele começa com um quadrado de lado igual a x, cuja área é x2:
Em seguida, desenhava um retângulo adjacente ao quadrado, com área igual a 21:
Nestas condições, o matemático afirmava que o retângulo maior, englobando o quadrado azul e o retângulo laranja, tem uma área igual a 10x; observe: a altura do retângulo laranja (que é também o lado do quadrado) vale x, e a largura do retângulo maior (que é a da largura do retângulo laranja somada ao lado do quadrado) vale 10, o que fornece uma área igual a 10x. Prosseguindo, al-Khwarizmi dividia o retângulo maior ao meio através de uma linha perpendicular à sua largura e com tamanho igual à metade da largura do retângulo maior:
Feito isso, ele completava o quadrado grande:
No pedaço deste quadrado grande que extrapola o retângulo laranja, o matemático criava um novo quadrado, indicado em verde abaixo:
Observe que sobrou um retângulo branco, adjacente ao quadrado verde. Vamos pintá-lo de vermelho:
Este retângulo vermelho tem o mesmo tamanho do retângulo laranja pequeno, que está entre o quadrado azul e o quadrado grande. Observe:
Bom, se o quadrado grande tem a metade da largura do retângulo grande (que vale 10), então seus lados valem 5 e sua área, 25. O pedaço do retângulo laranja dentro do quadrado grande, somado ao retângulo vermelho, resulta na área total do retângulo laranja, que é 21. Logo, a área do quadrado verde vale 4 e seus lados valem 2. Portanto, se a largura do retângulo grande vale 5 e a altura do retângulo vermelho vale 2 (pois tem o mesmo tamanho do quadrado verde), então a soma do lado do quadrado azul (que vale x) mais a altura do retângulo vermelho (que vale 2) tem que totalizar 5, que é a metade da largura do retângulo grande. Ou seja:
$$ x+2=5 $$
Aplicando a muqabala, temos:
$$ x+2-2=5-2 $$
$$ x=3 $$
Que é o valor da incógnita, ou xái (coisa) para os árabes, ou x para nós. A completa ausência de uma notação algébrica pode estar relacionada à natureza oral da cultura islâmica medieval. O conhecimento ainda era visto como algo a ser comunicado oralmente e recitar de memória era a base do aprendizado. Os alunos eram instruídos por seus xáiqs (professores) a memorizar um texto lendo-o em voz alta, pois “aquilo que o ouvido escuta, fica firmemente estabelecido no coração”. Os livros de álgebra, bem com os de aritmética, exibiam traços desta tradição de aprendizagem oral, com problemas começando com “se alguém lhe disser” e em geral na solução o aluno era instruído a “ter em mente” um valor intermediário. Os livros também não eram a única 'mídia' escrita: muitos livros de aritmética, incluindo aqueles de Khwarizmi, apresentavam algoritmos para serem escritos em alguma superfície apagável, entre as quais destaca-se a takht (placa de areia), uma plaqueta plana coberta de areia fina na qual as figuras eram desenhadas através de um estilo. Outra superfície apagável comum era a lawha (lousa, tabuleta), cuja superfície de argila macia podia ser raspada e reutilizada inúmeras vezes. Ambas as mídias são semelhantes ao quadro-negro e ao quadro-branco de hoje, pois são ideais para resolver problemas, mas não são adequados para gravar permanentemente um texto[1]. Entretanto, no século XII d.C. surgiu no Magrebe (região noroeste da África) e possivelmente também na Andaluzia (península Ibérica) uma notação específica para a álgebra: a primeira letra do nome da potência era posicionada acima do coeficiente, e uma letra árabe lam alongada, semelhante a um “L” invertido, servia como sinal de igual.
[1]
Em
Portugal, nas décadas de 1930/1940, todo aluno possuía uma pequenina lousa de
ardósia, em que escreviam com giz e apagavam com um pano as lições de
matemática aplicadas pelo professor em sala de aula. O aprendizado era pautado
na memorização, uma vez que não se utilizavam cadernos para anotar os
exercícios nem as soluções dos problemas. Meu pai estudou matemática dessa
forma. Talvez por isso tenha uma memória tão boa e faça contas tão bem!
Observe:
O texto destacado em amarelo será ampliado para melhor visualização:
Traduzindo da direita para a esquerda, e utilizando a letra m para măl (a incógnita ao quadrado) e c para xái (coisa ou incógnita),
teremos:
m
|
c
|
m
|
c
|
|||
5
|
4
|
3
|
=
|
2
|
3
|
6
|
$$ 5x^{2}+4x+3=2x^{2}+3x+6 $$
Poucos livros práticos foram escritos utilizando essa
notação. Todos foram elaborados na região do Magrebe e Andaluzia (que afinal foram
regiões dominadas pelo califado Omíada, o segundo após a morte de Maomé, entre
661 e 750 d.C., sendo posteriormente suplantado pelo califado Abássida, que
durou de 750 até 1.299 d.C.) e nenhum desses manuscritos veio das mãos de
matemáticos árabes famosos como al-Khwarizmi, al-Karaji, al-Samawal, entre
outros. Outro matemático que se valeu de uma notação algébrica própria foi o
hindu Báskhara II (1.114 a 1.185 d.C.), provavelmente o principal matemático do
século XII; em seu tratado de álgebra Vija
Ganita, ele apresenta as regras aritméticas da soma, subtração, multiplicação,
divisão e raiz quadrada iniciando o texto com uma invocação muito peculiar, típica dos hindus, como se observa a seguir:
Uma vez que a aritmética da quantidade aparente [ou conhecida], que já foi proposta em um tratado anterior, se baseia na quantidade inaparente [ou desconhecida]; e uma vez que as questões a serem resolvidas dificilmente podem ser entendidas por qualquer um, e de modo algum por meio de apreensões maçantes, sem a aplicação de uma quantidade inaparente; Eis que proponho as operações de análise.[...]
Resumidamente, Báskhara demonstra sua profunda admiração pela arte do cálculo algébrico (ainda que ele não a chamasse assim) para encontrar o valor de uma incógnita e de como operá-la aplicando as regras aritméticas apresentadas por ele em um tratado anterior. Por exemplo, considere a equação abaixo:
$$ \left ( 5x-1 \right )\times \left ( 3x+2 \right ) $$
Na notação de Báskhara, a mesma expressão inicial era formulada conforme abaixo:
$$ ya\ 5\ ru\ \hat{1} $$
$$ ya\ 3\ ru\ 2 $$
Efetuando a multiplicação entre os termos, temos:
$$ \left ( 5x-1 \right )\times \left ( 3x+2 \right ) $$
$$ 15x^{2}+10x-3x-2 $$
$$ 15^{2}+7x-2 $$
A equação quadrática resultante na notação do hindu fica:
$$ ya\ v\ 15\ \ ya\ 7\ \ ru\ \hat{2} $$
A marcação acima dos números 1 e 2 na notação hindu (como um acento circunflexo) indica que eles são números negativos. Porém, Brahmagupta (598 – 668 d.C.), de quem o próprio Báskhara considerava “uma jóia entre os matemáticos”, é quem fornece as duas regras para a solução de equações quadráticas. Brahmagupta (cujo sufixo gupta sugere que sua família pertencia à casta Vaisya, composta principalmente por fazendeiros e comerciantes) teve a oportunidade de viver, estudar e ensinar em Ujjain, uma cidade no estado de Gwalior, na Índia.
 |
| Ilustração do século XIX de um hindu astrônomo. Legenda original: “Dybuck, um astrônomo, calculando um eclipse”. Ilustração de Frans Balthazar Solvyns, publicado em seu livro “Les hindous”, em 1808. |
Cuja tradução é:
O quadrático: a quantidade absoluta
multiplicada por 4, vezes o coeficiente do quadrado da incógnita, são somados
ao quadrado do coeficiente do meio (isto é, da incógnita); a raiz quadrada do
resultado, subtraído do coeficiente do meio e dividido por duas vezes o
coeficiente do quadrado da incógnita, é o valor da incógnita.
$$ ax^{2}+bx+c=0 $$
Temos que:
a → é o
coeficiente da incógnita ao quadrado;
b → é o
coeficiente do meio;
c → é a quantidade
absoluta;
$$ x=\frac{\sqrt{4ac+b^{2}}-b}{2a} $$
O matemático empregou o termo madhya (meio) para designar a incógnita x e seu respectivo coeficiente, b. O original em sânscrito da segunda regra pode ser observado a seguir:
E sua tradução é:
O termo absoluto, multiplicado pelo
coeficiente do quadrado da incógnita, é somado pelo quadrado da metade do
coeficiente da incógnita; a raiz quadrada do resultado, subtraído da metade do
coeficiente da incógnita, e dividido pelo coeficiente do quadrado da incógnita,
é o valor da incógnita.
$$ x=\frac{\sqrt{ac+\left ( \frac{b}{2} \right )^{2}}-\left ( \frac{b}{2} \right )}{a} $$
A segunda regra, com um pouco de álgebra, reduz-se a:
$$ x=\frac{\sqrt{4ac+b^{2}}-b}{2a} $$
Estas expressões, obtidas a partir das duas regras, são idênticas. A fórmula que resolve qualquer equação quadrática foi obtida pela primeira vez somente em 1.585 pelo matemático holandês Simon Stevin, em sua obra L’Arithmetique; no Brasil é conhecida como fórmula de Bháskara e apresentada no formato abaixo:
$$ x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a} $$
Mas, rigorosamente falando, não foi Brahmagupta quem criou a fórmula, tampouco Bháskara, que viveu quase 600 anos depois; é um conhecimento de origem incerta, que se perde nas brumas do passado longínquo, sendo que seus rastros mais antigos encontram-se nas soluções dadas pelos babilônios.
Referências bibliográficas:
[1]
|
Heath, T. “A history of Greek mathematics”, volumes I and II, Oxford
at the Clarendon Press, 1921.
|
[2]
|
Becker, R. L. “A algebra
geométrica de Euclides”, trabalho de conclusão de curso no curso de
matemática, Universidade Federal de Santa Catarina, 2004.
|
[3]
|
Ramos, M. D. C. P. “Da
álgebra geométrica grega à geometria analítica de Descartes e de Fermat”,
dissertação de mestrado, Faculdade de Ciências da Universidade do Porto em
Matemática, 2013.
|
[4]
|
Stillwell, J. “Mathematics and its history”, Third edition, Springer,
2010.
|
[5]
|
Radford, L.; Empey, H. “Culture, knowledge and the self: Mathematics
and the formation of new social sensibilities in the Renaissance and medieval
Islam”, Revista Brasileira de História da Matemática, Especial no 1 – Festschrift
Ubiratan D’Ambrosio, dezembro/2007.
|
[6]
|
Hettle, C. “The symbolic and mathematical influence of Diophantu’s
Arithmetica”, Journal of Humanistic Mathematics, volume5, issue 1, January
2015.
|
[7]
|
Christianidis, J. “The way of Diophantus: Some clarifications on
Diophantus’ method of solution”, Historia Mathematica 34, pgs. 289-305, 2007.
|
[8]
|
Rogers, E. “Islamic mathematics”, MATH 390: Islamic Mathematics,
Univesity of Illinois at Urbana-Champaign, August 2008.
|
[9]
|
Rashed R. (reviewed by Jeffrey Oaks) “Abu Kamil. Algèbre et analyse Diophantienne”,
Scientia Graeco-Arabica 9, Berlin/Boston: Walter de Gruyter, 2012.
|
[10]
|
Hoyrup, J. “Advanced arithmetic from twelfth-century Al-Andalus, surviving
only (and anonymously) in latin translation? A narrative that disappeared”, Contribution
to the Conference: Narratives on Translations, Max-Planck Institut für
Wissenschaftsgeschichte, Berlin, 11–20 November 2015.
|
[11]
|
Oaks, J. A.; Alkhateeb, H. M. “Simplifying equations in Arabic
algebra”, Historia Mathematica, 2006.
|
[12]
|
Awan, N. M. “Quran and mathematics – I”, Jihat al-Islam, Vol. 3, No.
1, July-December 2009.
|
[13]
|
Oaks, J. “The series of problems in al-Khwarizmi’s algebra”, class
annotations.
|
[14]
|
Colebrooke, H. T. “Arithmetic and mensuration from the sanscrit of
Brahmegupta and Bhascara”, London, John Murray, Albermale Street, 1817.
|
[15]
|
Sharma, A. R. S. “Brahma-Sphuta Siddhanta with Vasana, Vijnana -
Sanskrit and Hindi Commentaries, Vol. 1”, edited by Acharyavara Ram Swarup
Sharma, Indian Institute of Astronomical and Sanskrit Research, 1966.
|
[16]
|
Stevin, S. (Autor); Dijksterhuis, J. (Editor) “The principal works of
Michael Stevin”, C. V. Swets & Zeitlinger, 1955.
|