Lei de Newcomb-Benford como ferramenta de auditoria

Nota introdutória
Este artigo introduz o leitor aos aspectos matemáticos elementares e a um exemplo de aplicação prática da lei de Newcomb-Benford. Esta lei é aderente a diversos fenômenos de caráter financeiro, contábil, físico, entre outros. Recomenda-se fortemente a leitura de outras fontes de pesquisa para um aprofundamento dos tópicos abordados.

Lei de Newcomb-Benford como ferramenta de auditoria
A administração de uma empresa em um cenário competitivo e globalizado exige recursos, metodologia e ferramental adequados que ofereçam suporte às tomadas de decisão da alta administração de modo a preservar, legitimar e manter íntegras as atividades nela desenvolvidas [1]. Com esse objetivo em mente as empresas constituem, através de políticas internas ou por determinação legal, um setor de auditoria interna que sustente a alta administração com informações e sugestões que auxiliem e dêem suporte às atividades pelas quais são responsáveis [2]. E dentro desse contexto, o auditor interno tem que transmitir uma posição de igualdade e justiça quando aborda assuntos muitas vezes sensíveis e até controversos, transmitindo confiança e responsabilidade na apuração e geração de informações fidedignas [3].

Nenhuma empresa, seja qual for a esfera ou porte, estará imune a fraudes ou falhas de segurança em seus processos, mesmo aquelas organizações que aderiram à Lei Sarbanes-Oxley (SOX). A SOX obriga a criação de mecanismos de controle que fortaleçam as regras de governança corporativa, melhorando a transparência dos mecanismos de gestão [4]. Nesse sentido, a lei de Newcomb-Benford transforma-se numa interessante ferramenta auxiliar na detecção de indícios de: faturamentos irregulares; alterações, desvios ou furtos nos estoques; pagamentos indevidos ou fictícios; inconsistências em demonstrações econômico-financeiras; lançamentos contábeis inconsistentes. 

Exemplos de aplicações da Lei de Newcomb-Benford na auditoria 

Credita-se a Carslaw [5] a primeira aplicação contábil da lei de Newcomb-Benford. Em seu artigo, ele afirma que quando as receitas líquidas corporativas encontram-se ligeiramente abaixo de um ‘limite psicológico’, os gerentes tenderiam a arredondá-las para cima, de modo que os primeiros números parecessem maiores, ainda que fossem apenas marginalmente maiores em termos percentuais. Seus resultados mostraram que havia mais 0s e menos 9s no segundo dígito que o esperado, o que sugere que houve arredondamentos nos dados coletados.

Já Nigrini e Mittermaier [6] utilizaram a base matemática da lei de Newcomb-Benford para testes numéricos a serem aplicados pelos auditores como procedimentos analíticos nos estágios de planejamento da auditoria, testando a autenticidade de listas numéricas pela comparação das freqüências reais e esperadas dos primeiros dígitos em uma companhia de petróleo. Seus resultados mostraram a validade da lei quando aplicados testes de análise digital no primeiro e segundo dígitos, na duplicação de números e nos arredondamentos, entre outros.

Por sua vez, Durtschi, Hillison e Pucini [7] afirmam que, apesar da lei de Newcomb-Benford ser uma ferramenta simples e efetiva na detecção de fraudes, o auditor deve estar atento aos conjuntos de dados aos quais essa lei é aplicável, como por exemplo: contas a pagar e a receber, desembolsos, vendas e despesas, balanços anuais entre outros conjuntos de números contábeis. Analisam também o poder dos testes estatísticos para determinar em que ponto da análise um desvio pode ser considerado grande o suficiente para ser uma indicação significativa de fraude e apontam o uso da distribuição qui-quadrática e da estatística Z para a determinação desses limites. Concluem que a lei de Newcomb-Benford, quando utilizada corretamente, é uma ferramenta útil na identificação de contas suspeitas para posterior análise.

Já Lu e Boritz [8] analisaram conjuntos de dados incompletos e argumentam que o problema entre esses conjuntos de dados e a lei de Newcomb-Benford tradicional é que as freqüências dos dígitos observados tornam-se inflacionados quando computados como uma probabilidade e propõem um algoritmo em que definem um fator de escalonamento a ser utilizado para preencher os dados faltantes da distribuição de freqüências dos primeiros dígitos. Com esse algoritmo, os autores tentaram detectar anomalias que pudessem ser indicativas de atividade fraudulenta em um conjunto incompleto de dados de reembolsos financeiros do plano de saúde de uma empresa, no período de 2003 a 2005. Segundo afirmam, o algoritmo seria mais preciso ao reportar uma seqüência menor de dígitos anômalos que a lei de Newcomb-Benford tradicional, tendo-se utilizado um nível de confiança de 95% como limiar da existência de anomalias.

No Brasil, os artigos técnicos relacionados ao tema estão basicamente centralizados na análise de contas públicas nas esferas municipal, estadual e federal. Dos Santos, Diniz e Corrar [9] evidenciam o modelo contabilométrico fundamentando-o na relação entre a lei de Newcomb-Benford e os testes de hipóteses (estatística Z e a distribuição qui-quadrática) envolvendo 20 municípios da Paraíba e utilizando-se um total de 104 mil notas de empenho. Concluem pela existência de fortes indícios de superfaturamento e fracionamento de despesas para burlar os limites estabelecidos pela Lei 8.666, das licitações.

Por seu lado, Lagioia e outros [10] verificaram a aplicabilidade da auditoria digital em empresas prestadoras de serviços em um município do nordeste brasileiro, a fim de identificar a sinalização de desvios em notas fiscais paralelas, calçadas e não escrituradas. Concluem que a lei de Newcomb-Benford é aplicável à fiscalização do imposto sobre serviços e salientam a urgência de se alterarem as formas e regras para se auditarem as empresas bem como a divulgação desses resultados aos demais municípios por não exigir novos investimentos em sua implantação.

Por fim, Costa, Dos Santos e Travassos [11] aplicam a lei de Newcomb-Benford na análise de mais de 134 mil notas de empenho emitidas por vinte unidades gestoras de dois estados da União. O estudo indica excesso de ocorrências no primeiro dígito para notas de empenho iniciadas por 7 e 8 e escassez de ocorrências para notas de empenho iniciadas por 6 e 9, sugerindo um comportamento de fuga à realização de processos licitatórios nos gastos públicos. Observam também que, quanto ao segundo dígito, os maiores desvios em excesso ocorrem para os dígitos 0 e 5, indicando arredondamentos nos valores dos empenhos, sugerindo que estes não estejam sendo formados pela aplicação direta de uma margem de lucro ao montante dos seus custos e despesas para produzir e vender.

A origem da lei de Newcomb-Benford 

A lei de Newcomb-Benford estabelece empiricamente que em determinadas fontes de dados o primeiro dígito não apresenta uma distribuição uniforme de ocorrências dos algarismos de 1 a 9, mas antes uma distribuição logarítmica decrescente quanto maior for o algarismo. Este tipo de distribuição ocorre para uma ampla gama de conjuntos de dados: número do endereço residencial, população por cidade, taxas de mortalidade, bem como constantes físicas e matemáticas. Por outro lado, o conjunto amostral relativo à altura de adultos em uma cidade, por exemplo, não é aderente à lei.

Simon Newcomb, astrônomo e matemático canadense, foi o primeiro a identificar este princípio estatístico, ou pelo menos a reportá-lo formalmente em seu artigo de 1881, onde afirma: “Que os dez dígitos não ocorrem com igual freqüência está evidente a qualquer um que faça muito uso de tabelas logarítmicas e nota quão rapidamente as primeiras páginas desgastam-se em relação às últimas. O primeiro número significativo é comumente o 1 mais que qualquer outro, e a freqüência diminui até 9” [12]. Porém, coube a Frank Benford, engenheiro eletricista e físico norte-americano, redescobrir e generalizar este princípio em seu artigo de 1938, dando-lhe a formatação matemática conhecida atualmente.

Equacionamento da lei de Newcomb-Benford 

Supondo que exista uma distribuição de probabilidades P(x) que englobe o espaço amostral caracterizado pelos dígitos escalares de 1 a 9, então essa distribuição deve ser invariante sob uma mudança de escala k [13][14], ou seja:

$$ P\left ( kx \right )=f\left ( k \right )P\left ( x \right ) $$

(1)

Definindo ainda que a área sob a curva da distribuição de probabilidades seja normalizada e igual a um, vem:

$$ \int P\left ( x \right )dx=1 $$

Temos por igualdade que:

$$ \int P\left ( kx \right )dx=\int f\left ( k \right )P\left ( x \right )dx $$

Pelo método da substituição, vem:

$$ u=kx $$

$$ \frac{du}{dx}=k\rightarrow dx=\frac{du}{k} $$

E assim:

$$ \frac{1}{k}\int P\left ( u \right )du=f\left ( k \right )\int P\left ( x \right )dx $$

Donde se conclui que a função que define a mudança de escala é dada por:

$$ f\left ( k \right )=\frac{1}{k} $$

Diferenciando agora a equação (1) em relação a k, vem:

$$ \dot{P}\left ( kx \right )=P\left ( x \right )\dot{f}\left ( k \right ) $$

$$ \dot{P}\left ( kx \right )x+P\left ( kx \right )\dot{x}=P\left ( x \right )\dot{f}\left ( k \right ) $$

$$ \dot{P}\left ( kx \right )x=P\left ( x \right )\dot{f}\left ( k \right ) $$

E para f(k) = 1/k e k = 1, tem-se:

$$ \dot{P}\left (  x \right )x=P\left ( x \right )\left ( \frac{-1}{k^{2}} \right ) $$

$$ x\dot{P}\left ( x \right )=-P\left ( x \right ) $$

(2)

Finalmente, integrando a diferencial da equação (2), vem:

$$ x\dot{P}\left ( x \right )dx=-P\left ( x \right )dx $$

$$ \frac{\dot{P}\left ( x \right )}{P\left ( x \right )}dx=\frac{-1}{x}dx $$

$$ \int_{1}^{x}\frac{\dot{P}\left ( x \right )}{P\left ( x \right )}dx=\int_{1}^{x}\frac{-1}{x}dx $$

$$ ln\left [ P\left ( x \right ) \right ]=ln\left ( x^{-1} \right ) $$

$$ P\left ( x \right )=\frac{1}{x} $$

(3)

Observa-se facilmente pela equação (3) que a área sob a curva da densidade de probabilidades P(x) é logarítmica para:

$$ x\in \left \{ 1 ...9 \right \} $$

De fato, uma escala logarítmica não distribui uniformemente o espaço amostral em questão, como se pode observar na figura 1:

Figura 1 – Distribuição logarítmica dos algarismos de 1 a 9

Assim, pode-se afirmar que a probabilidade de que uma constante qualquer comece com o dígito d é proporcional ao comprimento desse dígito na escala logarítmica, ou seja:

$$ P\left ( d\leq x\leq d+1 \right )=\frac{\int_{d}^{d+1}P\left ( x \right )dx}{\int_{1}^{10}P\left ( x \right )dx} $$

$$ P\left ( d\leq x\leq d+1 \right )=\frac{ln\left ( d+1 \right )-ln\left ( d \right )}{ln\left ( 10 \right )-ln\left ( 1 \right )}=\frac{ln\left ( 1+\frac{1}{d} \right )}{ln\left ( 10 \right )} $$

Ou, genericamente:

$$ P\left ( d \right )=log_{10}\left ( 1+\frac{1}{d} \right ) $$

(4)

A equação (4) matematiza a lei de Newcomb-Benford e descreve a probabilidade de ocorrência de qualquer primeiro dígito para determinados conjuntos de dados numéricos, cujas proporções estão indicadas na tabela 1.

Tabela 1 – Probabilidade de ocorrência do primeiro dígito, segundo a lei de Newcomb-Benford

Testes de hipótese e a lei de Newcomb-Benford

Uma hipótese estatística é uma afirmação que confirma ou nega uma suposição formulada em relação aos parâmetros de uma ou mais populações (testes paramétricos) ou em relação à distribuição da população (testes de ajustamento). A metodologia de construção de um teste de hipótese parte da fixação do nível de significância ou confiança α (que é usado para decidir se a diferença amostral obtida é estatisticamente significante) e dos graus de liberdade n (ou seja, a quantidade de variáveis livres que serão utilizadas para o cálculo estatístico).

Para este estudo, dois testes de hipótese serão aplicados: estatística Z e a distribuição Qui-quadrática. A estatística Z é um teste estatístico utilizado para determinar se duas médias de população são diferentes quando as variâncias são conhecidas e o tamanho da amostra é grande, e cuja fórmula é dada por [9]:

$$ Z=\frac{\left | p_{o}-p_{e} \right |-\frac{1}{2n}}{\sqrt{\frac{p_{e}\left ( 1-p_{e} \right )}{n}}}x $$

(5)

Onde n é o número de observações, p_o é a probabilidade obtida para os eventos em análise e p_e é a probabilidade esperada segundo a lei de Newcomb-Benford. O termo 1/2n só é aplicado se for menor que | p_o - p_e|. E a distribuição Qui-quadrática será utilizada para encontrar um valor de dispersão entre duas variáveis, avaliando a existência ou não de algum tipo de associação ou dependência entre ambas. Sua fórmula é dada por [9]:

$$ \chi ^{2}=\sum_{d=1}^{9}\frac{\left ( P_{o}-P_{e} \right )}{P_{e}} $$

(6)

Onde n é o número de observações, P_o são as proporções obtidas (definidas como p_o.n) e P_e são as proporções esperadas (definidas como p_e.n). Os testes de hipótese enfim serão utilizados para corroborar estatisticamente os números obtidos com aqueles esperados pela lei de Newcomb-Benford, oferecendo uma metodologia conhecida que dê respaldo aos resultados encontrados.

Aplicação da lei de Newcomb-Benford em números de endereços

A título de constatação da lei de Newcomb-Benford e da validade dos resultados obtidos a partir dos testes de hipótese, será apresentada nos próximos sub-tópicos a densidade de probabilidades para números de endereços de três municípios do Estado de São Paulo. As amostras foram obtidas após levantamento e mineração de dados comerciais.

Densidade de probabilidades para números de endereços

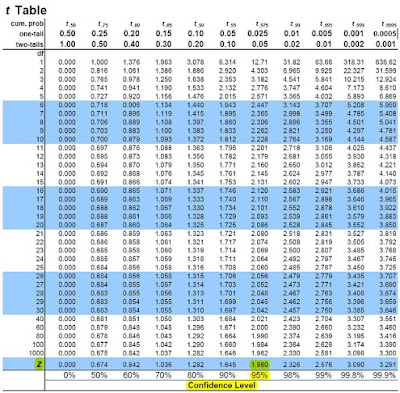
Para esta análise será utilizado um nível de significância  de 5% (ou, dito de outra forma, um nível de confiança de 95%), que corresponde a um valor crítico para Z de 1,960 (vide tabela T-student abaixo, no Anexo B, com os valores destacados em amarelo). E para este nível de significância, com 8 graus de liberdade ([9 – 1] dígitos), o valor crítico para χ² será de 15,507 (vide tabela Qui-quadrado no Anexo A com os valores destacados em amarelo).

Município de São José dos Campos

O gráfico da figura 2 apresenta as probabilidades obtidas após a extração do primeiro dígito do número de endereço dos 191.102 imóveis cadastrados nesse município.

Figura 2 – Densidade de probabilidades do primeiro dígito do número de endereço dos imóveis do município de São José dos Campos

E a tabela 2 apresenta as probabilidades e proporções obtidas e esperadas, bem como os respectivos testes de hipótese para o primeiro dígito do número dos endereços dos imóveis de São José dos Campos:

Tabela 2 – Probabilidades e proporções obtidas e esperadas e respectivos testes de hipótese para o primeiro dígito do número dos endereços dos imóveis do município de São José dos Campos

Observa-se para este exemplo uma grande convergência entre as probabilidades obtidas e aquelas esperadas pela lei de Newcomb-Benford, corroborando a informação do gráfico da figura 2. Note que na coluna da estatística Z não há nenhum valor acima do crítico de 1,960 e na coluna do Qui-Quadrado a somatória de 2,2583 está muito abaixo do valor crítico de 15,507.

Município de Presidente Prudente

O gráfico da figura 3 apresenta os resultados obtidos após a extração do primeiro dígito do número de endereço dos 82.212 imóveis cadastrados.

Figura 3 – Densidade de probabilidades do primeiro dígito do número de endereço dos imóveis do município de Presidente Prudente

E a tabela 3 apresenta as probabilidades e proporções obtidas e esperadas, bem como os respectivos testes de hipótese para o primeiro dígito do número dos endereços das ligações de água de Presidente Prudente:

Tabela 3 – Probabilidades e proporções obtidas e esperadas e respectivos testes de hipótese para o primeiro dígito do número dos endereços dos imóveis do município de Presidente Prudente

Observa-se para este exemplo uma convergência razoável entre as probabilidades obtidas e aquelas esperadas pela lei de Newcomb-Benford, concordante com a informação do gráfico da figura 3. Note que na coluna da estatística Z há apenas um valor (para o dígito 2) ligeiramente acima do crítico de 1,960 e na coluna do Qui-Quadrado a somatória de 15,2675 está muito próximo do valor crítico de 15,507, mas ainda abaixo.

Município de Mongaguá

O gráfico da figura 4 apresenta os resultados obtidos após a extração do primeiro dígito do número de endereço dos 37.626 imóveis cadastrados.

Figura 4 – Densidade de probabilidades do primeiro dígito do número de endereço dos imóveis do município de Mongaguá

E a tabela 4 apresenta as probabilidades e proporções obtidas e esperadas, bem como os respectivos testes de hipótese para o primeiro dígito do número dos endereços dos imóveis de Mongaguá:

Tabela 4 – Probabilidades e proporções obtidas e esperadas e respectivos testes de hipótese para o primeiro dígito do número dos endereços dos imóveis do município de Mongaguá

Observa-se para este exemplo uma não convergência entre as probabilidades obtidas e aquelas esperadas pela lei de Newcomb-Benford, concordante com a informação do gráfico da figura 4. Note que na coluna da estatística Z há apenas um valor (para o dígito 4) abaixo do crítico de 1,960 e na coluna do Qui-Quadrado a somatória de 209,1152 está muito acima do valor crítico de 15,507.

Considerações Finais

Da análise feita para os números residenciais dos três municípios em questão, observa-se que a metodologia utilizada por São José dos Campos para a numeração dos seus imóveis é eficaz, organizada e muito bem controlada. No caso de Presidente Prudente, constata-se que a incidência do primeiro dígito na numeração dos seus imóveis é, no geral, boa e convergente com as previsões. Finalmente, para o caso de Monguaguá, as discrepâncias entre as incidências do primeiro dígito dos números dos imóveis e a previsão da lei de Newcomb-Benford podem apontar para duas possíveis causas: uma é um cadastro de imóveis desatualizado ou não tão bem organizado como o existente nos outros dois municípios analisados; a outra causa pode ser uma grande quantidade de áreas invadidas ou irregulares dentro do município. Como nessas áreas a presença do Estado não se faz tão presente, a numeração dos imóveis segue, em geral, o gosto do proprietário. Uma vez que os números dos imóveis são definidos aleatoriamente, acabam por não obedecer ao comportamento logarítmico da lei de Newcomb-Benford, e essa aleatoriedade manifesta-se nos resultados estatísticos. Observa-se com este simples exemplo o potencial do uso dessa ferramenta estatística na detecção de indícios de algum tipo de irregularidade, cabendo ao auditor a análise, o rastreamento e o aprofundamento de suas pesquisas antes de chegar a um veredito.

Anexo A - Tabela Qui-quadrado

Clique na imagem para ampliá-la.

Anexo b - Tabela t-student

Clique na imagem para ampliá-la..

Dica técnica de informática
Suponha que você possua um SGBD (Sistema Gerenciador de Banco de Dados) com uma tabela denominada MUNICIPIO com duas colunas: uma contendo o código dos municípios estudados, que chamaremos de CD_MUNICIPIO, e outra coluna contendo os números dos endereços dos imóveis, que chamaremos de NR_IMOVEL, do tipo INT(10). Um possível script SQL (padrão ANSI 92) a ser utilizado para a obtenção do primeiro dígito do número dos endereços dos imóveis está indicado a seguir:

select substr(cast((nr_imovel(format 'zzzzzzzzzz')) as char(10)),1,1) as digito, count(digito)
from municipio where cd_municipio = 100 and digito in ('1', '2', '3', '4', '5', '6', '7', '8', '9') group by 1, order by 1;

Note que, talvez, a parte mais trabalhosa seja justamente o levantamento dos municípios e respectivos números de imóveis e seu armazenamento em um SGBD, e não a aplicação da lei de Newcomb-Benford, que é bastante direta já que basta dividir a quantidade de ocorrências de cada dígito pela quantidade total de imóveis. A proporção obtida em cada caso deve ser igual, ou muito próxima, à proporção prescrita pela lei.

Referências Bibliográficas

[1] Stringher R. A., “A importância da auditoria interna para gestão”, Revista Gestão de Riscos, págs. 34-36, edição 67 – Junho/2011.

[2] Nunes B. e Hulse W. H., “Análise da atividade desempenhada pelo controle interno do Tribunal de Justiça de Santa Catarina: orientação e fiscalização de recolhimentos de valores devidos ao fundo de reaparelhamento da Justiça”, Tópicos destacados na gestão do Judiciário Catarinense – vol. 1, págs. 95-123, Junho/2012.

[3] “O Auditor”, Senac – Boletim Fiscal, ano 2 – No. 8, Julho/Agosto de 2003.

[4] De Oliveira J. C. R. et alii, “O papel do controle interno na prevenção de erros e fraudes: um estudo de caso em cooperativa de crédito de Minas Gerais”, 8º Congresso USP de Iniciação Científica em Contabilidade, Julho/2011.

[5] Carslaw C., “Anomalies in income numbers: Evidence of goal oriented behavior”, The Accounting Review, págs. 321-327, Abril/1988.

[6] Nigrini M. J. e Mittermaier L. J., “The use of Benford’s law as an aid in analytical procedures”, Auditing – A Journal of Practice & Theory, vol. 16, No. 2, págs. 52-67, 1997.

[7] Durtschi C., Hillison W., Pacini C., “The effective use of Benford’s law to assist in detecting fraud in accounting data”, Journal of Forensic Accounting, vol. 5, págs. 17-34, 2004.

[8] Lu F. e Boritz J. E., “Detecting fraud in health insurance data: learning to model incomplete Benford’s law distributions”, Lecture Notes in Computer Science, vol. 3720, págs. 633-640, 2005.

[9] Santos J. et alii, “O foco é a teoria amostral nos campos da auditoria contábil tradicional e da auditoria digital: testando a lei de Newcomb-Benford para o primeiro dígito nas contas públicas”, Brazilian Business Review, vol. 2 No. 1, págs. 71-89, Junho/2005.

[10] Lagioia U. C. T. et alli, “Aplicabilidade da lei de Newcomb-Benford nas fiscalizações do imposto sobre serviços – ISS”, Revista Contabilidade & Finanças, vol. 22, No. 56, págs. 203-224, Agosto/2011.

[11] Costa J. I. de F., Dos Santos J., Travassos S. K. de M., “Análise de conformidade nos gastos públicos dos entes federativos: estudo de caso de uma aplicação da lei de Newcomb-Benford para o primeiro e segundo dígito em dois estados brasileiros”, 11º Congresso USP de Controladoria e Contabilidade, Julho/2011.

[12] Newcomb S., “Note on the frequency of use of the different digits in natural numbers”, American Journal of Mathematics, vol. 4 – No. 1, págs. 39-40, 1881.

[13] Pinkham R. S., "On the Distribution of First Significant Digits", Annals of Mathematical Statistics, No. 32, págs. 1223-1230, 1961.
[14] Benford F., "The Law of Anomalous Numbers", Proceedings of the American Philosophical Society, Vol. 78, No. 4, pp. 551-572, 1938.

Biografias curtas

Frank Albert Benford Jr. (1883 – 1948) foi um engenheiro eletricista e físico estadunidense mais conhecido por redescobrir e generalizar a lei de Benford. Também é conhecido por ter concebido, em 1937, um instrumento para medição do índice de refração do vidro. Especialista em medições óticas, publicou 109 artigos nos campos da ótica e da matemática e obteve a concessão de 20 patentes em dispositivos óticos. Trabalhou na General Electric, primeiro no laboratório de engenharia de iluminação por 18 anos e depois no laboratório de pesquisas por mais 20 anos.

Simon Newcomb (1835 – 1909) foi um astrônomo e matemático canadense. Em 1878 iniciou o planejamento de uma nova e precisa medição da velocidade da luz, que era necessária para calcular os valores exatos de muitas constantes astronômicas. Em 1881 descobriu o princípio estatístico mais conhecido como lei de Benford. Escreveu sobre economia e livros de ciência popular e seu nome é citado no famoso conto de ficção científica de H. G. Wells: A Máquina do Tempo.

Nota Final

O texto aqui reproduzido faz parte do primeiro capítulo de minha monografia para a conclusão de um MBA em Gestão de Negócios, finalizada em 2014 na BSP - Business School São Paulo. Caso haja interesse na obtenção de uma cópia em PDF da monografia completa, clique aqui. Um exemplo bastante simples de aplicação desta lei, que inclusive pode ser aproveitada em sala de aula para turmas que estejam aprendendo logaritmos, pode ser encontrada neste breve artigo: Bancando o detetive com a lei de Newcomb-Benford.