Teano de Crotona pode ser considerada a primeira mulher matemática do mundo antigo de que se tem notícia. Nascida na Grécia no século VI a.C., pouco se sabe sobre a vida desta mulher e as fontes antigas que lhe fazem referência são confusas. Segundo uma das tradições, ela teria vindo de Creta e foi filha de Pitonax de Creta (físico e filósofo do orfismo[1]); para outra tradição, acredita-se que Teano fosse de Crotona e tenha sido filha de Brontino (sucessor de Pitágoras) ou talvez filha de Pitágoras e mulher de Brontino.
[1] Orfismo (grego antigo: Ὀρφικά) é um conjunto de crenças e práticas religiosas originário das
civilizações grega e trácia, associado com a literatura atribuída ao poeta
mítico Orfeu. Os órficos reverenciavam Dioniso (que desceu uma vez ao mundo
inferior e voltou) e Perséfone (que anualmente descia ao Mundo Inferior por uma
temporada e depois retornava, personificando a primavera). O foco central do
orfismo é o sofrimento e a morte do deus Dioniso nas mãos dos Titãs, o que
constitui a base do mito central do orfismo. De acordo com esse mito, o infante
Dioniso é morto, dilacerado e consumido pelos Titãs. Em retaliação, Zeus atinge
os Titãs com um raio, transformando-os em cinzas. Destas cinzas nasce a
humanidade. Na crença órfica, esse mito descreve a humanidade como tendo uma
natureza dual: corpo (sōma), herdado
dos Titãs, e uma centelha divina ou alma (psychē),
herdada de Dioniso. Para alcançar a salvação da existência material, titânica,
era preciso ser iniciado nos mistérios dionisíacos e passar por teletē, um ritual de purificação e
revivência do sofrimento e morte do deus. Os órficos acreditavam que, após a
morte, passariam a eternidade ao lado de Orfeu e outros heróis. Os não
iniciados (amyetri), eles
acreditavam, seriam reencarnados indefinidamente. Fonte: Wikipedia - https://pt.wikipedia.org/wiki/Orfismo_(culto)
 |
| Mosaicos de Orfeu, como ao lado, foram encontrados nas ruínas de muitas moradias romanas. Ele veste um barrete frígio e está cercado de animais encantados pelo tocar de sua lira |
Mas a tradição mais aceita diz que Teano foi uma grande
discípula de Pitágoras e também sua esposa, com quem tiveram três filhas: Damo,
Myia e Arignote, e um filho: Telauges e que ela, e duas de suas filhas,
continuaram na Escola Pitágorica após a morte de Pitágoras. Teano teria escrito
sobre matemática, física, medicina e psicologia infantil. Historiadores modernos
supõem que o trabalho mais importante por ela deixado relaciona-se ao princípio
filosófico da razão áurea ou doutrina do meio-termo[2].
Dentro da tradição pitagórica, Teano considerava que tudo que existe pode ser distinto
numericamente. O número seria o princípio da realidade e da individualidade. De
acordo com alguns pesquisadores, Teano teria afirmado na obra “Êutifron (Sobre
a Piedade)” que:
Notei que muitos dos gregos acreditam que Pitágoras
disse que todas as coisas são geradas a partir do número. A própria afirmação
impõe uma dificuldade: como coisas que não existem podem ser concebidas a
gerar? Mas ele não disse que todas as coisas vêm do número; antes, que estão de
acordo com o número – baseando-se no fato de que a ordem no sentido primário
está no número e é pela participação na ordem que um primeiro, e um segundo e o
resto são sequencialmente atribuídos a coisas que são contadas.
[2] Aparecendo no pensamento grego tão cedo quanto a Máxima
Délfica (“nada em excesso”) e enfatizada mais tarde na filosofia aristotélica,
a razão áurea, média de ouro ou doutrina do meio-termo é o meio desejável entre
dois extremos: um de excesso e outro de deficiência. Para a mentalidade grega, a
razão áurea era um atributo da beleza. Os gregos antigos acreditavam que existe
uma estreita associação em matemática entre beleza e verdade, havendo três “ingredientes”
para que a beleza se manifeste: simetria, proporção e harmonia. A beleza era um
objeto de amor e algo que deveria ser imitado e reproduzido em suas vidas, na arquitetura,
na educação (paideia) e na política. Julgavam
a vida por essa mentalidade. Fonte: Wikipedia (https://pt.wikipedia.org/wiki/Doutrina_do_meio-termo)
 |
| A antiga biblioteca de Alexandria, obra de O. Von Coven, século 19 d.C. |
 |
| Cleópatra e Otaviano, tela de Guercino, 1.630 – 1.649 |
 |
| Hipátia, gravura de Elbert Hubbard, 1908 |
[1] À Filósofa,
Estou tão mal afortunado que necessito de um densímetro. Cuide para que seja moldado em latão e montado para mim.
[2] O instrumento em questão é um tubo cilíndrico,
que tem a forma de uma flauta e possui aproximadamente o mesmo tamanho. Possui
entalhes em uma linha perpendicular, por meio dos quais podemos testar o peso
das águas. Um cone forma uma tampa em uma das extremidades, bem ajustada ao
tubo. O cone e o tubo possuem apenas uma base. Esta é chamada de barílio.
Sempre que colocares o tubo em um líquido, ele permanecerá ereto. Podes então
contar os entalhes à vontade e, desta forma, determinares a gravidade
específica da água.
 |
| Um densímetro |
“Havia em Alexandria uma mulher chamada Hipátia, filha do filósofo Téon, que fez tantas realizações em literatura e ciência que ultrapassou todos os filósofos da época. Tendo progredido na escola de Platão e Plotino, ela explicava os princípios da filosofia a quem a ouvisse, e muitos vinham de longe receber os ensinamentos. Com um grande auto-controle e descontração, que obteve como consequência do cultivo da sua mente, não raras vezes aparecia em público, na presença dos magistrados. Nem se coibia de comparecer numa assembléia de homens. Pois todos os homens a admiravam ainda mais devido à sua extraordinária dignidade e virtude. Mas até ela foi vítima da inveja política que ao tempo prevalecia. Ao manter diálogos frequentes com Orestes, foi caluniosamente relatado entre a população cristã que era ela quem impedia Orestes de se reconciliar com o bispo [Cirilo]. Por causa do zelo fanático de alguns deles, liderados por Pedro, o leitor, Hipátia foi arrancada da sua carruagem, quando voltava para casa, e foi arrastada até a igreja chamada Caesareum, onde lhe rasgaram as roupas e a mataram com ostras e pedaços de cerâmica. Depois de terem desmembrado o seu corpo, levaram os membros mutilados para um local chamado Cinaron e os queimaram. Este assunto trouxe não pequeno opróbrio quer a Cirilo, quer a toda a Igreja Alexandrina. E certamente que nada poderá estar mais distante do espírito do Cristianismo que a permissão de massacres, lutas e acontecimentos de tal ordem. Isto aconteceu no mês de Março, durante a Quaresma, no quarto ano do episcopado de Cirilo, sob o décimo consulado de Honório e o sexto de Teodósio.”
A morte de Hipátia seria “vingada” somente no século 16 d.C., quando o pintor Rafael executou um afresco para ornamentar o Palácio Apostólico, no Vaticano, a pedido do então Papa Júlio II, na obra conhecida como “Escola de Atenas”. No projeto original, Rafael posicionou Hipátia no centro do painel, abaixo de Platão e Aristóteles.
 |
| Escola de Atenas, afresco de Rafael (1509 – 1510), Palácio Apostólico, Vaticano |
 |
| Hipátia em destaque no afresco "Escola de Atenas" |
No auge da Idade Média, podem-se apontar duas mulheres que se destacaram, não na matemática, mas antes nas artes literárias: a abadessa Rosvita de Gandersheim (~935 d.C. a 973 d.C.), considerada a primeira poetisa em língua alemã, e a filósofa e escritora francesa, a freira Heloísa d’Argenteuil (~1100 d.C. a 1163/1164 d.C.). As fascinantes histórias, bem como as obras dessas duas mulheres, merecerão do estimado leitor uma cuidadosa pesquisa à parte.
 |
| Retrato de Elena Piscopia, autor desconhecido. Biblioteca Ambrosiana, Milão. |
 |
| Selo italiano em homenagem a Elena Piscopia |
 |
| A matemática Émilie du Châtelet, obra de Marianne Loir. Museu de Belas Artes de Bordeaux. |
 |
| Selo francês em homenagem a Émilie du Châtelet |
[3] John Locke foi um filósofo inglês, considerado o principal
representante do empirismo (do grego empeiria
= experiência) e um dos principais teóricos do contrato social – uma classe de
teorias que tentam explicar os caminhos que levam as pessoas a formarem Estados
e/ou manterem a ordem social. Como filósofo, pregou a teoria da tábula rasa, segundo a qual a mente
humana era como uma folha em branco, que se preenchia apenas com a experiência e
as sensações, que poderiam ser tanto externas quanto internas, caso das
reflexões e das sensações individuais. Para Locke, as reflexões acontecem no
momento em que as sensações são trabalhadas e desenvolvidas pela dúvida,
conhecimento anterior sobre fatos e objetos ou até mesmo pela crença individual
ou coletiva em algo. A junção desses elementos permite o processamento e a
classificação das diversas sensações. Essa teoria é uma crítica à doutrina das idéias inatas de Platão, segundo a qual
nascemos com princípios racionais e conteúdos mentais cujas origens viriam do
mundo inteligível ou das idéias, pelo qual passaríamos antes de nascer. Desse
modo, ao nascermos neste mundo, denominado por Platão como mundo sensível ou
das formas, tais idéias já estariam formuladas em nossas mentes, porém submersas,
e para serem devidamente utilizadas, ou relembradas, bastariam emergir. O
pensamento de John Locke influenciou vários pensadores empiristas, tais como:
David Hume, Kant, Adam Smith e o próprio Voltaire, companheiro de Émilie du
Châtelet. Fontes consultadas:
·
https://pt.wikipedia.org/wiki/John_Locke
 |
| A matemática italiana Maria Gaetana Agnesi, autor desconhecido |
 |
| Selo italiano em homenagem a Maria Gaetana Agnesi |
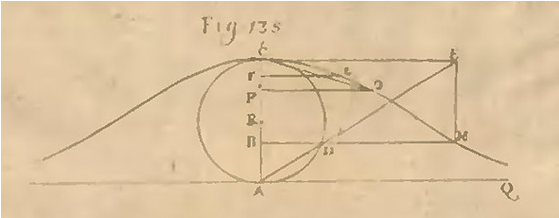 |
| A curva matemática mais famosa de Maria Gaetana Agnesi: a bruxa de Agnesi |
Seguindo as pegadas dessas mulheres incríveis, veremos agora a história da alemã Caroline Lucretia Herschel (1750 – 1848): nascida em Hanover, em uma família de músicos, foi a oitava criança e a quarta filha do casal Issak Herschel e Anna Ilse Moritzen. Logo aos cinco anos ficou incumbida de muitas tarefas domésticas depois que sua irmã Sophia, única mulher sobrevivente além dela entre as irmãs, e dezesseis anos mais velha, veio a casar-se. Aos dez anos Caroline contraiu tifo, que lhe atrofiou o crescimento, cuja altura na fase adulta não ultrapassaria 1,30 metro, além da perda de visão de seu olho esquerdo. A família, por conta de sua doença, presumiu que Caroline nunca viria a se casar, e sua mãe avaliou que o melhor para a filha seria treiná-la para se tornar governanta, ao invés de receber uma educação mais erudita, conforme os desejos de seu pai. Devido à discordância do casal, Issak aproveitava-se das ausências de Anna para ensinar diretamente sua filha, incluindo-a nas lições que ministrava aos filhos. Após a morte do pai, seu irmão William convidou-a a juntar-se a ele em Bath, na Inglaterra, onde se estabeleceria como organista e professor de música.
 |
| Selo da Guiana em homenagem a Caroline Herschel |
 |
| Caroline e William Herschel, litografia a cores de A.Diethe, ~1896 |
 |
| Pintura a óleo do retrato de meio corpo de Caroline Lucretia Herschel, pelo pintor belga Melchior Gommar Tieleman, datada de 1829. A astrônoma tinha 78 anos à época. |
Em 1828, Caroline Herschel é laureada com a Medalha de Ouro[4]
da Sociedade Astronômica de Londres pela catalogação:
[...] de 2.500 nebulosas descobertas por seu ilustre
irmão, o que pode ser considerada a conclusão de uma série de esforços
provavelmente sem paralelo em magnitude ou importância nos anais do trabalho
astronômico.
É eleita membro honorário da Real Academia Astronômica em
1835, e membro honorário da Real Academia Irlandesa em 1838. Em 1846, aos 96
anos, é agraciada com a Medalha de Ouro pela Ciência do rei da Prússia:
Em reconhecimento aos valiosos serviços prestados à astronomia por você, como colega de trabalho de seu irmão imortal, Sir William Herschel, por descobertas, observações e cálculos laboriosos.
[4] Somente em 1996 outra mulher seria laureada com a mesma
honraria: a astrônoma estadunidense Vera Cooper Rubin.
 |
| Sophie Germain, então com 14 anos, por Auguste Eugène Leray |
Nascida em Paris, a maioria de suas fontes afirma que seu pai, Ambroise-François, era um rico comerciante de seda, embora outros acreditem que fosse ourives. Em 1789 foi eleito representante da burguesia naquilo que viria a transformar-se na Assembléia Constitucional, o que leva os biógrafos a supor que Sophie cresceu ouvindo muitas discussões entre seu pai e os amigos sobre política e filosofia. Seja como for, acredita-se que a família permaneceu financeiramente bem o suficiente para sustentar Germain durante toda a sua vida adulta. A queda da Bastilha na França ocorre quando Sophie tinha 13 anos, e a atmosfera revolucionária da cidade obrigou-a a permanecer dentro de casa. Para se divertir, ela procurou a biblioteca de seu pai, onde teve contato com a obra L’Histoire des Mathématiques (A história das matemáticas) do matemático e historiador francês Jean-Étienne Montucla; a curiosa história da morte de Arquimedes ali relatada a intrigou[5]. Sophie concluiu que se o método da geometria, que na época dos gregos englobava toda a matemática pura, pudesse exercer tal fascínio sobre Arquimedes, então esse seria um assunto digno de estudo. Assim, a menina passou a ler cada livro de matemática que encontrou na biblioteca paterna, até mesmo aprendendo latim e grego para conseguir ler obras como as de Isaac Newton e Leonhard Euler. Entre as obras lidas, gostou da Traité d’Arithmétique (Tratado de Aritmética), do matemático francês Étienne Bezout, bem como da Le Calcul Différentiel (O cálculo diferencial), do matemático francês Jacques Antoine-Joseph Cousin. Diz-se que Cousin posteriormente chegou a visitar Germain em sua casa, incentivando-a em seus estudos. Ao descobrirem o fascínio da menina pelo cálculo, seus pais ficaram visivelmente desagradados, uma vez que a matemática era considerada na época inadequada para uma mulher. Diante da insistência de Sophie no prosseguimento de seus estudos, seus pais chegaram a negar-lhe roupas quentes e fogo para o seu quarto, tudo para tentar impedí-la de estudar; porém, assim que saíam do quarto, Sophie pegava velas, enrolava-se em colchas e retomava seus estudos. Depois de um tempo, a própria mãe de Sophie passou a apoiá-la secretamente. Chega o ano de 1794 e com ele a inauguração da Escola Politécnica francesa; Sophie tinha então 18 anos. Como mulher, ela foi impedida de comparecer àquela instituição, mas o novo sistema de educação então vigente tornou as:
“anotações de aula disponíveis a todos os que pedissem”
[5] Arquimedes morreu por volta de 212 a.C. durante a
Segunda Guerra Púnica, quando forças romanas sob o comando do general Marco
Cláudio Marcelo capturaram a cidade de Siracusa após um cerco de dois anos.
Existem diversas versões sobre sua morte. De acordo com o relato dado por
Plutarco, Arquimedes estava contemplando um diagrama matemático quando a cidade
foi capturada. Um soldado romano ordenou que ele fosse conhecer o general
Marcelo, mas ele se recusou, dizendo que tinha que terminar de trabalhar no
problema em que estava entretido. O soldado ficou colérico com a resposta, matando
Arquimedes com sua espada. Plutarco também oferece um relato menos conhecido da
morte de Arquimedes, que sugere que ele possa ter sido morto enquanto tentava
se render a um soldado romano. De acordo com essa versão, Arquimedes estava
carregando instrumentos matemáticos, e foi morto porque o soldado pensou que
fossem itens valiosos. Marcelo teria ficado furioso com a morte de Arquimedes,
visto que o considerava uma posse científica valiosa, e tinha ordenado que o
matemático não fosse ferido. (fonte: https://pt.wikipedia.org/wiki/Arquimedes).
 |
| Selo francês em homenagem a Sophie Germain |
O interesse de Sophie pela teoria dos números seria renovado
após ter lido a monumental obra do matemático alemão Carl Friedrich Gauss, o Disquistiones Arithmeticae (Investigações
Aritméticas). Depois de três anos trabalhando nos exercícios contidos na obra e
tentando suas próprias provas para alguns dos teoremas apresentados, Sophie
escreveu a Gauss (que era um ano mais jovem que ela) – novamente sob o
pseudônimo de M. Le Blanc – em uma carta datada de 21 de novembro de 1804,
apresentando suas considerações sobre o último teorema de Fermat, afirmando
tê-lo provado. Entretanto, sua prova continha uma suposição fraca e, na
resposta, Gauss não tece comentários relativamente à prova apresentada.
Conta-se que por volta de 1807 (durante as guerras napoleônicas) os franceses
ocupavam a cidade alemã de Braunschweig, onde Gauss vivia. Preocupada com a
possibilidade de Gauss vir a sofrer o mesmo destino de Arquimedes, Sophie
escreve ao general Pernety, um amigo da família, solicitando-lhe que garantisse
a segurança do matemático alemão. O general Pernety acede ao pedido dela, enviando
o chefe de um batalhão para conversar com Gauss pessoalmente, e verificar se
ele se encontrava em segurança. No fim das contas, Gauss estava bem, mas ficou
desconcertado com a menção do nome de Germain como responsável por tal
distinção, pois supunha não conhecê-la. Três meses após este incidente, Sophie
revelou a Gauss seu verdadeiro nome (já que se comunicava com ele como M. Le
Blanc), ao que ele lhe respondeu:
Como posso descrever meu espanto e admiração ao ver
meu estimado correspondente M. Le Blanc metamorfoseado nesta pessoa célebre...
quando uma mulher, por causa de seu sexo, nossos costumes e preconceitos,
encontra infinitamente mais obstáculos que os homens para se familiarizar com [problemas
complicados da teoria dos números], mas supera esses grilhões e penetra no que
está mais oculto: ela sem dúvida tem a mais nobre coragem, talento
extraordinário e gênio superior.
Embora Gauss tivesse uma boa e sincera impressão da
competência matemática de Sophie, suas respostas costumavam atrasar-se e ele
geralmente não revisava o trabalho dela. Eventualmente, seus interesses se
afastaram da teoria dos números, e em 1809 as cartas cessaram. Apesar da
amizade entre Germain e Gauss, eles nunca se conheceram pessoalmente. Com o
término da comunicação, Sophie voltou-se para um concurso patrocinado pela
Academia de Ciências de Paris relacionado aos experimentos do físico e músico
alemão Ernst Chladni com placas de metal vibrantes. O objetivo da competição,
conforme anunciado pela Academia, era:
Fornecer a teoria matemática da vibração de uma
superfície elástica e comparar a teoria com evidências experimentais.
Um comentário tecido por Lagrange acerca do concurso,
afirmando que uma solução para o problema proposto exigiria a invenção de um
novo ramo da análise matemática, dissuadiu todos os competidores exceto dois: o
matemático, físico e engenheiro francês Denis Poisson e a própria Sophie
Germain. Uma vez que Poisson acabou eleito pela Academia de Ciências de Paris
para tornar-se juiz do concurso, restou Germain como a única participante dessa
competição. Em 1809 Germain começou a trabalhar, contando com a ajuda de
Legendre, que lhe forneceu suas equações, referências e pesquisas realizadas
até então. A matemática enviou seu artigo em 1811, mas não ganhou o prêmio. A
comissão julgadora considerou que:
As verdadeiras equações do movimento não haviam sido estabelecidas,
embora os experimentos apresentassem resultados engenhosos.
Com a falta de um vencedor, o concurso fora estendido por
mais dois anos e Sophie decide tentar mais uma vez ganhar o prêmio. De início,
Legendre continuou a lhe oferecer apoio, mas depois recusou-se a dar-lhe
qualquer ajuda. Germain submeteu sua proposição anonimamente em 1813, porém a
solução ainda estava repleta de erros matemáticos, o que lhe rendeu somente uma
menção honrosa porque, conforme a comissão:
A base fundamental da teoria [das superfícies
elásticas] não fora estabelecida.
 |
| Mary Sommerville, pintura a óleo de 1834 por Thomas Phillips - Galeria Nacional Escocesa |
 |
| Retrato de Ada Lovelace, pintura a óleo de Margaret Sarah Carpenter, 1836 |
 |
| Sofya Kovaleskaya em foto de 1880 |
 |
Ingrid Daubechies, em 2005 |
 |
| À esquerda: Mary Winston Jackson; à direita: Gladys West |
 |
A matemática e professora Maryam Mirzakhani |
É certo afirmar que estaremos sendo, até certo ponto,
injustos com inúmeras outras matemáticas com merecido destaque na ciência dos
números ao não citá-las nominalmente, mas o objetivo deste singelo capítulo foi
o de apresentar algumas biografias, cujos pensamentos abstratos singulares e
histórias de vida – temperadas com alegrias e tragédias – mostram a força, a
dignidade, e a competência das mulheres em todas as áreas do conhecimento, em
todos os tempos.
Apêndice – Cartas de Sinésio a Hipátia:
Complementando este capítulo, e por se tratar de um material
muito antigo que conseguiu sobreviver até os nossos dias, seguem abaixo as sete
cartas atribuídas ao bispo grego de Ptolemaida, Sinésio de Cirene, encaminhadas
à sua ex-professora, a filósofa grega Hipátia de Alexandria.
Carta 154: De seus
próprios escritos
Em que Sinésio discute
– entre outras coisas – seu papel frente a sofistas e filósofos, pedindo a
Hipátia que dê o seu parecer acerca das duas obras de sua autoria, a ela
encaminhadas: “Dio” e “Dos sonhos”.
[1] À filósofa,
Trouxe dois livros este ano. Um deles porque fui
movido para lá pelo próprio Deus, o outro por causa da calúnia dos homens.
[2] Alguns daqueles que vestem o manto branco ou
escuro afirmam que sou infiel à filosofia, aparentemente porque professo graça
e harmonia de estilo, e porque me atrevo a dizer algo sobre Homero e sobre as
figuras dos retóricos. Aos olhos de tais pessoas, deve-se odiar a literatura
para ser um filósofo e deve-se ocupar apenas com assuntos divinos. Sem dúvida,
esses homens sozinhos tornaram-se espectadores do cognoscível. Este privilégio
é ilícito para mim, pois gasto parte do meu lazer purificando minha língua e
adoçando meu humor.
[3] O que os incitou a me condenar, sob a acusação de
que sou digno apenas de ninharias, é o fato de que minha “Cinegética” [uma obra
sobre a criação de cães] desapareceu de minha casa, como eu não sei, e foi
recebida com grande entusiasmo por alguns jovens homens que cultuam aticismos e
períodos graciosos. Além disso, algumas tentativas poéticas minhas pareceram-lhes
obra de um artista que reproduz a antiguidade, como costumamos dizer quando
falamos de estátuas.
[4] Há certos homens entre meus críticos cujo
descaramento só é superado por sua ignorância, e esses são os mais dispostos entre
todos a desenrolar discussões a respeito de Deus. Sempre que os encontras, te
vês obrigado a ouvir sua tagarelice sobre silogismos inconclusivos. Derramam
uma torrente de frases sobre aqueles que não precisam delas, nas quais, suponho,
encontram seu próprio proveito. Os professores públicos, que se vêem em nossas
cidades, vêm desta classe. É mesmo um Chifre de Amalthea [o “chifre da
abundância” do mito grego] que se consideram no direito de usar. Irás, creio eu,
reconhecer esta tribo maleável, erroneamente chamada de nobreza de propósito. Desejam
que eu me torne seu pupilo; dizem que em pouco tempo me farão todo ousado nas
questões da divindade e que poderei declamar dia e noite sem parar.
[5] Os demais, que têm mais gosto, são sofistas, muito
mais infortunados que estes. Gostariam de ser famosos da mesma maneira, mas – infelizmente
para eles – são incapazes até mesmo disso. Conheces alguns que, espoliados pelo
escritório do coletor de impostos, ou instado a isso por alguma calamidade,
tornaram-se filósofos no meio de suas vidas. Sua filosofia consiste em uma
fórmula muito simples: invocar a Deus para testemunhar, como fez Platão, sempre
que negam alguma coisa ou sempre que afirmam alguma coisa. Uma sombra ultrapassaria
esses homens ao proferirem algo de pertinente; mas suas pretensões são
extraordinárias. Oh, que sobrancelhas orgulhosamente arqueadas! Eles sustentam
suas barbas com a mão. Assumem um semblante mais solene que as estátuas de
Xenócrates. Estão até decididos a nos agrilhoar a uma lei que lhes é totalmente
vantajosa: a saber, que ninguém terá a posse desobstruída de qualquer
conhecimento do bem. Julgam isto uma revelação de si mesmos se qualquer um, assim
considerado filósofo, souber como falar, pois crêem esconder-se atrás de um véu
de simulação e de parecerem-se bastante cheios de sabedoria por dentro.
[6] Estes são os dois tipos de homens que falsamente
me acusaram de ocupar-me em atividades triviais; um deles porque não falo o
mesmo tipo de besteiras que eles, o outro porque não mantenho minha boca
fechada, e não mantenho o 'touro na minha língua', como eles. Contra esses foi
composto meu tratado, que lida com a loquacidade de uma escola e com o silêncio
da outra. Embora seja esta última em particular a quem se dirija, nomeadamente
aos homens mudos e invejosos em questão (não pensas tu neles com alguma graça?),
não obstante, ela encontrou meios de arrastar também aqueles outros homens, e
pretende ser não menos uma exposição e mais um elogio de grande aprendizagem.
Nem abjurei de suas acusações, e para sua ainda maior frustração, muitas vezes
os cortejei.
[7] A seguir, passando quanto à escolha de uma vida, o
trabalho de louvores daquela filosofia como a mais filosófica das escolhas; e
que tipo de escolha deve ser considerado, aprende-se com o próprio livro. Finalmente,
ele defende também minha biblioteca, que os mesmos homens acusaram, sob o
fundamento de que oculta cópias não revisadas. Esses camaradas malvados não
afastaram suas mãos nem mesmo de coisas como essas. Se cada coisa está em seu
devido lugar; e todas as coisas foram tratadas a tempo; se os motivos por trás
de cada parte do empreendimento são justos; se ele foi dividido em vários
capítulos do mesmo modo que na obra divina “Fédon”, em que Platão discute os
vários tipos de belo; se todos os argumentos foram concebidos para convergir
para o fim proposto; se, além disso, a convicção veio silenciosamente de qualquer
lugar para apoiar a monotonia da narrativa, e se por convicção resultou uma
demonstração, como acontece em tais casos, e se uma coisa segue a outra
logicamente, esses resultados têm de ser dádivas da natureza e da arte.
[8] Aquele que não é indisciplinado para descobrir até
mesmo um certo semblante divino oculto sob um modelo mais grosseiro, como
aquela Afrodite, ou aquelas Graças, e tais divindades encantadoras como aquelas
que os artistas atenienses ocultaram dentro das figuras esculpidas de um Sileno
ou de um Sátiro, esse homem, em todos os eventos, apreenderá tudo o que meu
livro desvelou dos dogmas místicos. Mas tais significados escaparão facilmente aos
outros por causa de sua semelhança à redundância e aparentarem ter sido jogados
na narrativa muito por acaso, e quão grosseiramente podem aparentar. Os
epilépticos são as únicas pessoas que sentem as influências frias da lua. Por
outro lado, apenas àqueles que recebem os lampejos das emanações do intelecto,
na plena saúde dos olhos da mente, Deus acende uma luz semelhante à sua, aquela
luz que é a causa do conhecimento para o intelectual e, às coisas conhecíveis,
a causa de serem conhecidas. Da mesma forma, a luz comum conecta a visão com a cor.
Mas remova essa luz, e seu poder de discernir é ineficaz.
[9] Quanto a tudo isso, aguardarei sua decisão. Se
decretares que devo publicar meu livro, dedicá-lo-ei a oradores e filósofos
juntos. Aos primeiros agradará, e aos outros será útil, desde que, claro, não
sejam rejeitados por você, quem é realmente apta a dar julgamento. Se ele não
lhe parecer digno de ouvidos gregos, se, como Aristóteles, valorizas mais a
verdade que a amizade, uma escuridão próxima e profunda o obscurecerá, e a
humanidade jamais ouvirá sê-lo mencionado.
Muito sobre este assunto [já foi falado].
[10] A outra obra [Dos sonhos] Deus ordenou e deu Sua
sanção a ela, e foi criada como uma oferta de gratidão às faculdades
imaginativas. Contém uma investigação de toda a alma imaginativa e de alguns
outros pontos que ainda não foram tratados por nenhum filósofo grego. Mas por
que alguém deveria alongar-se com isso? Este trabalho foi concluído, todo ele,
em uma única noite, ou melhor, no final de uma noite, uma que também me trouxe
a visão recomendando-me escrevê-lo. Há duas ou três passagens no livro em que eu
parecia ser outra pessoa, e ouvia a mim mesmo entre os outros que estavam presentes.
[11] Mesmo agora esta obra, sempre que a examino,
produz sobre mim um efeito maravilhoso, e certa voz divina me envolve como na
poesia. Se esta minha experiência não é única, ou ocorra a outro, acima disso tudo
tu me iluminarás, pois depois de mim serás a primeira entre os gregos a ter
acesso à obra.
[12] Os livros que envio a ti ainda não foram
publicados e, para que o número esteja completo, envio também meu ensaio sobre a
Dádiva. Isso foi produzido há muito tempo, em meu período como embaixador. Foi
dirigido a um homem que teve grande influência sobre o imperador e Pentápolis
lucrou um pouco com o ensaio e também com a prenda.
Carta 124: Uma cidade
em tempos de guerra
Em que Sinésio lamenta
os graves problemas que afligem sua cidade. Carta escrita por volta de 401
d.C., ainda que uma data situada entre 411–412 também seja aceitável.
[1] À filósofa,
Mesmo que
haja completo esquecimento dos mortos no Hades, mesmo
lá eu me lembrarei de ti*
minha querida Hipátia. Estou cercado pelos sofrimentos
de minha cidade e desgostoso com ela, pois diariamente vejo as forças inimigas
e os homens massacrados como vítimas em um altar. Estou respirando um ar
contaminado pela decomposição de cadáveres. Aguardo para submeter-me à mesma
sorte que se abateu sobre tantos outros, pois como manter a esperança, quando o
céu está obscurecido pelas sombras das aves de rapina?
[2] No entanto, mesmo nessas condições, eu amo o país.
Por que então eu sofro? Porque sou líbio, porque nasci aqui, e é aqui que vejo
os honoráveis túmulos dos meus antepassados. Só por tua causa, acho que seria
capaz de ignorar minha cidade e mudar minha morada, se algum dia tivesse a
chance de fazê-lo.
* [Homero, Ilíada 22:389]
Carta 33: Em louvor
de Alexandre
Carta escrita em 394
d.C., conteúdo incompleto
[1] À filósofa,
Eu parecia destinado a desempenhar o papel de eco. Quaisquer
que sejam os sons que ouço, eu os repito. Transmito-te agora os elogios do
maravilhoso Alexandre1…
1 Talvez um parente de Sinésio
Carta 15: Um
densímetro
Carta escrita em 402
d.C., é a primeira descrição no mundo de um densímetro ou hidrômetro. A
descrição de Sinésio é bastante acurada. A maneira como um densímetro funciona
está baseado em um famoso princípio de Arquimedes, descrito em sua obra “Dos
corpos flutuantes”: “Qualquer objeto, total ou parcialmente imerso em um fluido,
é impulsionado por uma força igual ao peso do fluido deslocado pelo objeto”.
[1] À Filósofa,
Estou tão mal afortunado que necessito de um densímetro.
Cuide para que seja moldado em latão e montado para mim.
[2] O instrumento em questão é um tubo cilíndrico,
que tem a forma de uma flauta e possui aproximadamente o mesmo tamanho. Possui
entalhes em uma linha perpendicular, por meio dos quais podemos testar o peso
das águas. Um cone forma uma tampa em uma das extremidades, bem ajustada ao
tubo. O cone e o tubo possuem apenas uma base. Esta é chamada de barílio.
Sempre que colocares o tubo em um líquido, ele permanecerá ereto. Podes então
contar os entalhes à vontade e, desta forma, determinares a gravidade
específica da água.
Carta 16: Uma
despedida
Uma das últimas cartas
conhecidas de Sinésio.
[1] À Filósofa,
Estou ditando esta carta a ti de minha cama, mas que a
recebas com boa saúde, mãe, irmã, professora e, além disso, benfeitora, e tudo
o que for honrado em nomes e ações.
[2] Para mim, a fraqueza corporal seguiu-se ao
sofrimento mental. A lembrança de meus filhos falecidos está consumindo minhas
forças pouco a pouco. Só por tanto tempo deveria ter vivido Sinésio, uma vez
que ainda estava sem experiência dos males da vida. É como se uma torrente há muito
reprimida tivesse explodido sobre mim em todo o seu volume, e como se a doçura
da vida tivesse desaparecido. Que eu deixe de viver ou de pensar no túmulo de
meus filhos!
[3] Mas que preserves tua saúde e dês minhas
saudações a cada um de teus felizes camaradas, começando pelo pai Teotecno e
irmão Atanásio, e assim a todos! E se alguém foi adicionado a estes, desde que
seja querido para você, devo-lhe gratidão, pois que é estimado por ti, e a este
homem apresento minhas saudações como a meu próprio amigo mais querido. Se quaisquer
de meus negócios lhe interessam, faça bom uso, e se nenhum deles lhe interessar,
tampouco interessam a mim.
Carta 10: Perdendo
contato com o mundo exterior
Carta em tom de
desespero, escrita em 413 d.C., quando Sinésio enfrentava graves problemas por
ter tido um conflito com o governador Andrônico.
[1] À Filósofa,
Eu te saúdo e peço-te que saúdas por mim aos teus
mais felizes camaradas, augusta Senhora. Há muito tempo venho censurando-te por
não ser considerado digno de uma carta, mas agora sei que sou desprezado por
todos vocês por não ter feito nada de errado de minha parte, mas porque sou
infeliz em muitas coisas, em tantas quantas um homem pode ser.
[2] Se eu pudesse ter recebido cartas de ti e sabido
como estão todos vocês – tenho a certeza de que estão felizes e desfrutando de
boa sorte - teria ficado aliviado, nesse caso, de metade dos meus próprios
problemas, de regozijo por sua felicidade. Mas agora o teu silêncio foi
adicionado à soma das minhas tristezas.
[3] Perdi meus filhos, meus amigos e a boa vontade de
todos. A maior perda de todas, entretanto, é a ausência de teu divino espírito.
Tinha a expectativa de que isso permaneceria sempre para mim, para vencer os
caprichos da fortuna e as reviravoltas malignas do destino.
Referências bibliográficas:
|
[1] |
Mark, J. J. “Alexandria”, Ancient History Encyclopedia, April 2011.
Link de acesso: |
|
[2] |
McLemore, E. W. “Past-present (We) – Present-future (You)”,
Association for Women in Mathematics, Volume 9, Number 6, Nov-Dec 1979. |
|
[3] |
Deaking, M. A. B. “Hypatia and her mathematics”, The American
Mathematical Monthly, March 1994, volume 101, No. 3, pp 234-243. |
|
[4] |
Adair, G. “Hypatia”, Agnes Scott College, Class of 1998. Link de acesso: |
|
[5] |
Riddle, L. “Theano”, Agnes Scott College, 2017. Link de acesso: |
|
[6] |
Platão, “Êutifron, Apologia
de Sócrates, Críton”, tradução, introdução e notas de José Trindade Santos,
Imprensa Nacional – Casa da Moeda, 4ª edição, 1983. |
|
[7] |
Waithe, M. E. “A history of women philosophers – Volume I: Ancient
women philosophers (600 B.C. – 500 A.D.)”, Martinus Nijhoff Publishers, 1992.
ISBN: 978-90-247-3368-2, e-ISBN: 978-94-009-3497-9. |
|
[8] |
Gandersheim, R. “The plays of Roswitha”, tradução de Christopher St.
John para o inglês, Project Gutenberg, June/2019. |
|
[9] |
Wheeler, B. (editor) “Listening to Heloise: The voice of a twelfth-century
woman”, Palgrave Macmillan, 2000. ISBN: 978-1-349-61876-7, ISBN-e:
978-1-349-61874-3. |
|
[10] |
McLaughin, M. M.; Wheeler, B. “The letters of Heloise and Abelard – A
translation of their collected correspondence and related writings”, Palgrave
Macmillan, 2009. ISBN: 978–0–312–22935–1 |
|
[11] |
Thieling, S. “Elena Lucrezia Cornaro Piscopia”, Agnes Scott College,
Class of 1999. Link de acesso: https://www.agnesscott.edu/lriddle/women/piscopia.htm |
|
[12] |
Wikipedia, “Elena Cornaro
Piscopia”. Acessado em Janeiro/2021. Link de acesso: |
|
[13] |
Mandic, S. “Emilie du Châtelet”, Agnes Scott College, Class of 1997. Link de acesso: https://www.agnesscott.edu/lriddle/women/chatelet.htm |
|
[14] |
Wikipedia, “Émilie du
Châtelet”, acessado em Janeiro/2021. Link de acesso: |
|
[15] |
du Châtelet, “Dissertation sur la nature et la propagation du feu”,
1737. |
|
[16] |
Hamel, F. “An eighteenth-century marquise: A study of Emilie du
Châtelet and her times”, Stanley Paul & Co., 1910. |
|
[17] |
Strick, H. K. “Maria Gaetana Agnesi”, Spektrum der Wissenschaft
Verlagsgesellschaft Heidelberg, 2018. |
|
[18] |
Dumbaugh, D. “Maria Gaetana Agnesi (1718 – 1799)”, Notices of the American
Mathematical Society, Volume 6, Number 3, March 2019. |
|
[19] |
Mazzotti, M. “Maria Gaetana Agnesi: Mathematics and the making of the
catholic enlightment”, Isis, Volume 92, Number 4, December 2001. |
|
[20] |
Gaetana, M. “Instituzione
Analitiche ad uso della gioventu italiana”, 1748. |
|
[21] |
Gaetana, M. “Propositiones
Philosophicae”, 1738. |
|
[22] |
Wikipedia, “Caroline
Herschel”, acessado em Março/2021. Link de acesso: |
|
[23] |
Nysewander, M. “Caroline Herschel”, Agnes Scott College, Class of
1998. Acesso em Março/2021. https://www.agnesscott.edu/lriddle/women/herschel.htm |
|
[24] |
Wikipedia, “Sophie Germain”,
https://en.wikipedia.org/wiki/Sophie_Germain, acessado em Março/2021. |
|
[25] |
Swift, A. “Sophie Germain”, Agnes Scott College, Class of 1995. Acessado em Março/2021. https://www.agnesscott.edu/lriddle/women/germain.htm |
|
[26] |
Hill, A. M. “Sophie Germain: A mathematical biography”, Bachelor of
Arts thesis, Department of Mathematics and the Honors College of the
University of Oregon, August 1995. |
|
[27] |
Germain, S. “Recherches sur la théorie des surface élastiques”, 1821. |
|
[28] |
O’Connor, J. J.; Robertson, E. F. “Mary Fairfax Greig Somerville”, MacTutor.
https://mathshistory.st-andrews.ac.uk/Biographies/Somerville/. Março/2021. |
|
[29] |
Wood, S. “Mary Fairfax Somerville”, Agnes Scott College, Class of
1997. Acessado em Março/2021. https://www.agnesscott.edu/lriddle/women/somer.htm |
|
[30] |
Sommerville, M. F. “Mechanism of the heavens”, John Murray,
Albermale-Street, London, 1831. |
|
[31] |
Sommerville, M. F. “Physical Geography”, John Murray,
Albermale-Street, London, 1851. |
|
[32] |
Toole, B. “Ada Byron, Lady Lovelace”, Biographies of women mathematicians,
Agnes Scott College. https://www.agnesscott.edu/lriddle/women/love.htm. Acessado em Março/2021. |
|
[33] |
Wikipedia, “Ada Lovelace”, https://en.wikipedia.org/wiki/Ada_Lovelace. Acessado em Março/2021. |
|
[34] |
O’Connor, J. J.; Robertson,
E. F. “Sofia Vasilyevna Kovalevskaya”, MacTutor. https://mathshistory.st-andrews.ac.uk/Biographies/Kovalevskaya/. Mar/2021. |
|
[35] |
Wilson, B. “Sofia Kovalevskaya”, Agnes Scott College, Class of 1997. Acessado em Março/2021. https://www.agnesscott.edu/lriddle/women/kova.htm |
|
[36] |
O’Connor, J. J.; Robertson, E. F. “Ingrid Daubechies”, MacTutor.
Março/2021. https://mathshistory.st-andrews.ac.uk/Biographies/Daubechies/. |
|
[37] |
Riddle, L. “Ingrid Daubechies”, Agnes Scott College. Acessado em Março/2021. https://www.agnesscott.edu/Lriddle/women/daub.htm |
|
[38] |
Shetterly, M. L. “Mary W. Jackson Biography”, acessado em Abril/2021.
Link: |
|
[39] |
Wikipedia, “Gladys West”,
acessado em Abril/2021. Link de acesso: |
|
[40] |
O’Connor, J. J.; Robertson, E. F. “Maryam Mirzakhani”, MacTutor.
Aril/2021. https://mathshistory.st-andrews.ac.uk/Biographies/Mirzakhani/ |
|
[41] |
Livius.org, “Synesius
letters”, acessado em Janeiro/2021. Link de acesso: |
|
[42] |
Costa, M. R. N.; Costa, R.
F. “Mulheres intelectuais na idade média: entre a medicina, a história, a
poesia, a dramaturgia, a filosofia, a teologia e a mística”, Editora Fi,
2019. ISBN: 978-85-5696-599-8 |
Esta postagem é parte integrante do e-book gratuito Matemática: Uma abordagem histórica - Volume 2. Caso queira obter um exemplar, clique aqui.